摘要:新课标指明，情境是学生进行数学思考、解决问题的环境。有效的教学情境，可以在调动学生学习兴趣的同时，让学生积极思考、解决问题，从而达到掌握数学知识，发展核心素养，实现数学学习提质减负的目标。基于此，本文主要论述在“双减”背景下，教师可以在新课标的指引下，关注情境教学，尤其以数学课堂为依托，遵循适宜原则，使用合理策略，创设教学情境，实现其价值，促使学生获得良好发展。

　　［关键词］初中数学,课堂情境,核心素养,新课标,创设策略

　　当前，数学教学改革正处在“双减”的关键时期。教师需要将学生置于教学的核心位置，对传统的教学方法进行创新和改进。教师应该鼓励学生主动思考、积极探索，使他们在掌握数学知识和方法的同时，也能够培养和发展自己的核心素养。这样的教学方式不仅能够提高学生的学习效果，还能够有效地减轻学生的课业负担和校外培训的压力。因此，引发学生的思考和探究是提高数学学习质量、减轻学生负担的关键。根据《义务教育数学课程标准（2022年版）》（以下简称“新课标”）的要求，教师在选择教学方法时，应注重情境设计和问题提出，以激发学生的主动参与和思考。这样，学生在进行学习的过程中，可以更好地进行数学思考、表达和应用，从而更有效地掌握知识，解决问题，培养思维能力，并逐步发展其数学核心素养。

　　一、初中数学课堂情境的创设原则

　　有效创设教学情境，离不开适宜的原则。不同的创设原则会产生不同的创设方法。一般情况下，在创设数学课堂情境时，教师可遵循如下原则。

　　（一）生活性原则

　　新课标强调创设真实情境。创设真实情境可以从社会生活、科学和学生已有数学经验等方面入手，依据教学内容，选择贴近实际的素材进行加工。基于此，教师可以遵循生活性原则创设数学课堂情境。

　　例如，销售问题是数学学科的重要内容，亦是大部分学生难以理解的问题。这是因为学生缺少销售经历，不理解“售价”“标价”“利润”“利润率”等概念。实际上，部分学生在体验生活时，都曾有过购物经验，在一定程度上对“售价”“标价”“利润”“利润率”等概念有了感性认知。而感性认知是学生深入探究的支撑，所以在课堂上，教师可以组建合作学习小组，让每组成员迁移生活经验，各自扮演顾客和商人角色，创设商品交易的场景。在此过程中，碰上有学生讨价还价时，教师可以趁机融入“售价”“标价”等概念，同时鼓励学生计算，判断降价后是否赢利。在体验情境时，学生学会迁移生活经验，具体问题具体分析，以认真运算来解决即时遇到的问题，由此轻松地建立数学认知，丰富生活经验，学会用数学的方法来解决现实生活问题。

　　（二）趣味性原则

　　心理学研究表明，轻松愉快的情感体验，可以让学习者产生学习兴趣。

　　在学习兴趣的助力下，学习者可以轻松地获取知识、技能和经验等。趣味教学，是学生进行轻松愉快感体验的支撑。所以，教师可以遵循趣味性原则创设课堂教学情境。

　　例如，在“平面直角坐标系”这节课上，教师可以随机请两位学生起立，然后让其他学生观察他们的位置，试着进行描述。在描述时，大部分学生可能会尝试使用方位法。但是，由于知识有限，无法用方位法准确地描述出两个学生所处的位置。此时，部分学生产生好奇心，想要知道准确描述位置的方法。趁学生的求知欲旺盛，教师这时可以在交互式电子白板上出示棋盘，提出规则—请将棋盘想象成平面直角坐标系，利用坐标描述其上不同棋子所在位置。学生听到这里，便开始开动脑筋，试着将棋盘转化为平面直角坐标系，确定原点、x轴、y轴，用数对描述棋子的位置。这时，教师可依据学生描述的情况，并结合教学内容，提出平面直角坐标系中如何确定点的位置相关问题，促使学生进行探究，在教师的引导之下不断解决问题。这样，学生在充满趣味的学习情境中不断探究并解决问题，从而一步步地掌握所学知识内容，增强课堂学习效果。

　　（三）启发性原则

　　教学情境的作用之一是引发学生思考，解决问题。有效的教学情境具有启发性，可以使学生受到启迪，一步步地解决问题，得出结论，从而达到深刻理解数学知识，发展学生核心素养的目标。因此，在教学实践中，教师可以遵循启发性原则创设教学情境。

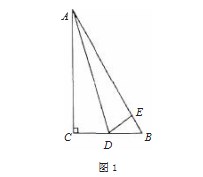
　　例如，在“勾股定理”这堂课上，教师先引导学生探究勾股定理。在学生建立一定的认知后，教师可以创设问题情境。比如，在教学过程中，教师在交互式电子白板上呈现图像（见图1）：同时描述问题：“△ABC是直角三角形。其中，AC=4，BC=3。沿着AD进行折叠，使AC与AE重合。请问，CD有多长？”因接受数学知识有限，有一部分学生可能会遭遇解题阻碍。为使他们顺利地解决问题，教师可再进行进一步引导：“根据AC=4，BC=3，可以求出哪些线段的长度？”有学生运用勾股定理，计算出AB的长度、BE的长度。教师追问“倘若CD=x，可以用含x的代数式表示哪些线段的长度？”学生再次阅读题目，观察图像，联想勾股定理的相关内容，确定DE=CD=x，并借助和差关系，列出等式：BD=BC-CD=3-x。教师接着发问：“如何计算出CD的长度？”学生继续联想勾股定理的相关内容，列出方程，认真运算，从而得到x的值，即CD的长度。在问题情境中，学生受到一个个问题的启发，逐步剖析已知条件，迁移课堂认知，运用已学知识，厘清问题解决思路，解决问题。如此，学生不但加深了对勾股定理的理解，还锻炼了运算能力、数学应用能力，有利于提升学生核心素养发展水平。

　　（四）现代性原则

　　新课标要求教师紧密结合数学教学与信息技术，增强教学趣味性和有效性。教师可以遵循现代性原则，应用现代信息技术创设教学情境。现代信息技术可以直观、动态地展现数学内容，容易引发学生兴趣。学生可以在轻松有趣的学习环境中，积极发散思维，自觉地进行数学抽象和数学推理等，以此达到探寻数学思想方法，掌握数学知识的目的。

　　二、初中数学课堂情境的创设策略

　　教学有法，教无定法。在遵循如上创设原则的同时，教师可以结合自身教学经验，根据教学内容，在课堂导入、课堂讲解、课堂总结环节使用不同策略，创设课堂情境，让学生进行体验和探究，以此增强课堂学习效果。解决能力，一举两得，有利于提高课堂学习质量。

　　（二）课堂讲解情境的创设策略

　　课堂讲解环节重在引导学生探究、解决问题。解决问题的方式有很多，如自主解决、合作解决等。在课堂讲解环节，教师可以依据教学内容和学生学习情况，选择不同的问题解决方式，以此为基础创设课堂情境，给学生提供问题解决机会。

　　例如，在“综合运用—一元二次方程解法”这节课之前，学生们体验了多样的教学活动，逐步掌握了配方法、因式分解法等。在这堂课上，教师准备引导学生综合运用不同的方法，解答一元二次方程。在课堂讲解环节，教师可以黑板上呈现一个题目：x2+2x-3=0。同时，教师鼓励学生与小组成员合作，共享不同的方法。在两分钟后，统计各组的方法，方法数量多且正确的一组为获胜方。在竞争意识的驱动下，各组学生积极性高涨，积极思考，探索不同的解题方法，认真运算，并与小组成员共享不同的方法，互相汲取经验和方法。

　　在规定的时间结束后，大部分小组总结出了三种方法—配方法、公式法、因式分解法。于是，教师可以鼓励小组毛遂自荐，当堂演示不同的解题方法。如“配方法：移动常数项，得到x2+2x=3。等式两边同时加1，构成完全平方式，得到x2+2x+1=4。因式分解得到（x+1）2=4。运算得出结果：x1=-3，x2=1”。

　　在学生代表呈现不同方法后，教师接着可以发问：“这些方法是否都可以用来解答任何一元二次方程？”学生主动与小组成员交流。在交流时，有小组成员可能很快就联想到不同的一元二次方程，从而进行求解，由此得出结论—可以用配方法和因式分解法解答任何一元二次方程，只能用因式分解法解答部分一元二次方程。其他学生在倾听时，提出问题：在什么情况下，可以用因式分解法解答一元二次方程？然后学生代表就可以描述一元二次方程特征，列出相关方程并认真解答。

　　在这样的合作情境中，学生不断地发现问题和着手解决问题，从而达到查漏补缺、深层探究的效果。

　　（三）课堂总结情境的创设策略

　　课堂总结是学生梳理知识、强化认知的环节。学生梳理知识的方法有很多，如总结归纳法、知识延伸法、对比异同法等。在数学课堂总结环节，教师可以依据课堂教学内容和学生学习情况，选择适宜的总结方法，就此创设情境，让学生在总结环节进行知识的梳理。

　　以对比异同法为例，此法是指对比相似知识点的相同点和不同点，加深认知。比如，在学习“菱形”时，学生可通过体验多种活动来探究菱形的概念、性质等。但是，在这个过程中，也不乏学生混淆了菱形和矩形。针对此情况，在课堂总结环节，教师要先鼓励学生回顾本节课所学，描述菱形的概念和性质。有部分学生能准确地进行描述。教师把握时机，追问：“矩形的概念和性质是什么？”全体学生进行头脑风暴，联想、描述矩形的概念和性质。在学生描述后，教师发问：“矩形和菱形有哪些相似之处？有哪些不同之处？”在问题的作用下，学生就了解了矩形和菱形的概念及其性质，然后会尝试区分它们之间的相似和不同之处。有学生提道：“从定义上看，菱形和矩形都是平行四边形。不同点是，矩形有一个角是直角。”也有学生提道：“从性质上看，矩形和菱形的对边平行且相等，对角相等、邻角互补，对角线互相平分。不同点是，矩形的对角线相等，四个角是直角；菱形的对角线垂直，四边相等。”在学生描述之际，教师使用交互式电子白板画出矩形和菱形，并重点标注相关内容，帮助其他学生建立直观认知。总的来说，在当前的“双减”政策背景下，教师需要在新课标的指导下，深入探讨课堂情境对学生学习的影响，结合教学内容，遵循生活性原则、趣味性原则、启发性原则和现代性原则，紧扣不同的教学环节，运用多种策略，创设不同的课堂情境，以激发学生的学习兴趣。通过这种方式，学生可以积极思考，主动解决问题，从而由浅入深地建立数学认知，掌握数学思想方法，发展核心素养。

参考文献：

　　[1]章倩倩.初中数学课堂情境创设的原则与策略研究[D].上海：华中师范大学,2022.

　　[2]池至楠.基于核心素养下初中数学课堂情境创设策略探究[J].考试周刊,2021(59):62-63.

　　[3]王转宁.情境创设在初中数学课堂中的应用研究[J].智力,2021(19):169-170.

　　[4]赵冬星.新背景下初中数学课堂教学中情境创设研究[J].新课程,2020(45):51.

　　[5]高同桥.一样课堂,别样精彩—初中数学情境创设策略探究[J].才智,2020(11):132.