摘 要 : 在初中数学教学的过程中教师要遵循“双减”政策，切实减轻学生的作业负担，促进学 生的身心发展.其实要真正落实“双减”政策，教师不仅要减少学生作业的量，同时要提升课堂的质 量.学生只有在课上多学了，在课后的负担才能真正地减少.教师在课堂巧设支架，能促进学生思维 的发展，提升学习效率，进而在课堂上发展他们的学科素养.

　　关键词 : 多元支架,初中数学,m双减政策

　　“双减”政策表面上针对的是课后作业设置，本 质上是要求教师提升学生的学习能力，提高课堂教 学效率.因此在课堂教学中，教师要以学生为主，让 学生多思考，多展示，要让学生成为课堂的主人.教 师的作用在于在学生展示的过程中，给学生创设不 同的支架，推动学生前行.建构支架不是越俎代庖， 而是给学生及时地帮助，让学生更有信心、更有思路 去思考，最终提升创造能力与迁移应用能力.

　　1 建构情境支架，引领学生转换思维

　　初中数学的大多内容以抽象思维为主，但初中 学生的思维方式还以形象思维为主.部分学生遇到 不会解决的问题，往往是因为不能将抽象问题转化 为更直观地形象化问题.因此在教学的过程中教师 可建构情境支架，以让学生在熟悉的情境中思考问 题，进而迸发出思维的火花.教师建构的情境支架要 紧扣涉及的问题，让学生借助情境自然而有深度地 思考原先的问题.教师创设的情境要基于学生的生 活，要能吸引学生的关注，引发学生探究的热情.

　　案例 1 在学习“等边三角形”时，教师设置如 下问题 : 已知 AD 是ΔABC 的中线，∠ADC = 60 ° , BC= 4.把ΔADC 沿直线 AD 折叠后，点 C 落在点 C' 的 位置上，求 BC'的长.

　　本题没有直接给出图形，让学生根据已知条件 求线段 BC' 的长.对学生而言，让他们从抽象的条件 中思考解题思路是有一定难度的.因此教师可帮助 学生建构情境支架，让学生更直观地思考问题.教师 让学生用一张纸片折叠出ΔABC.在折叠时，要使线 段 BC 的长为4.同时要使点 D 为 BC 的中点，∠ADC = 60 ° . 在学生完成这一步操作之后，教师再引导学 生按照题目的要求进行再次折叠，学生把ΔADC 沿 直线 AD 折叠后，点 C 自然地落在一个新的位置上， 将其记作点 C'.学生用直尺测量出线段 BC 和线段 BC'的长，易发现 BC' 的长是 BC 长的一半.有了这 样直观的体验，学生就能很轻松地将折叠过程画成 图形，如图 1 所示.对照图形，学生就很容易发现所 求线段与已知条件的逻辑关系.如图 2.连接 BC'，因 为 AD 是 ΔABC 的 中 线，所 以 BD = DC.又 DC = DC'，所以 BD = DC'.因为∠ADC = 60 ° , 所以∠ADC' = 60 ° , 从而可得∠BDC' = 60 ° , 所以 ΔBDC'是等边 三角形.由此可知 BC' = BD = 2.

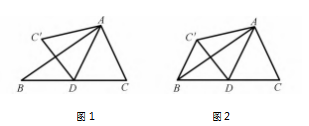
　　在解决本题的过程中，教师为学生创设了直观的情境支架，先是让学生按照已知条件进行折叠操 作，进而猜测出结论.接着在教师的帮助下，学生画 出具体的图形，在数形结合中，学生最终获得了问题 的求解方法.从解题过程可以看出，建构情境支架更 容易引发学生思维的火花.

　　2 建构问题支架，促进学生深化思维

　　在数学教学过程中，教师可创设问题支架，引发 学生进一步思考.教师设定的问题支架能给学生指 定思考的方向，进而更好地聚焦他们的思维.

　　案例2 在学习“直线与圆的位置关系”时，教师 可设定这样的题目: 如图 3.

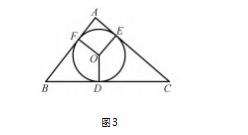
       已知⊙O 内切于ΔABC，切 点分别为 D，E，F，且 AB = 9 cm，BC = 14 cm，CA = 13 cm.请根据已知条件提出一个问题，并给出解答.根据图形特征，学生首先想到的就是切线长定 理，即由“⊙O 内切于 ΔABC”这一条件得 出 AF = AE，BF = BD，DC = CE.由此学生思考能不能借助这 些等量关系求出线段 AF，或者线段 BD，或者线段 CE 的长.学生发现求某条线段的长有一定的困难， 因此有放弃求解的念头.此时，教师可给出这样的问 题支架 : 请同学们思考，能不能同时求得三条线段的 长? 根据教师的提示，学生易想到利用三元一次方 程组求解.学生尝试着设 AF = x，BD = y，CE = z，于 是 AE = AF = x，BF = BD = y，CD = CE = z.因为 AB = 9 cm，BC = 14 cm，CA = 13 cm，从而得 出方程组

　　由此可见，在“双减”背景下，教师要给学生更 多展示的机会，要给学生更多思考的时间.只要学生 养成良好的思考习惯，学生解决问题的能力就提高 了，课后作业负担自然就降低了.借助问题支架，教 师可培养学生思维的广度与深度.

　　3 建构合作支架，引导学生拓展思维

　　基于“双减”政策，教师需要给学生更多 自主 的空间，减少学生课后作业其实就是让学生更自 主地学习，更自由地支配课后的时间.在课后遇 到问题时，学生有充足的时间来解决问题，学生 的负担尤其是心理负担也会自然降低.教师可让 学生在课后通过合作，依靠团队的力量去解决问 题.因此教师需要在课堂上培养学生合作学习的 能力，发挥他们 的潜力，让他们能在课后游刃有 余地面对问题.

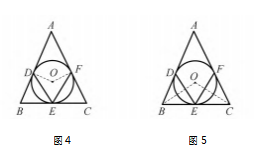
　　案例 3 在学习“直线与圆的位置关系”时，教 师可设置这样的问题 : 如图 4.ΔABC 的内切圆⊙O 分别切边 AB，BC，AC 于点 D，E，F，且∠A = 50 ° , 求 ∠DEF 的度数.

　　教师要求学生以小组合作的方式用两种解法解 答这道题.小组长组织学生先用一种方法解题，如果 会用第一种方法求解，再去思考另一种方法.小组长 提醒学生，如果不会用另一种方法求解，也不要紧张， 可将所有同学的解法集中起来，看有没有不同的解法; 如果有不同的解法，再彼此交流.

　　如图 4.连接 OD，OF，因为 ⊙O 切 AB 于 D，切 AC 于 F，所 以 OD ⊥AB，OF ⊥AC，∠A + ∠DOF = 180 ° . 又因为∠A = 50 ° , 所以 ∠DOF = 130 ° . 根据圆 周角与圆心角的关系，易得∠DEF = 65 ° .

　　对于第二种解法，大多数组员没有思路，小组长 就让个别有思路的学生提供解法.一个组员提供了 这样的思路，即利用切线长定理和内心性质来求解. 依照这样的思路，大多数组员给出了本题的另一种 解法.

　　如图 5.连接 OB，OC，因为⊙O 是ΔABC 的内切 圆，所以 OB 平分∠ABC，BD = BE，OB ⊥DE，∠OBC= 1/2∠ABC.同理易得 OC⊥EF，∠OCB =1/2∠ACB.

　　根据四边形的内角和，易得 ∠BOC + ∠DEF = 180 ° . 又∠BOC = 180 ° - ( ∠OBC + ∠OCB) ，根据三角形内角和定理，易得∠BOC = 90 ° +1/2∠A= 115 ° ,从而可得∠DEF = 65 ° .

　　由此可以看出，当教师建构出合作支架，学生就 能更全面展示自己的能力，每个人都能展示才能，每 个人又能依托别人获得成长.因此教学中教师要多 给学生合作的机会，让学生获得更多的自信，也获得 更多的成长.

　　4 建构互动支架，引导学生交流思维

　　提升课堂教学的质量是落 实“双减”政策最 有效的方式之一.要提升教学质量就要让学生的 思维活跃起来，就要给他们更多互动的机会.教 师可让学生与问题互动，让学生以自己的方式理 解问题 ; 也可让学生与教师互动，向教师提 出 问 题，激活学生的创造性思维 ; 还可让学生之间互 动，交换各自的问题与各自的成功之处.因为互 动，课堂成为思维的狂欢地，学生就能获得多元 化的生长.

　　案例 4 如图 6.在矩形 ABCD 中，AD = 6.AE⊥ BD，垂足为 E，ED = 3BE，点 P，Q 分别在 BD，AD 上， 则 AP + PQ 的最小值为多少?

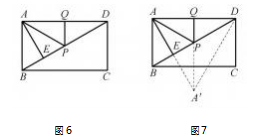
　　为解决本题，学生首先与问题互动，即学生与问 题对话，学生依据数学学习经验作出如下的思考 : 本 题属于线段和最短问题，可以把几条线段连接成一条线段，再利用“两点之间线段最短”求解.也就是 说学生想将本题的结论转化为“两点之间线段最 短”问题.学生易发现本题的本质就是要找到相关 点关于直线的对称点，进而实现“折”转“直”.学生 再次与问题对话，学生发现需作 A 点关于 BD 的对 称点 A'，连接 A'D，PA'，如图 7 所示. 当 A'，P，Q 三 点在一条线上时，A'P + PQ 最小.再次与问题互动， 学生发现依据“垂线段最短 ” ，可知当 PQ ⊥AD 时， A'P + PQ 最小.有了这样的与题目的互动，学生可 设 BE = x，则 DE = 3x.因为四边形 ABCD 为矩形，且 AE⊥BD，所 以 ΔABE ∽ ΔDAE，AE2 = BE · DE，即AE2 = 3x2 ，AE = ■ 3 x.在 RtΔADE 中，由勾股定理，易得出 AD2 = AE2 + DE2 ，即 62 = ( ■ 3 x) 2 + (3x) 2 ，解得 x = ■ 3 ，所以 AE = 3.DE = 3 ■ 3.学生发现问题已经转 化为AP + PQ = A'P + PQ = A'Q.如何求 A'Q 的长， 学生与教师互动起来.教师提醒学生可将 A' Q 转 化为另外一条线段的长，对 照 图形，学生发现可 能是 DE 的长.只 需证 明 ΔAA'D 是等边三角形， 就能证明 A'Q = DE.学生 由 A'A = 2AE = 6 ，AD = A'D = 6 ，得出ΔAA'D 是等边三角形.由此可 以看 出，学生在与问题、教师 的互动 中，不但提升 了解 题能力，也提升了学习的效率.

　　对教师而言，建构多元的支架就意味着进一步 挖掘学生的潜力.因此教师要依据不同的问题、不同 的学生、不同的认知，建构多元化的支架，让学生不 断地思考，发现更好的自己.建构支架的最终目的是 为了不建构支架，因此教师在建构支架的同时，要给 学生自主的机会，让他们自己学着不依靠教师的提 醒，就能单独地解决问题.

参考文献 :

　　[1] 肖月季.“支架式”教学模式在初中数学教学中 的应用: 以“一次函数”概念教学为例[J].数学 教学通讯，2019(17) : 21-22 .

　　[2]朱飞燕.支架式教学在初中数学教学中的应用 策略探 究: 以二次 函数教 学为例[J].考试周 刊，2021(86) : 82-84 .