摘要:文章在圆锥曲线第三定义的基础上，总结了圆锥曲线的若干二级结论，并举例分析其应用.

　　关键词:圆锥曲线第三定义;中点弦;应用

　　圆锥曲线的第三定义平面内，我们把与两个定点的斜率之积等于定值(非零常数)的点的轨迹叫做圆锥曲线(椭圆、双曲线、圆).

　　说明:这个定义中的三个曲线不完整(缺两个点).

　　具体可表述为下列三种情况:

　　设A(－a，0)，B(a，0)(a＞0)，动点P(x，y)，如果kPA×kPB=m(非零常数)，当m=－1时，点P的轨迹为圆(不含A，B);当m=(－1，0)时，点P的轨迹为椭圆(不含A，B);当m=(0，+∞)时，点P的轨迹为双曲线(不含A，B).

　　证明上述三种情况，如下:

　　对于(2)(3)中的方程，大家应该非常熟悉了，它们分别表示焦点在x轴上的椭圆与双曲线，而焦点在y轴上的椭圆与双曲线在后面我们再做说明.

　　根据上述研究，椭圆还有下列结论及推广:

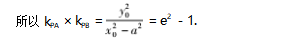
由于A，B两点关于原点对称，所以结论1可做如下推广:

　　通过类比，我们不难发现双曲线也有类似的性质，如下:

　　上面研究的这些圆锥曲线焦点都在x轴上，如果换成焦点在y轴上的圆锥曲线呢?上述结论和推广都会发生变化，具体变化为替换.

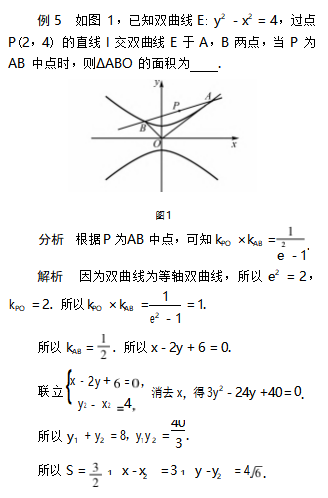
上述结论1，2及其推广1，2，3，4，对于我们提高解小题速度非常有帮助，同时，圆锥曲线中的二级结论很多，需要我们的学生在学习过程中多积累，还要善于总结.

　　参考文献:

　　［1］中华人民共和国教育部．普通高中数学课程标准(2017年版2020年修订)［M］．北京:人民教

　　育出版社，2020．