摘 要 : 文章以一道圆锥曲线题为例，深度挖掘“等腰直角”条件的转化，从多个角度进行探究，同时进行类比探究，加深对问题本质的理解，进而将方法迁移到高考试题和竞赛试题中，更具一般性.

　　关键词 : 圆锥曲线,等腰直角,探究,拓展

　　1 问题提出

　　解析几何是高中数学的重要内容之一，其本质 是以代数方法来研究几何特征，其特点是综合性强， 运算量大，变化较多，对学生的能力要求很高，而 圆锥曲线作为解析几何中的重中之重，在 问题考 查中，可能会出现一些特殊的条件，如何在代数 环境中处理呢? 本文以 2021 年江苏七市一模第 22 题中出现的“等腰直 角”条件为例，对此类 问题进行探究与拓展.

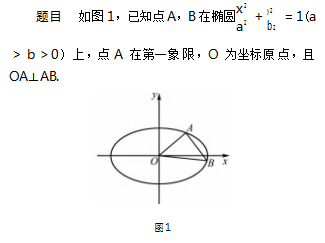
　　2 试题解法

　　点评 此方法选择的是点参，借助等腰直角三角形的条件用点 A 坐标来表示点 B 坐标，再根据点在椭圆上，构建关于 x1(y1) 的二次方程，从而由根的分布解出结果，体现了曲线与方程的联系.

　　解法 2 设直线 OA 的斜率为 k(k>0) ，倾斜角 为 θ(0 ° < θ <90 ° ) ，因为 ΔOAB 是等腰直角三角形 ( 点 O，A，B 按顺时针排列) ，且 OA⊥AB，则直线 AB 的斜率 kOB = tan( θ - 45 ° ) 或 kOB = tan( θ + 135 ° ) .

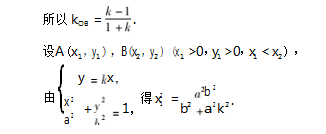
　　点评 此方法选择的是斜率作为参变量，借助 于角的中间量找到坐标关系，进而得出关于 k 的方 程，同样根据根的分布即可解决，充分体现了角和斜率在圆锥曲线中的运用.

　　点评 方法 3 主要是中间的处理方法与方法 2 有些区别，通过对两个等式的特殊处理，结合基本不 等式即可轻松求出，这里也充分体现了基本不等式在处理一些最值问题的优势.

　　点评 方法 4 选择了角参，借助于参数方程可 以把等腰直角三角形的条件进行转化，进而得到点 坐标的三角表示，把所求的比值用所设角的三角函 数来表示，从而借助于三角函数知识求得最值，当然 ①式的处理也可齐次化，化为关于 tanθ 的函数来解 决，充分体现了三角函数与圆锥曲线的联系.

　　点评 考虑到 图形 的特征，这里仅把椭圆的 背景推广到双曲线的右支上，根据前面的方法， 同样可以进行处理，也体现了圆锥曲线的一些家族特性.

　　4 真题链接

　　( 1) 求 C 的方程 ;

　　(2) 若点 P 在 C 上，点 Q 在直线 x = 6 上，且 | BP | = | BQ | ，BP⊥BQ，求ΔAPQ 的面积.

　　解析 不妨设 P，Q 在 x 轴上方，因为点 P 在 C 上，点 Q 在直线 x = 6 上，且 | BP | = | BQ | ，BP⊥BQ， 过点 P 作 x 轴垂线，垂足为点 M，设 x = 6 与 x 轴交 点为 N，根据题意画出图形.

　　由| BP | = | BQ | ，BP ⊥BQ，∠PMB = ∠QNB = 90 ° , 又 ∠PBM + ∠QBN = 90 ° , ∠BQN + ∠QBN = 90 ° , 则∠PBM = ∠BQN.根据三角形全等条件“AAS ” ，可得ΔPMB≌ΔBNQ.

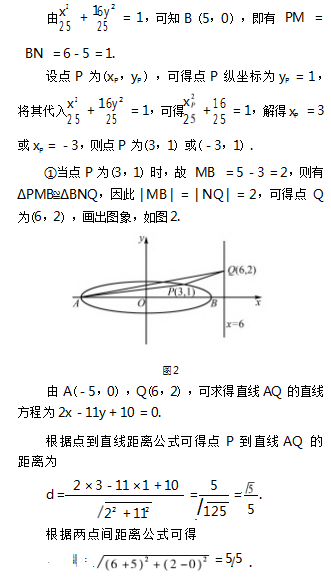
　　5 反思总结

　　在数学教学中，对于问题的解决，要能够放开思 维，不必拘泥于问题背景中的常规思路，就像本文开 头的问题，等腰直角三角形的条件可以从点、角、斜 率等多个方面来研究，这样才能真正体现数学知识 的全面性、融合性，也才能更好地促进学生能力的提高、思维的提升、素养的形成.

参考文献 :

　　[1] 中华人民共和国教育部.普通高中数学课程标 准(2017 年版) [M].北京: 人 民教育 出版社，2018 .