摘要:2022年新高考数学Ⅰ卷圆锥曲线大题重点考查学生的转化能力与计算能力，本文从解法赏析、探本溯源、解题思路与解题反思四方面进行探讨，对新高考后的学习提出几点建议.

　　关键词:圆锥曲线;解题思路;通性通法

　　1真题呈现，解法赏析

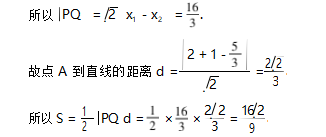
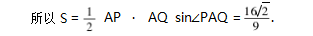
　　2探本溯源

　　其实本次新高考的圆锥曲线大题并不是横空出世，更像是经典重现，理由如下:

其实我们回归教材同样也是可以找到类似条件的例题，如人教A版数学选择性必修一第三章第一节例3“设A，B两点的坐标分别为(－5，0)，(5，0)，直线AM与BM相交于点M，且它们的斜率之积是-4/9，求点的轨迹方程”.

　　3理清思路，掌握通法

　　从三种解法当中我们可以总结出圆锥曲线大题的分析思路与答题思路，总的可以概括为如图1所示.

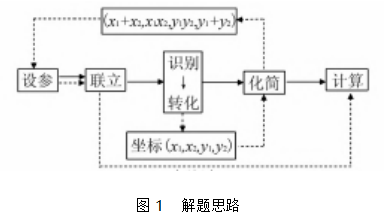
　　其中实线表示的是答题时的步骤，虚线代表的是分析思路，拿到圆锥曲线大题时我们应该从识别问题条件入手，将条件全部转化为坐标之间的关系，将几何问题代数化，化抽象为具体.

　　4解题反思，洞见未来

　　首先，淡化技巧，注重通法．不可否认，总结一些技巧在一定程度上可以帮助我们更有效解决问题，但是技巧的过度化使用是与核心素养的要求背道而驰的．以该题的解法3为例，齐次化也是一种盛行的技巧，对比法1法2的通性通法，不难发现，法1和法2是学生更容易理解与掌握的，也是更能够迁移到其他题目当中去的．所以我们应该淡化特殊技巧，注重对通性通法的深入理解和综合运用，学会将知识和方法内化为自身的知识结构.

　　其次，回归教材与真题，以考引教．我们既要用好教材也要用好真题，从教材中追本溯源，让教材成为“源头活水”，从真题中去寻找方向，让真题引导我们的教与学．在此基础上去变式、去探究、去反思、去创新，直至把握问题本质.

　　最后，洞见未来，有的放矢．从这次新高考中可以发现，题目更具情境性、开放性与创新性，它们紧紧围绕课程标准，并且以核心素养为中心，同时也发挥数学的育人功能，助力基础教育提质增效．可以预见，未来的新高考会更加注重对学生的理解能力、抽象能力、建模能力、计算能力、创新迁移能力的考查.

　　参考文献:

　　［1］唐永．回归教材:提升学生核心素养的有效途径［J］．数学通报，2020，59(07):40－43+48.