摘要:本文结合课例“体积和容积”的教学实践,在学生认知经验和理解图形概念本质的基础上,提出课堂教学要设计有根、有感、有品的学习路径,实现“教学做合一”,发展学生思维水平,促进学生核心素养的发展。

　　关键词:学习路径  空间观念  发展思维

　　《义务教育数学课程标准(2022年版)》倡导教学要基于儿童的立场,创设真实问题情境,设计引发学生思考的活动,引导学生触及概念本质,培养学生核心素养。北师大版《数学》五年级上册“体积和容积”一课是属于“图形与几何”部分的内容,下面结合教学实践,探析如何设计有根、有感、有品的学习路径,以及如何建构几何核心概念,最终促进思维发展和空间观念形成。

　　一、有根:把握学习起点,直击认知障碍

　　学情前测表明,五年级学生早就对体积有直觉的认识,并有相当程度的理解,但在学习体积概念时,仍存在两个障碍:一是用“空间”描述体积,似乎比体积本身更难理解;二是表面积(或占地面积)和质量会对体积含义的认识产生困扰。淡化“空间”概念的解释,排除“面积”“质量”的干扰,教学是不能回避的,需要层层剥茧直面应对。

　　1.观察比较,感知体积与面积的不同

　　首先,教师出示两张大小不一的白纸,让学生仔细观察比较:哪一张纸大?接着,教师再出示两个大小不一的红薯,继续让学生观察比较:哪个红薯大?待学生回答后,教师提出问题,引发学生思考:同样是比大小,这两个实验有区别吗?学生讨论交流汇报:两者有区别,一个是面积的大小,一个是体积的大小;一个是平面图形的面积,一个是立体图形的体积。教师顺势板书“体积”,让学生举例说出生活中还有哪些物体有体积。

　　然后,教师出示封面大小一样的两本书,让学生只看到正面,并观察哪本书的体积大?此时,学生出现两种判断结果:因为封面大小一样,所以体积相同;比较物体大小,不能看表面大小,还要看它的厚度。教师将两本书平放,让学生观察这两本书的厚度确实不一样,厚度大的体积就大。

　　2.称量比较,感知体积和质量的不同

　　教师拿出无法目测出大小的土豆和红薯,继续让学生观察比较两个物体的体积大小,并说出判断它们大小的办法。当学生说用称重的方法判定体积大小时,让学生称量其质量大小,引发学生思考、辩论。学生举例说明,同样重的铁和棉花,体积是不一样的,从而得出以下结论:不同的材料,不能用质量的大小比较出体积的大小。

　　3.思考

　　观察是培养空间观念的前提。通过观察和辨析“两张纸比较大小与两个红薯比较大小”实验的不同和学生观察封面大小一样而厚度不同的两本书的体积,让学生理解物体的体积的刻画要从三个维度(长、宽、高)去描述,从而实现二维平面到三维立体的有效过渡,有效地突破面积对体积认知的干扰。当学生提出用称量的办法去比较土豆和红薯的大小时,启发学生辩论、质疑、例证,达成统一认识:不同材料的物体,质量与体积没有直接关系。教师直击表面积和质量的干扰,对空间概念的淡化处理,都是根植于学生原有经验和认知需求进行情境创设的。这样的问题情境能够走进学生的“最近发展区”,让有意义的学习真正发生。

　　二、有感:巧设操作活动,引发数学思考

　　教师要设计有效的操作学习活动,引导学生在观察比较、合作交流、思辨质疑中,主动探析问题本质,建构核心概念。有效的操作学习活动,应该引发探究,注重过程体验,引导积极思考,进行思维创新,也就是要求学生在“说”数学中,进行质疑思辨理性分析,在“做”数学中,进行验证归纳,积累思维活动经验。

　　1.操作比较,揭示体积的概念

　　教师继续出示土豆和红薯,让学生讨论汇报比较它们体积大小的方法。

　　一是切割法。学生想到把它们分别切成最大的长方体后,再比较长方体的大小就可以了。有的同学提出疑问:切去的部分也是原来体积的一部分,这一部分是无法比较大小的,所以也不能断定原来体积的大小。

　　二是排水法。学生发现切割法仍无法比较土豆和红薯体积的大小时,继续寻求更优化和简洁的方法———排水法,就是将土豆和红薯放在装足够多水的容器里,看排开水的多少,排开的水多,体积就越大。此时,老师让这两位学生台前演示,其他学生认真观察和积极思考:水面为什么会上升?哪个水杯上升的水多?学生观察发现,红薯所在的杯子上升的水多,并给出合理解释:红薯所占的空间大,排开的水就多,所以红薯的体积大。

　　教师顺势引导学生归纳概括体积的定义:物体所占空间的大小,叫作物体的体积。

　　2.猜测验证,揭示容积的概念

　　首先,教师出示大小明显不同的一个双层玻璃杯和一个塑料杯,其中双层玻璃杯较大些。教师指出像这样空心的、能容纳物体的东西就叫容器。其次,教师让学生猜测哪一个杯子盛的水多,很多学生认为体积较大的双层玻璃杯盛的水较多。再次,教师让一名学生演示,将塑料杯中满满的一杯水往玻璃杯中慢慢地倒,结果发现,装满玻璃杯后,塑料杯中还剩一些水。

　　这一实验说明:玻璃杯盛的水少,塑料杯盛的水多,体积大的物体不能表示容纳的东西就多。这时,教师揭示容积的概念,并板书:容器所能容纳物体的体积,叫作容积。

　　要求学生试着用“容积”这一概念解释双层玻璃杯盛水较少的原因,虽然双层玻璃杯的体积较大,但它的容积较小,所以盛的水少。学生在讨论交流中,初步感知体积和容积的不同。

　　3.思考

　　陶行知先生倡导“六大解放”(解放学生的脑、双手、口、眼、时间和空间)的教学理念,要求把学习的基本自由还给学生。动手操作、观察思考又是培养空间观念的基础。操作活动的精心设计,能够引发学生主动探究的欲望。学生在层层设疑中,在激辩问难中,在动手操作中,在深度对话中,逐渐形成正确的“空间”概念,从而加深对体积和容积这一核心概念的本质把握———容积,就是容器所能容纳物体的体积。本环节设计匠心独具,学生通过操作进行思考或通过思考进行操作,亲自参与,现场感受,实现由“动手操作”转向“积极思考”,在实效学习活动中有所悟、有所得、有所感。

　　三、有品:感悟思想方法,发展高阶思维

　　有品的数学教学应该是有内涵的教学,应该关注数学学科独有的思想与方法,发展学生高阶思维,培养学生理性分析精神。体积和容积这两个概念比较抽象,有很多相似之处,容易混淆。教师应让学生在充分感知、多样体验的基础上,归纳概括出两者的区别和联系,在深刻剖析中,感悟思想,形成智慧。

　　1.动态演示,沟通体积和容积的联系

　　教师课件出示一个长方体的纸箱,提问:如果让这个纸箱体积不变,容积变小,你该怎么办?学生先进行空间想象,让纸箱里面塞些东西,它的空间变小,所装的东西就会变少,容积就变小。教师利用动画演示纸箱被逐渐填充、填满的过程。继续追问:同样这个纸箱,如果让它容积不变,体积变大,你该怎么办?小组讨论交流:把纸箱的外壁给它加厚就行了。教师用课件动画演示纸箱外围被逐层加厚、体积逐渐变大的过程。学生能够直观地感知到唯一不变的是纸箱的容积。

　　通过两次动画演示,学生进一步理解体积和容积的区别和联系:一个物体的体积和容积是有联系的;一个物体一定有体积,但不一定有容积;如果物体有容积,它的体积是大于它的容积的,因为容积是在物体内部的。

　　2.拓展运用,加深对概念本质的理解

　　教师出示下面两个问题:

　　(1)数一数,想一想,图1中的长方体盒子能装多少个这样的小正方体?

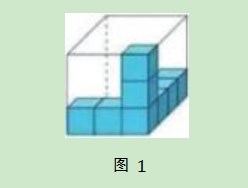
　　(2)图2中,谁搭的长方体体积大?

　　学生独立做这两道题,汇报不同的计算方法和比较方法。

　　计数法———数一数一共有多少个单位小正方体块,它们的体积就是多少;层加法———先算每一层有多少个小正方体块,再数一数有几层,每层的块数加起来,就是长方体的体积;连乘法———用长×宽×高,求出体积。

　　针对练习1的第三种方法,学生给出算理解释:用3×4×3最简单、快捷,因为3×4表示下面一层的块数,一共3层,所以再乘3,就求出装的总块数。追问:要想使长方体盒子的容积等于它的体积,该怎么办?学生对质思辨并想象出:当盒子厚度变薄,薄到变成零时,盒子的容积就是它的体积了。

　　针对练习2,学生先估一估,再计算体积的大小,并汇报比较的方法,加深理解体积概念的本质,同时渗透量感意识。

　　3.思考

　　想象是培养空间观念的关键。通过两次在“头脑”中对纸箱进行想象“改造”,在变与不变中,融通和理解体积和容积的关系,两者是针对同一物体而言,体积是从物体外部测量,容积要从其内部测量。如果说用“观察法”和“排水法”比较体积,重在“目测和量”,更多体现的是物理上的方法,那么,数学方法应该去“计算”物体的体积———计算物体所能细分单位体积的个数,真正使学生触及体积的本质———单位体积累加的结果。设计练习环节,一则让学生在想象中,让容积破“壁”而出———当壁厚渐变为零时,此时容积即等于体积,极限思想应运而生;一则让学生在推理计算中,掌握计算方法的多样化和优化策略。这一环节的设计,既实现估测到精准计算的“量化”跨越,又体现方法和思想的深度融合。

　　四、结语

　　本节课从基于学情前测读懂学生、基于问题解决设计操作活动、基于数学本质提炼思想方法三个角度设计有根、有感、有品的学习路径,引导学生在直观感知、操作思辨、推理计算中,把握“体积和容积”这两个核心概念的本质及区别,有效达成学习目标。在问题引领和任务驱动下,学生经历抽象概念可视化体验,丰富学习画面感,又在反思批判中,习得问题解决方法,感悟其中蕴含的数学思想,助力发展空间观念和提升思维品质。

　　[1]陶行知.陶行知教育名篇[M].北京:教育科学出版社,2021:62.

　　[2]张奠宙.深入浅出,平易近人———怎样测量长度、面积和体积?[J].小学教学(数学版),2014(9):6-8.