摘要：文章首先阐述了高职院校高等数学课程思政教学现状，然后提出了高职院校高等数学课程思政教 学的优化路径，最后论述了高职院校高等数学课程思政教学的具体实施。

　　关键词：课程思政,高等数学课程,高职院校

　　党的十八大以来，习近平总书记高度重视文化自信，强调“文化自信，是更基础、更广泛、更深厚的 自 信”[1] 。文化自信是一个国家、一个民族、一个政党对 自身文化价值的充分肯定和对自身文化生命力的坚定信念 。而高等数学作为高职院校的公共基础课，也 肩负着思想政治教育的神圣使命 。基于此，如何将中华优秀传统文化融入高等数学课程，便成为高职院校 数学教师的新任务。

　　数学文化教育将数学思想、数学方法与各学科、 各文化领域的应用相融合，有助于引导学生树立正确的历史观、民族观、国家观，同时引导学生树立坚定的文化自信，以达到以文化人、以文育人的教育目标。而在高职院校，高等数学课程内容不仅包含古今中外数学思想、数学方法与各种文化的相融，还能引导学生树立正确的人生观、价值观、历史观、民族观、文化观， 强化学生的社会责任意识和规则意识 。因此，高等数学课程不仅是传授数学知识和技能的一门基础课，同时也是高职院校实施文化素质教育，落实立德树人这 一根本任务的重要载体。

　　一、高职院校高等数学课程思政教学现状

　　(一)对高等数学课程思政理解不深

　　对于高职院校来说，在传统的高等数学课程教学 中，教师更注重学生对定义的理解、定理的掌握、性质 的应用和计算能力的提升，忽视了对学生思想政治素质的培养 。部分教师认为高等数学内容过于抽象，不 适合进行课程思政教学，对“在课程中真切践行课程 思政”的认同不够强烈，尚未形成课程思政建设的思 想共识和实践自觉。

　　(二)对高等数学课程学情分析不足

　　目前， 高职学生基本上都是’00 后， 具有崇尚自 我、追求个性的特点，也具有思维活跃、创新的特点，但与此同时，’00 后学生也是一个缺乏独立性锻炼、自 我评估能力不足的群体。特别是“3+2”的学生(即中职 三年+高职两年) 数学基础比较薄弱，对数学学习兴趣 不足，数值计算和证明的能力欠缺 。教师在教学过程 和课程思政建设的过程中， 往往忽视了学生主体，只 是简单机械地重复和硬性“灌输”，导致与学生的交流 互动不足，没有真正体现出高等数学蕴含的“探索真 知、求真务实”的精神。

　　(三)对高等数学课程教学模式应用不当

　　目前， 高职院校数学教师在讲授高等数学课程 时，往往通过“定义、性质、定理、计算”四个步骤来实 施，具有很强的逻辑性和理论性 。然而高职院校的学 生数学基础薄弱，逻辑能力不足，对高等数学课程内 容理解不深，对高等数学课程的兴趣不足，很难较 好地理解高等数学课程内容 、掌握数学计算方法 。 教师在教学过程中， 虽然也在不断细化各章节 、各 知识点的内容设计和思政元素的融入， 但忽视了效 果评估环节，只是简单地停留在教师讲思政、学生听 故事的层面，并没有将中华优秀传统文化“润物细无 声”般地融入课堂，这使得课程思政建设和效果缺乏 评估依据和标准。

　　(四)高等数学课程标准不一致，制度保障不完善

　　目前，高职院校高等数学课程尚未与本科高等数 学课程一样，制定一套完整且统一 的课程标准 。不同 职业院校往往根据不同的学生需求和专业课需求制 定课程标准， 且教师更注重将数学知识融入专业课 程， 而忽视了高等数学课程的思想政治教育功能，即 以“实用为主，够用为度，为专业服务”为原则制定职 业院校高等数学课程标准 。 同时，职业院校的地区差 异、学生基础差异较大，因此建设能够体现职业岗位 需求、促进学生职业能力发展、培养学生思想政治素质的课程标准难度较大 。当下，在走访省内诸多高校 之后，笔者发现高等数学课程已经逐渐边缘化，许多 专业课程并不需要学生掌握相应的数学知识的推导、 证明、计算，这导致数学教师的教学科研活动不能顺 利展开 。 同时，在教学平台、教学团队建设上，数学课 程组缺少与学校职能部门如教务处、学生处、团委等 的沟通，且未形成常态化发展机制。

　　二、高职院校高等数学课程思政教学的优化路径

　　(一)培养教师的价值认同感

　　高职院校要提升高等数学教师的主体意识，使 其发挥示范引领作用 。具体而言，高职院校要充分发 挥教师在课程思政过程中的主导地位， 强化教师课 程思政的理念， 使教师在教学过程及与学生交流过 程中，结合学生特点，转变教学方式，逐步实现思想 政治教育全覆盖，从而培养“探索真知、求真务实”的 时代青年。

　　(二)推进思政元素与高等数学的有机融合

　　教师在制定课程标准时， 要明确高等数学课程 思政教学目标，并巧妙地将思政元素融入教学过程， 使学生不仅具备运算能力 、逻辑能力 、空间想象能 力，还能树立正确的世界观、人生观、价值观 。对于基 础薄弱的学生， 教师可适当减少教学过程中数值计 算和数学证明的内容，同时注重学生数学文化、数学 史、数学美的教育，将古今数学史、数学思想贯穿高 等数学教学过程， 这样既有利于培养学生的数学文 化素养， 又能充分激发学生学习高等数学课程的热 情 。 因此，课程组要积极组织教研活动，通过集体备 课的形式，充分挖掘思政元素，为高等数学课程思政 的开展提供基本保证。

　　(三)优化高等数学课程思政教学模式

　　对于高职院校来说， 在高等数学日常教学中， 教师可以适当地调整教学模式，充分利用多媒体资 源转变学生对传统数学教学的印象 。 教师在教学 中，可通过恰当的教学环节，灵活巧妙地融入思政 元素，如讲解部分数学定义时，通过引入中国古代 数学家的故事，激发学生的爱国情怀;讲解数学发 展史时，通过引入历史人物历史故事，增强学生的 文化自信;结合线上线下教学模式，充分发挥信息 化教学的优势，利用信息化教学平台、教学视频、辅 助软 件 (MATLAB、SPSS、Mathmetics、Excel) 等，激 发 学生学习高等数学的热情，使学生掌握更多更加实 用的数学能力和数学知识。

　　(四)构建特色课程标准体系，推进思政元素的 融入

　　对于高职院校来说， 目标就是将学生培养成掌 握一定技术的技能人才，为实现这一目标，其要以教 育目标为前提、以提升质量为核心、以满足需要为目 标、以彰显特点为重点，构建具有科学性 、前瞻性与 示范性的高职特色课程标准体系， 并研究配套的高 等数学课程评估标准，以便优化课程体系，从而更好 地衡量中华优秀传统文化在高等数学课程中起到的 作用，有效推进思政元素的融入 。 同时，课程组要积 极与学校职能部门沟通交流，联合教务处、学生处、 团委等建立线上线下全覆盖的教学平台， 并开展多 方位 、多维度 、多领域的高等数学课程思政建设活 动，实现课程教学内容“理论实践一体化”，从而强化 学生思想政治教育 。此外，学校要建立并完善高等数 学课程“诊改”机制，切合实际开展教学督导、教学评 价、学生评教、教师互看互学互鉴等活动，以进一 步 保障中华优秀传统文化在高等数学课程内容的融 入，推动高等数学课程思政的实施，确保高职特色课 程标准体系的构建[2]。

　　三、高职院校高等数学课程思政教学的具体实施

　　导数作为高职院校高等数学第二章节的重要定 义，是高等数学课程中的重要概念之一，同时它也在 这门课中起到了承上启下的作用，是连接初等数学和 高等数学之间的桥梁 。 因此，笔者现以高等数学课程 中的导数为例，阐述课程思政教学的具体实施。

　　(一)导数概念的引入(物理意义、几何意义)

　　一方面，高等数学课程教师可以通过讲解“中国速度”引入导数的概念。例如，教师可通过讲述如何计 算我国运动员在东京奥运会田径男子百米半决赛中 取得 9.83s 成绩时的瞬时速度和瞬时加速度及如何计 算中国高铁“复兴号”在运行过程中的瞬时速度和瞬 时加速度，引申出导数的物理意义。另一方面，高等数学课程教师可通过讲述古代千里望的构造，即如何设 计凹透镜、凸透镜的曲面弧度，从而增大视角，提高分 辨能力，引申出导数的几何意义[3-4]。

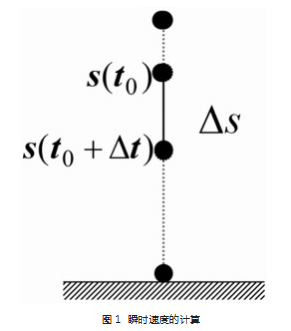
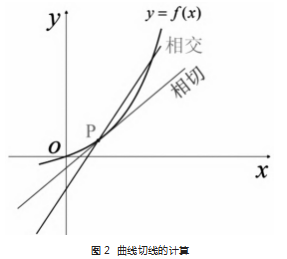
　　针对瞬时速度的计算，教师可先引导学生回顾中学时学过的自由落体运动内容，让学生思考自由落体 运动速度方程和加速度方程是如何推导的(即理想状 况下的匀变速运动) [5]，如图 1 所示 。同时，教师可提示 学生利用极限的思想，即利用运动物体较短时间间隔 内的平均速度近似代替某一时刻的瞬时速度(极限的思想) 。当时间间隔充分小(Δt→ 0) 时，平均速度=瞬时速度，即 v(t) =v(t0) 。针对曲线一点处切线方程的计算，教师可先引导学生回顾中学时学过的直线方程的求解，然后再让学生思考曲线一点处切线方程的求解。之后教师可提示学生利用极限的思想， 即先计算曲线的割线方程，当 两个割点充分接近时近似代替曲线一点处的切线方 程(极限的思想) [6]，如图2 所示。当两个割点的横坐标 充分接近(Δx→ 0) 时，割线方程的斜率=切线方程斜率 (k'=k) 。文化自信的融入过程如下。教师可通过分享中华民族的故事， 培养学生高度的文化自觉与文化自信， 使其全面理解我国传统文化，树立民族自信心[7-8] 。 同时， 教师要提醒学生正视我国目前面临的机遇与挑战，坚定信念，振奋精神，奋发学习，报效祖国，从而努 力实现自己的伟大抱负。

　　(二)导数定义的引入

　　高等数学课程教师可以 自由落体运动物体的瞬 时速度计算为例，利用较短间隔时间内的平均速度近 似代替变速运动物体某一时刻的瞬时速度，让学生得出瞬时速度计算公式：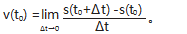

　　教师可以曲线一点处的切线方程为例，利用曲线 割线的极限形式得出曲线一点处的切线方程，让学生得出计算公式: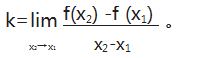

　　学生通过比较两个计算公式，可总结出导数的定义， 即当函数自变量改变量为 Δx， 因变量改变量为 Δy， 当 Δx→0 时，Δy 与 Δx 的比值趋向于一个固定常数：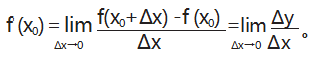

　　文化自信的融入过程如下 。教师通过总结规律， 可得出有效结论，告诫学生在平时学习中注重积累材
料，分析研究，归纳总结，透过现象看本质[9]。

　　(三)导数定义的提高

　　基础题型 1：基本初等函数求导。

　　高等数学课程教师可给出以下几个不同的基本 初等函数。

　　f1 (x) =x2

　　f2 (x) =lnx

　　f3 (x) =sinx

　　接着让学生利用导数定义求解基本初等函数的 导数 。 即先写出各个基本初等函数的自变量改变量 Δx 和因变量改变量 Δy。

　　Δ 1y= (x+Δx) 2-x2

　　Δ2y=ln(x+Δx) -lnx

　　Δ3y=sin(x+Δx) -sinx

　　然后利用导数的定义即可计算出各个基本初等 函数的导函数。

　　f1' (x) =2x

　　f2' (x) = 1/x

　　f3' (x) =cosx

　　基础题型 2：单侧导数。

　　高等数学课程教师可给出以下函数。

　　f (x) =|x|

　　接着让学生利用单侧导数的定义求解函数在x=0 处的导数。

　　根据定理， 学生可得出函数在 x=0 处导数不存 在的结论。

　　文化自信融入过程如下 。通过教师演示、学生推 导这个过程，学生能体会到孟子所说的“故事半古之 人，功必倍之，惟此时为然”，即学习事半功倍的效果， 鼓励学生在今后的学习中， 要从以往的学习经验出 发，结合自身和他人的优点，不断努力提高自己[10]。

　　基础题型 3：讨论连续性与可导性的关系。

　　通过第一章节连续性的学习和本节课导数定义 的学习，高等数学课程教师可让学生思考函数在一点 处连续与可导的关系。通过连续的定义和教师给出的 例题，学生可总结出可导与连续的关系：可导一定连 续，连续不一定可导。

　　文化自信融入过程如下 。学生通过定义推导、例 题演练，可总结出连续与可导的关系，这好比“滴水可 以穿石，愚公可以移山，铁杵可以磨成针”的过程[11]。基 于此，教师可鼓励学生要勤奋刻苦、不怕困难、勇攀高 峰[12]，如此才能让学生在今后的学习中养成良好的学 习习惯，最终提高自己的学习成绩。

　　备考题型：教师讲解历年专升本 、微积分竞赛 习题。

　　文化自信的体现：精益求精，更上一层楼。

　　据上所述，高等数学课程教师借助中华优秀传统 文化引入数学知识，将思政元素融入课程学习，有助 于学生掌握学习内容，理解导数的定义，领会极限的 思想在导数中的运用，掌握导数的物理意义和几何意 义， 熟练运用导数的定义求解基本初等函数的导函 数、变速运动物体的瞬时速度和曲线在一点处的切线 方程法线方程，使学生将枯燥乏味的数学知识与现实 生活和历史故事结合起来，充分培养学生的创新精神 和独立思考的能力，进而有助于更好地完成教学目标 和教学任务[13] 。教师要不断挖掘高等数学学科内在的 哲理和价值，将教学目标和德育目标相结合，设计具 有启发性的问题，以问题引导学生领会知识点蕴含的 思政素材 。概言之，教师要坚持“知识传授与价值引 领”相结合的原则，将课程思政的教学目标明确于教 学大纲，固化于课程教案[14]。

　　四、结语

　　高等数学这门课程与其他课程不同的地方就在 于它本身有着丰富的文化内涵， 将其与思政教育融 合，既符合全面深化高校思想政治教育改革的本质要 求，又能增强思想政治教育在专业课程教学中的指导 力量，进而增强大学生的文化自信及对中华优秀传统 文化的价值认同，从而为高校课程思政建设提供参考 和借鉴[15-16] 。然而当前高职院校高等数学课程思政教 学虽然取得了一定的成效， 但仍有许多问题亟待解 决 。对此，教师应该认识到在高职院校高等数学课程 教学中开展思政教学的价值和意义，然后根据数学学 科的特点，将思政教育融入数学教学各个环节，将思 政教育贯穿学生数学学习的全过程，这样才能提升高 等数学课程思政教学的成效，进而培养全面发展的社 会主义建设者和接班人。

参考文献：

　　[1] 习近平:在庆祝中国共产党成立 95 周年大会上的讲话[EB/OL]. (2016-07-01)[2022-12-02].http://www.gov.cn/xinwen/2021-04/15/content_ 5599747.htm?ivk_sa=1023197a.

　　[2] 教育部办公厅关于开展课程思政示范项目建设工作的通知[EB/ OL].(2021-03-11)[2022-12-02].http://www.moe.gov.cn/srcsite/A08/s7056/ 202103/t20210322_521681.html.

　　[3] 郭书春. 中国传统数学史话[M].北京:中国国际广播出版社,2012. [4] 徐传胜,周厚春.数学史讲义概要[M].北京:电子工业出版社,2010. [5] 刑治业.从案例教学视角探讨课程思政与高等数学的融合策略[J]. 科教文汇,2020(2):71-72.

　　[6] 于水源,鲍勇,徐美林.高等数学中数列极限的教学研究[J].学科 探索,2020(39):39-41.

　　[7] 邱仰聪.基于数学史教育的高校数学文化育人功能研究[J].顺德 职业技术学院学报,2019(17):36-40.

　　[8] 李蕾.高职院校数学文化教育:内蕴、价值与路径[J].教育与职业, 2015(16):91-94.

　　[9] 曹丹平, 印兴耀.加拿大 BOPPPS 教学模式及其对高等教育改革 的启示[J].实验室研究与探索,2016.35(2):76-78.

　　[10] 左励明.文化自信视域下高校思政课程实践教学保障体系建设 研究[J].吉林省教育学院学报,2021(37):84-87.

　　[11] 张驰 .教师的课程思政建设意识及其培育[J]. 思想理论教育 , 2020(9):71-76.

　　[12] 魏巍,余亚辉.金课背景下融入思政元素的高等数学教学设计 的探索:以“定积分的概念”为例[J]. 国际教育,2021(12):112- 113. [13] 罗珊.浅谈弘扬中华优秀传统文化坚定大学生文化自信[J].豫 章师范学院学报,2021(12):16-22.

　　[14] 张迪.基于文化自信的中医护理学课程思政教学改革与实践[J]. 循证护理,2021(18):2505-2508.

　　[15] 李晨.高职高专院校学生文化自信培养的教学策略研究:以《茶 文化和茶艺》课程为例[J].福建茶叶,2020(10):118- 119.

　　[16] 邱仰聪.宋代以后中国古代数学发展盛衰的原因分析[J].湖北 函授大学学报,2014.27(1):104- 106.

　　其他作者简介：张茜(1987— )，女，讲师，硕士 。研究方向：双曲型 偏微分方程。