摘要:文章主要从把字母看作变量或把代数式看作函数、利用函数的性质、根据结构构造函数比较大小和数形结合四个方面介绍了函数思想在比较大小问题中的应用．

　　关键词:函数思想;数形结合;同构

　　函数思想是用运动和变化的观点，分析和研究数学中的数量关系，建立函数关系或构造函数，运用函数的图象和性质去分析问题、转化问题，从而使问题获得解决．利用函数思想解题指的是一种意识，一种解题时的思维习惯，具体说就是用变量和函数的观点来思考问题．对于比较大小问题，我们利用函数思想去思考，往往可以起到简化的作用．

　　1把字母看作变量或把代数式看作函数

　　点评例1虽然用不等式的性质也很容易证明，但是利用函数的思想求解则是从另外一个角度看问题，这在例2中其优点就很明显，例2若是用不等式的知识求解就比较困难．

　　2利用函数的性质比较大小

　　点评本题构造函数的方法称为同构法，同构法是目前高考比较热门的比较大小的方法．数学中的同构式是指除了变量不同，而结构相同的两个表达式．许多比较大小的问题，通过等价变形，可以转化为同构式，然后构造函数，利用函数的单调性求解．

　　点评本题中a，b，c非常接近，又涉及到对数和根式的运算，直接很难比较，三个数中的1．01，1．02，1．04非常接近，因此引入x=0．01构造函数来比较大小，比较巧妙!

　　4数形结合

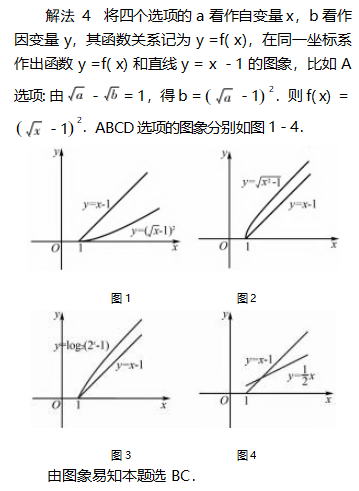
　　点评本题四种解法，解法1仅仅是作为选择题的解题策略，其对于BC的正确性并没有真正证明;解法2的解法极大地依赖代数变形，不同的选项其变形方式不一样;解法3和解法4则是从函数这个统一的角度去思考问题，解法3借助函数增长速度(二阶导函数的符号)，解法4从数形结合的角度思考．

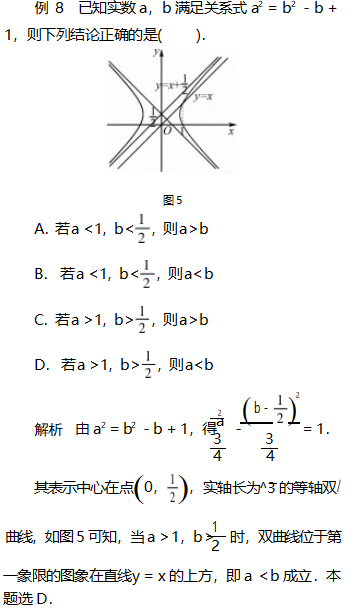
　　点评本题实数a，b满足关系式a2=b2－b+1虽然不是函数关系式，但是借助函数的思想(变化的观点)利用数形结合就很容易得到答案D，若是用不等式的知识则很难得出正确的答案．

　　参考文献:

　　[1]闫伟．例说指数与对数比较大小问题的求解策略[J]．高中数理化，2020(Z2):30－32．