摘要:本文以几道高考试题和模拟题为例，探究了高考题和模拟题中一类圆锥曲线中直线过定点问题“不联立”的解决办法，同时对圆锥曲线相关性质的教学给出了一点建议．

　　关键词:圆锥曲线;联立;定点;斜率

　　圆锥曲线定点问题一直是高考的重点热点问题，对于这类问题需要考生掌握扎实的基础知识和基本的解题方法．直线过定点问题常见的解题方法主要有两种:一种是通过引进参数表示出直线经过的两个点坐标，再由这两点确定直线的方程，从而经过化简得到直线的定点;另一种是直接假设出直线的方程，然后和圆锥曲线联立，再利用丰达定理找出直线中参数的关系，从而得到直线的定点．这两种方法一般都有联立所设直线和圆锥曲线方程，计算量很大，不易找到定点．本文专注于“不联立”的思路来找直线过的定点，所给的解决方案具有普遍性:

　　1“不联立”与椭圆

　　以下对第(2)问进行探究:

　　直线过定点(x0，y0)的问题，常通过假设直线的截距式y=kx+b方程，进而找到方程系数之间的关系来求得定点，这种解法是一种常用的方法，也是高考参考答案给出的方法．但许多考生并不能准确找到系数之间的关系，而且有的问题并不能用这种方法．这个时候我们可以尝试采用另一种思路:
　　假设点M(x1，y1)，N(x2，y2)，当直线AM，AN的斜率存在且不为0时，设直线AM的方程为y=k(x－2)+1．

　　与第一种思路相比，这种假设直线的方法相对更自然，但最后一步要准确找到直线的定点却并不容易，我们来看“不联立”的解决办法:

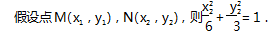
　　2“不联立”与双曲线

　　对于第(2)问，常规思路是通过假设直线AB，CD的方程，分别和双曲线联立可得M，N的坐标，从而用点斜式的方式得到定点，这个时候还要考虑直线AB，CD和坐标轴平行的情况．我们来看“不联立”的解决办法:

　　3“不联立”与抛物线

　　需要指出的是，例1中的点A(2，1)在椭圆上，所以是利用椭圆方程转化斜率之间的关系．而例2和例3中的点虽然不在椭圆上，但都是中点，故而可以用点差法的思路迅速得到斜率之间的转化关系．

　　圆锥曲线中的定点问题在高考中有广泛的应用，像这样以小专题的形式介绍圆锥曲线中存在的问题，短、平、快地一次性彻底地解决与其有关的问题，对学生解题水平的训练、思维能力的培养和学科

　　素养的提升，想来都是极好的．

　　参考文献:

　　[1]魏东升．衣带渐宽终不悔为“e”消得人憔悴———以“e2－1”为定值的有心二次曲线问题探究[J]．中学数学杂志，2021(09):29－31．