摘要：《义务教育数学课程标准(2022年版)》对“综合与实践”领域进行了全新的设计与编写，将其细分成“主题式学习”和“项目式学习”两部分。“模型意识”作为“模型思想”在小学阶段的表现，是主题式学习“用数学的语言表达现实世界”的呈现方式。文章以主题式学习为研究点，从结构化、活动化、问题化、反思化四个方面，从进阶、体验、应用、内化中探索小学数学模型意识培养的策略，以期发展学生的核心素养。

　　关键词：小学数学；主题式学习；模型意识

　　《义务教育课程方案(2022年版)》提出不少于10%的课时设计跨学科主题学习，而《义务教育数学课程标准(2022年版)》(以下简称《课程标准》)对“综合与实践”领域进行了全新的设计与编写，将其细分成了“主题式学习”和“项目式学习”两部分，旨在发展学生的模型意识和创新意识，进一步提高解决问题的能力，发展学生核心素养。“模型意识”作为“模型思想”在小学阶段的表现，是主题式学习“用数学的语言表达现实世界”的呈现方式。如何在“主题式学习”中进行“模型意识”的培养，笔者进行了以下尝试。一、主题学习结构化，在进阶中发展模型意识

　　(一)学段衔接进阶联系点

　　《课程标准》根据学生数学学习的心理特征和认知规律进行了学段的划分，学习目标逐段递进，强调教学内容的结构化及与核心素养的关联。笔者根据主题活动的类型、内容、模型的类别等分类方式，对主题活动进行分组，将其作为一个整体，通过学段衔接建立模型，培养学生的模型意识1。

　　如对主题活动的内容进行分类，统整三个学段中的“方位主题”,包含第一学段“我的教室”、第二学段“寻找‘宝藏'”、第三学段“校园平面图”。对这三个主题的模型意识培养目标进行细化，从“能用上下左右前后、东西南北描述物体的位置，在辨别和应用中体会方位的相对性”,到“能用东北、西北、东南、西南、‘几点钟方向’描述物体的位置及关系”,再到“通过具体的实地测量、构建比例尺、依据比例尺进行绘图等多个阶段，能使用数学语言描述出校园形状、校园内建筑等的位置及关系，并进行相互评价",抓准模型意识培养的要求，分层设置目标，体现了学段的衔接。教师在教学时，针对三个主题活动，从情境创设、学习方法、模型呈现等方面进行衔接，体现了由小到大的方位概念渗透过程。以第一学段《我的教室》作为“种子课”。教师在教学过程中可让学生以成语“四面八方”为联系点展开学习，通过“认识概念、建立表象—建构概念、实际感知—运用概念、建立模型”,在“四面”的认知中，习得这类模型的方法，用口头语言(与人介绍、视频介绍)呈现已获得的知识，建构初步的方位模型。到第二学段，教师继续以“四面八方”为联系点，让学生带着第一学段习得的方法进行“八方”的学习，通过自主学习及合作交流掌握本部分知识，用口头语言(与人介绍)、书面语言(制作藏宝图)呈现获得的模型，直观呈现思维成果。第三学段则在之前的基础上增加“比例尺”的学习内容，除了口头语言(与人介绍)、书面语言(制作平面图)外，还要突出评价的过程，对已有的模型进行归纳，建构知识系统。三个主题的模型逐级推进，有助于学生找到模型意识培养的学段进阶联系点，使其在逐步的建构过程中培养模型意识。

　　(二)单元整体衔接进阶培养点

　　对于学生思维的发展而言，重要的维度是思维的结构化和系统化。支持思维结构化和系统化的形成和发展，需要学习内容具有结构化、系统化。数学模型本身就是一种结构，需要教师从整体视角沟通知识之间的内在关联，有意识地选择、优化、结构化主题活动的素材，引导学生开展分类、对比、探究、交流、评价等数学活动，在活动中深入模型的本质，感悟模型思想。

　　以“欢乐购物街”主题活动为例，在以往的教学中，教师在完成关系模型和换算模型的建构后，一般会让学生自己到生活中体验购物，然后结束本部分学习。但在后期的反馈中，教师会发现多数学生并不善于运用“购物”中的数量关系模型，可见相关方法模型未得到充分建构。对此，在学生到生活中体验购物后，教师需进行第3学时的反思与评价(如图1),以突破课堂教学与实际生活的壁垒，引领学生经历“感悟模型—初步建模—运用模型—评价总结模型”的过程，完善模型意识培养机制。

　　二、主题学习活动化，在体验中发展模型意识

　　(一)活动化经历体验点

　　在小学阶段，学生的思维具有一定的局限性，这导致他们在进行严格意义上的建模活动时有较大的困难3]。为此，教师在学生已有经验和认知特点的基础上，通过自主探究、合作学习等，以跨学科活动化的形式，引导学生经历初步的简单模型建构、优化、运用的过程，可以逐步培养学生的模型意识，帮助学生积累初步的建模经验。

　　例如，在“校园平面图”主题活动中，多数教师会将目标聚焦于数学学科的教学，而学生容易就数学论数学，活动体验感不足，模型意识得不到充分培养。对此，教师可重新设计，组织“制作校园缩微景观沙盘”活动，具体步骤如下：第一，测量学校的长和宽，对比学校的长、宽和缩微景观沙盘的长、宽，选择最合适的比例尺；第二，运用正比例，用教学楼的影长算出微缩景观的高度(融入测量学、物理学的知识，进行数学史的渗透);第三，画出校园缩微景观图(与美术学科的立体构图主题相结合，突出数学与美术学科的融合);第四，完成校园缩微景观沙盘的创作，并分工进行介绍。

　　以上设计对“校园平面图”主题活动进行了丰富和完善，让学生以小组的形式分工协作，发现问题、分析问题、解决问题，能够促进学生在跨学科活动化体验中对比例尺和比例的概念模型形成更深刻的理解。

　　(二)故事化寻找落脚点

　　很多数学模型的形成经历了曲折而有趣的过程。教师在主题活动中，要注重引导学生了解数学模型形成的背景及演变过程，感受数学模型的价值。

　　例如，“度量衡的故事”主题活动以第一学段“身体上的尺子”的“身体尺”到“工具尺”丰富的感知为起点，设计了四个分主题：一是以一个小故事引出度量衡，初步感知模型；二是以“身体上的尺子”为基础，体验计量单位模型的建构过程，明确产生更精准计量单位的必要性；三是借助“不积跬步，无以至千里”“半斤八两”“才高八斗”等成语典故，理解长度、质量、容量单位模型，明确作用；四是以主题成果展，系统整合模型。整个主题活动可以让学生在中国传统文化中感知度量衡的由来，感受模型的历史，充分感知模型。

　　在教学中，教师与语文、美术、信息技术等学科融合，进行跨学科的单元整体主题活动，借助双师课堂，构筑跨学科融合的新样态，有利于培养学生的模型意识，深化学生对建模过程的了解，在文化支持下感受数学意义的建构与创生过程。

　　三、主题学习问题化，在应用中发展模型意识

　　数学发展是由问题驱动的。教师可以在主题式学习中进行体现数学思维脉络的、渐进性的、全方位的问题设计，为学生提供思考机会，并在思考过程中建构数学知识体系，让模型的建立水到渠成[4]。

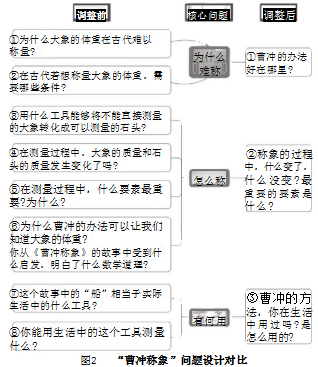
　　例如，在“曹冲称象的故事”主题活动中，教师可以从核心问题入手设置问题。如图2所示，调整前的八个问题对达成目标能够起到引领作用，但过于零碎的问题减少了学生自主思考的空间，因此，教师将其精简为三个大问题链。学生围绕问题思考，可以借助船体的吃水线，感受“大象的质量=排水量=相同排水量下石头的质量”,引导学生将不能直接测量质量的物体与可以直接测量质量的物体建立等量关系，形成解题策略，从而得到相同排水量下“大象的质量=石头的质量”这类关系，进一步认识“等量的等量相等”“总量等于各分量之和”这两个数学基本事实，发展量感和推理意识，向学生渗透转化的数学思想，以“曹冲的方法，你在生活中用过吗，是怎么用的”拓展课堂活动，深化模型建构，提高学生解决此类问题的能力。

　　四、主题学习反思化，在内化中发展模型意识

　　主题式学习尤其注重学生实践过程中的体验和感受，对自己参与活动时的思维、语言等认知活动进行监控和再认知，进一步形成模型意识5。教师通过处理已知条件、实现目标、克服障碍三个层面帮助学生进行反思，可以让学生在内化中发展模型意识。

　　选择性比较是处理已知条件的重要方法。通过选择性比较，学生可以发现新信息与已掌握信息之间的非明显关系。例如，在“欢乐购物街”中，教师可以指导学生把真实生活情境和已有的“元角分”模型进行对比，通过在问题中寻找和识别以前被忽视的相关信息，明确商品价格的不同呈现方式和购买方式；寻找和识别以前被忽视的信息组合方式，发现货币可以多种组合使用；寻找和识别以前被忽视的先前知识与问题情境之间的联系，感悟课堂上的买卖与实际生活中的买卖存在异同，从而发现生活实际给予的新信息与课堂上提供的情境在某些方面是相似的，然后利用这些信息在相似性的基础上形成心理表征，帮助学生利用新旧联系，更快地运用模型，解决问题。

　　教师可以引导学生利用“手段—目标”分析法、技能迁移法等实现对目标的分析。仍然以“欢乐购物街”为例，教师可以设计“不会用一会用—灵活用”三级评价量表，引导学生进行自我评价、合作评价，对目标完成情况进行反思。然后，教师对不同层次的学生进行分层指导，最后让学生再次尝试、反馈、反思，从而实现对模型的感知与运用，培养模型意识。

　　在教学过程中，教师要帮助学生克服障碍，用自己的思维反思。课堂教学应让学生有机会听到自己的解释并验证自己的推理，形成对具体策略的认识，减少对教师提供的信息的依赖。例如，在“校园平面图”主题活动中，教师结合不同的学时目标给出不同的反思框架，在测量环节后采用问题反思形式，引导学生对知识、方法进行反思，突出过程的反思，特别是“反思整个测量过程，你们觉得还有哪些细节是可以做得更简单、更省力的”,让学生对自己的测量方法进行优化，找到合适的测量方法，为建构模型奠定基础。在活动结束时，学生采用表格式的反思形式，突出“测量、记录数据”“画平面图”“整理汇报”等值得学习和改进的地方，从学科知识理解与运用、问题解决规划与操作、团队合作等主题式学习的角度进行反思。

　　五、结束语

　　综上所述，数学模型是用数学的概念、原理和思维方法去描述现实世界中具有规律性的东西，解决现实世界中的具体问题。数学模型可以使数学知识与现实世界接轨，构建数学与现实世界之间的桥梁。通过结构化、活动化、问题化、反思化的过程，教师可以让学生在主题式学习中感悟模型意识，提高学生用数学语言表达现实世界的能力。

　　[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京：北京师范大学出版社，2022.

　　[2]义务教育数学课程标准修订组.义务教育数学课程标准(2022年版)解读[M].北京：北京师范大学出版社，2022.

　　[3]王艳玲，吴正宪，马云鹏.跨学科主题学习设计与实施，小学数学[M].北京：教育科学出版社，2023.

　　[4]顾泠沅.数学思想方法[M].北京：中央广播电视大学出版社，2004.

　　[5]陈宇珊.模型思想在小学中高段数学教学中的渗透策略研究[D].成都：成都大学，2023.