摘要：学案导学是一种以学生自主或合作探究为主要形式的教学方式。自主、合作探究的过程离不开阅读、思考与表达。因此，作者进行了基于学案导学的初中数学“读思达”课堂教学实践研究。文章依据作者的研究成果，以“二次函数的概念”为例，从课堂导入、课堂讲解和随堂练习这三个环节入手，论述了引导学生进行“读思达”的策略，旨在让学生亲身体验数学学习过程，掌握数学知识，锻炼学习能力，发展核心素养。

　　关键词：初中数学；学案导学；“读思达”教学

　　学案导学是一种以学案为载体，以导学为主要方式，以学生自主或合作探究为主要形式，师生共同完成教学目标的教学方式。学案是教师引导学生进行自主或合作探究的重要工具。在此过程中，学生的阅读、思考、表达不可或缺。通过阅读，学生可以输入有价值的信息，建构初步认知；通过思考，学生可以加工有价值的信息，进一步巩固认知；通过表达，学生可以输出有价值的信息，强化已有认知。阅读、思考、表达三个环节并非孤立存在，而是相互联系且各有侧重的。值得注意的是，无论在哪个环节，学生都要发挥主观能动性，灵活运用各种方式进行探究。因此，在实施初中数学学案导学教学时，教师应将学案巧妙融入不同教学环节，有效引导学生进行自主或合作探究，使他们进行“读思达”。

　　一、课堂导入：利用学案引导阅读，输入信息

　　课堂导入环节是数学学案导学的第一个环节。在此环节，学生需要自主阅读学案，挖掘关键信息并认真思考，建构一定的认知。

　　在教学“二次函数的概念”时，教师设计出了如下自学案：

　　“二次函数的概念”学案之自学案

　　自读知识回顾和情境问题，思考问题，写下答案。知识回顾：

　　（1）在学习一次函数时，我们研究了哪些内容？

　　（2）我们从哪些方面研究了一次函数的性质？

　　问题情境：

　　经营着一家养殖场的老王想要用铁丝网为牛、羊做栅栏。在做栅栏的过程中，他遇到了一些问题。你能帮他解决这些问题吗？

　　（1）如果给羊做一个半径为R的圆形栅栏，这个栅栏的周长C是多少？面积S是多少？

　　（2）如果用长16 m的铁丝网给牛做一个长方形栅栏，这个栅栏的长是y m，宽是x m。你能写出y关于x的函数关系式吗？你能写出长方形面积与宽之间的函数关系式吗？

　　基于此，大部分学生会阅读自学案内容，并展开深入思考，从中提取出关键信息。同时调动知识储备，将新旧知识点联系起来，认真作答。

　　通过阅读、思考、表达，学生能够输入信息，顺利从已有知识过渡到新知，建构起对知识的全新感知。如一次函数的自变量的最高次项是一次，二次函数的自变量的最高次项是二次；因变量会随着自变量的变化而变化。同时，部分学生会主动发现并反思自身存在的问题，进而在后续课堂中更有针对性地与教师、同学一起探究。

　　二、课堂讲解：利用学案展开思考，加工信息

　　学案导学课堂的讲解环节是学生加工信息的环节。在此环节，教师要在了解教学重难点和学生自学情况的基础上，有针对性地进行指导，以此实现先学后教、以学定教。

　　（一）学生表达，教师指导

　　学生表达是教师了解学生学习情况的直接方式。在学生自主学习后，教师要给予他们表达机会，并运用适宜的方式进行针对性指导。

　　在学生完成自学案后，教师可以引导学生展示自学成果。学生代表会展示四个函数关系式：C＝2Rd，S＝πR2，y＝8－x，S＝8x－x2。基于此，教师可提出以下任务。任务一：观察这四个函数关系式，把握它们的共同点，并对其进行分类。任务二：与小组成员交流，结合一次函数的定义，提炼出另一类函数的概念。其中，任务一重在驱动学生探究一次函数和二次函数的特征，任务二重在驱动学生归纳二次函数的概念。在完成这两项任务的过程中，各组成员始终保持积极的思维状态，认真对比、分析、总结，获得一定的认知成果，并登台展示探究成果。

　　如，有小组提道：“形如y＝ax2＋bx＋c的函数是二次函数”。基于此，教师提出“a、b、c有什么特点？”“自变量的最高次数是多少？”“解析式有什么特点？”等问题。在问题的指引下，学生会继续思考，反复阅读二次函数的解析式，进而归纳出其特征，踊跃表达，如“a、b、c都是常数，但a不能是0”“自变量的最高次数是2”“解析式是整式”。如此，在整个过程中，学生在教师的指导下不断进行思考、表达，可以增强思维的灵活性和逻辑性，从而为探究重难点内容奠定基础。

　　（二）紧抓重难点，深入探究

　　重难点是学生必须掌握的内容。在初步认知新知后，教师要利用学案引导学生探究重难点内容。例如，一次函数和二次函数的区别与联系是本节课的教学重点之一。因此，在学生总结出二次函数的概念后，教师需要引导学生完成“二次函数的概念”学案之探究案。

　　“二次函数的概念”学案之探究案

　　任务：回想一次函数、二次函数的概念，对比、分析、总结出它们之间的区别和联系，完成下面的表格。

　　在完成任务的过程中，学生会主动联想一次函数和二次函数的概念，认真思考它们在表现形式、自变量的次数、系数要求上的区别与联系。

　　在学生自主探究后，教师使用白板展示一名学生的“二次函数的概念”学案之探究案。同时，教师鼓励其他学生对比自己与学生代表的表格内容，找出差异，并积极思考、分析。在对比过程中，学生会主动指出学生代表表格中的问题，并有理有据地分析问题，提出解决方案。同时，一些学生也会主动提出自己遇到的问题，而其他学生则认真思考问题成因并提出解决方法。最后，教师总结一次函数和二次函数的区别，并概述它们之间的联系。如此一来，全体学生可以建构正确认知，增强对二次函数概念的理解。学生在体验活动的过程中不断阅读、思考、表达，积累了学习经验，锻炼了学习能力，提高了学习效果。

　　三、随堂练习：利用学案进行表达，输出信息

　　随堂练习是学生在学案导学课堂上展示学习成果的环节。学生展示学习成果的方式有两种：一是解决练习题，二是梳理总结知识。

　　（一）设计解答类随堂练习

　　由于学生的学习兴趣、接受能力和认知水平存在差异，他们对数学知识的理解程度也不相同。因此，教师要在尊重学生个体差异的基础上，结合具体的教学内容，设计难度层次不同的解答类练习题，引导学生阅读、思考、表达。

　　例如，在讲解“二次函数的概念”后，教师围绕二次函数的概念设计难度不同的练习题，之后向学生发放“二次函数的概念”学案之练习案：

　　“二次函数的概念”学案之练习案

　　认真读题、细心分析，运用所学知识解决下列问题。（依据自己的水平选择相应难度的练习题）

　　基础练习：

　　（1）将y＝（3－5x）（4＋x）变成一般式，二次项是，一次项系数是，常数项是。

　　（2）观察：①y＝4x2；②y＝－2x＋4；③y＝100x2＋200x＋300；④y＝2x－1；⑤y＝x2－3/x＋4；

　　⑥y＝（x＋2）2－3x2。二次函数有（只填写序号）。

　　（3）已知函数y＝3x4m－5＋6。

　　①当m＝时，y是关于x的一次函数。

　　②当m＝时，y是关于x的二次函数。

　　能力提升：

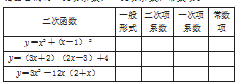
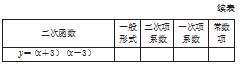
　　（4）将下面的二次函数转化为一般形式，并分别指出它们的二次项系数、一次项系数和常数项。

　　（5）一个矩形的周长是6 cm，面积y（cm2）和一边长x（cm）的函数关系式是。这是一个函数。

　　（6）已知y与x2成正比例，且当x＝－1时，y＝－3。求算：①函数y与x之间的函数关系式；②求当x＝4时，y的值；③求当y＝－1/3时，x的值。

　     拓展延伸：

　　（7）为了建设美丽校园，学校准备在操场上的一块一边靠墙（墙长25 m）的空地上开辟一个矩形种植园地ABCD。这个种植园地的一侧靠墙，另外三边用总长为40 m的栅栏围起来（如图1）。如果种植园地的边长BC为x m，种植园地的面积为y m2。求解：y与x之间的函数关系式，并写出自变量x的取值范围。

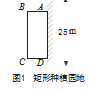
　　全体学生会在选定自己要完成的练习题后，边阅读边思考，分析题中的关键信息，得出答案。而后，学生代表主动讲解解题思路和答案。其他学生认真倾听，发现并指出问题，主动弥补自己的认知不足，进而提高认知水平。

　　（二）设计总结类练习

　　总结课堂所学是学生查漏补缺、强化已有认知的途径之一。在总结过程中，学生会回顾整个课堂学习过程，将注意力集中在关键知识点和探究方法上，从而明确自己学到了什么以及是如何学的。同时，学生可以发现自身存在的学习问题，并运用恰当的方式进行解决。在此基础上，学生可以运用思维导图、树形图、表格等形式展示学习成果，建构较为系统的认知。基于此，教师要在学案中设计总结类练习。

　　例如，在学生完成书面练习后，教师设计了“二次函数的概念”学案之总结案：

　　“二次函数的概念”学案之总结案

　　阅读“二次函数的概念”的自学案、探究案、练习案，回想本节课的学习过程，思考：（1）我学到了什么？

　　（2）我是如何学的？（3）我在学习过程中遇到了哪些问题？我是如何解决这些问题的？（4）我还有没有尚未解决的问题？我该如何解决这些问题？（5）学过这节课后，我最大的感受是什么？

　　根据自己的思考过程和思考结果，制作思维导图或树形图、表格，总结自己学到的知识和方法。

　　在思考过程中，大部分学生会在脑海中重构整个课堂学习场景，提取和总结知识点与学习方法，并通过绘制图表来清晰地展示学习成果，同时进行反思，发现自身存在的学习问题。基于发现的问题，学生会积极地运用阅读、对比、分析等方式来寻求解决问题的方案。随后，教师选择学生作品进行公开展示，并引导学生代表讲述知识和方法。教师认真倾听，发现问题，帮助其解决问题，继续完善学习成果。

　　四、结束语

　　总而言之，将“读思达”贯穿初中数学学案导学教学全过程，可以让学生真正获得自主或合作探究的机会，亲历数学学习过程。在此过程中，学生可以始终以学案为载体，运用恰当的方式进行阅读、思考、表达，扎实掌握数学知识，习得学习方法，提升学习能力，发展核心素养。在学生获得良好发展的情况下，基于学案导学的数学“读思达”教学效果也可得到提高。

　   参考文献：

　　[1]孙彩平.学案导学教学模式在初中数学教学中的实践与研究[J].数理天地(初中版),2024(3):92-94.

　　[2]陈芳,段振富.基于“读思达”数学学习模型的教学探索[J].数学之友,2023,37(14):51-54.

　　[3]黄玉霞.初中数学“读思达”课堂教学的实践与思考:以“三角形中边与角之间的不等关系”为例[J].中学数学教学参考,2023(8):20-22.

　　[4]胡惠颜,黄爱平.挖掘教材,培养学生的“读思达”能力[J].中学数学,2022(22):17-19.

　　[5]鲍淑香.学案导学教学模式在初中数学教学中的实践与研究[J].当代家庭教育,2022(6):93-95.