摘要：单元教学是撬动课堂转型的一个支点，大概念是单元教学的统领。在核心素养视域下，“大概念”“单元教学”备受一线教师关注。大概念统领下的单元教学已经成为培养学生核心素养的重要路径。因此，教师要把握初中数学日常教学时机，着力进行“大概念统领下的初中数学单元教学”研究。在研究过程中，教师应梳理大概念、单元教学的内涵，以此为指导，以课堂教学为依托，探索相关的教学路径与策略。文章依据部分研究成果，先论述大概念、单元教学的内涵，再以方程单元为例，介绍单元教学策略。

　　关键词：初中数学；大概念；单元教学

　　传统的数学课堂以“知识为本”，形成了“重知轻能”的教育现状，致使学生发展效果不佳[1]。《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）提出“设计体现结构化特征的课程内容”的课程理念，要求教师“对内容进行结构化整合，探索发展学生核心素养的路径”。大概念可以赋予单元教学实质意义，因此数学单元教学应以大概念为统领。

　　一、概念界定

　　（一）大概念

　　大概念是学科知识背后更为本质的、核心的概念或思想，建构了不同知识点或不同学科的纵横联系，具有主干核心性、逻辑结构性。大概念具有三种表现形式：（1）概念，指某类事物本质特征的抽象；（2）表现，指一种观点和看法，反映不同概念之间的关系；（3）论题，主要出现于人文艺术领域。一般情况下，大概念可以统领学科知识或不同学科知识，具有可持续的应用价值。

　　（二）单元教学

　　单元教学是以培养核心素养为出发点和落脚点，以整体思维为指导，以教材为基础，统筹、重组相关内容，获得一个相对独立的教学单元，以此为基础，创造性地实施教学活动。

　　（三）大概念统领下的单元教学

　　单元教学具有整体性。从知识本身来看，“整体”意味着知识之间有联系。学习的过程是建立知识联系的过程。在此过程中，大概念处于中心地位。从知识学习角度来看，“整体”意味着有意义建构。学习的过程是迁移应用认知，进行知识分化、重组、整合、改造的过程。在单元教学中，单元知识应当以大概念为中心，形成网状的知识结构。从课程角度来看，“整体”意味着统整。在大概念的引领下，单元要重新整合、设计。

　　二、大概念统领下的初中数学单元教学策略

　　（一）提炼大概念

　　提炼大概念是指明确大概念是什么，这是单元教学的前提[2]。如何提炼大概念？浙江大学教育学院刘徽教授总结了两条提取路径：一是自上而下地提取，即研读《课程标准》、核心素养提取大概念；二是自下而上地提取，即剖析知能目标、生活价值、学习难点、评价标准，理清大概念。教师要依据单元教学需要，采用适宜的路径提炼大概念。

　　例如，《课程标准》在“方程与方程组”“内容要求”中提到“能根据现实情境理解方程的意义，能针对具体问题列出方程；理解方程解的意义，经历估计方程解的过程”“能依据具体问题的实际意义，检验方程解的合理性”等。在实现如此种种要求的过程中，学生体验不同的活动，顺其自然地发挥抽象能力、运算能力、模型观念、应用意识。在数学学科核心素养的助力下，学生会解决方程问题。由此可见，解方程是方程单元的重点内容。在解方程的过程中，学生必须掌握方程思想。在掌握方程思想后，学生会走进具体情境中，迁移应用所学，列出方程、解答方程。所以，方程思想是方程单元的核心内容。于是，教师可采用自上而下的方式提取大概念——方程思想。之后，教师可以方程思想为中心，实施单元教学。

　　（二）表征大概念

　　表征大概念是指借助教学目标清晰地表征大概念。教学目标可以指明单元教学的方向。在清晰的教学目标的指引下，教师可以知道“教什么”“如何教”“教到何种程度”，一步步地落实大概念[3]。尤其，在整个教学过程中，学生不仅“会学”，还能“学会”，获得良好发展。对此，教师要站在整体角度，沿着“分析教材—洞察学情”这一路径，设定教学目标，清晰地表征大概念。

　　例如，北师大版初中数学教材在七、八、九年级分别设置了不同的方程内容，即一元一次方程、二元一次方程组、分式与分式方程、一元二次方程、在函数观点下研究一元二次方程等。其中，方程概念内容占六个课时，方程解法占十二个课时，方程的应用占十个课时，方程与函数占五个课时，回顾与思考占三个课时。可见，涉及方程的单元内容繁多，但重难点突出。重点内容是方程的解法，难点内容是方程的应用。方程的应用具有综合性，需要学生将方程思想作为工具，综合、运用不同的知识点，灵活解决具体情境中的方程问题。

　　但是，大部分学生往往对单元整体结构认知不充分，无法准确厘清不同知识点的内在联系。尤其，学生没有切实地掌握方程思想，在具体情境中很难解决实际问题。由此可确定，方程单元重在引导学生获取方程思想，把握知识联系，建构知识结构，解决实际问题。基于此，教师可以设定单元教学目标：（1）站在整体角度，系统把握不同知识点之间的关联，建构方程单元结构体系；（2）能建立有理数、实数、方程知识、运算方法、思想等之间的联系，搭建知识体系；（3）能灵活、准确地求解一元一次方程、简单的二元一次方程组、简单的一元二次方程，可以转化一元一次方程的分式方程，发展数学抽象能力和运算能力；（4）根据具体情境，运用方程思想，建立方程模型，解决实际问题，增强数学模型观念，提升数学运算能力和应用意识；（5）感受方程的应用，能在函数、平面几何等单元使用方程知识，灵活解决数学问题，培养数学运算能力和应用意识；（6）从算术思维发展为代数思维，灵活地解决实际问题，体会方程之间的转化，发展数学抽象能力。

　　（三）转化大概念

　　转化大概念是指将单元教学目标转化为核心问题[4]。解决核心问题的过程，正是学生学习单元内容、获取大概念、建构知识体系、发展核心素养的过程。核心问题是单元内容的共性概括。简单来说，核心问题是每一小单元均涉及的问题。明确核心问题，既可以增强单元教学的针对性，又可以使学生明确学习方向，积极探究，推动单元教学发展。因此，教师要分析各个小单元，发现共同内容，将其转化为大概念。

　　“方程与方程组”相关单元共由四个小单元构成——一元一次方程、二元一次方程组、分式与分式方程、一元二次方程。在学习每个小单元时，学生要认识不同知识的本质，了解不同方程的解法，把握不同知识点之间的联系，灵活应用不同知识点解决问题。基于此，教师可以设计四大核心问题，即“知识本质是什么？”“不同方程的解法有哪些？”“不同方程与其他知识点之间有怎样的关联？”“如何应用方程解决实际问题？”。

　　在方程单元教学中，教师将依据具体的小单元内容，提出核心问题，驱动学生使用多样的方式探究。学生通过解决核心问题，可以在掌握不同知识点的过程中，获取数学思想方法，建构知识体系，发展数学学科核心素养，由此实现单元教学目标，增强学习效果。

　　（四）落实大概念

　　1.设置问题情境，激发兴趣

　　单元教学倡导在情境中学习。问题情境是指教师在教学过程中有目的、有意识地提出问题，引导学生质疑问难[5]。有效的问题情境可以激发学生的探究兴趣，驱动学生积极探究。因此，在实施单元教学时，教师要先围绕小单元内容，创设有关的问题情境。

　　在一元一次方程小单元教学中，教师可借助电子白板向学生展示古希腊数学家丢番图的墓志铭（如图1)。

　　在学生诵读后，教师提出问题：“丢番图的年龄是多少岁？”教师给学生五分钟的思考时间。大部分学生积极思考，联想不同的知识点，使用不同的方式探究丢番图的年龄。在解决问题时，大部分学生列出算式，但算式解法烦琐。教师把握这个时机，引导学生思索简便方法。有部分学生提到列方程。于是，教师发问：“什么是方程？”学生迁移已有认知，介绍方程的相关内容。教师依据学生的作答情况，鼓励学生描述用方程求解丢番图年龄的方法。有学生说道：“设未知数x，列出方程，求解答案。”教师引导学生思考未知数的作用。如此一来，学生便可建立未知量和已知量之间的联系，初步感受划归思想。教师把握时机，介绍化归思想，并总结问题解决的流程（如图2)。

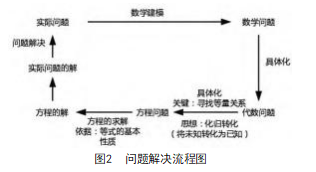
　　有效的问题情境能够驱动学生积极思维，迁移已有认知，建立方程与等式之间的联系。通过问题情境，学生能够初步感知学习方程的目的，感受算式与方程的差异，了解问题解决流程，感受化归思想，为深入探究方程小单元内容做好准备。

　　2.提出核心问题，深入探究

　　核心问题是小单元课堂教学的核心，能够推动小单元课堂教学发展[6]。在课堂讲解环节，教师要依据具体的教学情况，提出核心问题，驱动学生使用多样的方式进行深入探究，获得良好发展。

　　例如，在一元一次方程小单元课堂上，学生先后体验了探究活动，了解了方程的内涵和方程的分类。立足学生的探究所得，教师发问：“什么是一元一次方程？”学生在课堂认知的支撑下，联想到“一个未知数”“未知数的最高次数是1”，由此描述一元一次方程。依据学生描述的内容，教师发问：“像‘＋3＝5’这样的方程是一元一次方程吗？”学生回顾课堂所学，紧扣“一元一次方程的分母不含有字母”，给出否定回答。基于此，教师鼓励学生回顾代数式与整数式，认真类比，为方程分类。在分类的过程中，大部分学生了解了分式方程、整式方程等。于是，教师鼓励学生对比不同的方程，归纳一元一次方程的定义。有的学生说道：“只含有一个未知数，且这个未知数的最高次数是1的整式方程是一元一次方程。”教师趁机追问：“这个定义中的‘元’‘次’是什么意思？”学生结合自身的理解情况，踊跃作答。教师耐心指导，帮助他们完善认知。与此同时，教师呈现练习题，引导学生为方程分类。

　　学生在解决核心问题的过程中，始终积极思考，迁移应用已有认知，逐步了解了一元一次方程的概念，把握了不同知识点之间的联系，建构了知识结构。同时，在整个过程中，学生经过对比、判断、归纳，锻炼了数学抽象能力。

　　三、结束语

　　总而言之，教师有效实施单元教学，可以使学生在探寻大概念的过程中，扎实掌握每个知识点，把握知识点之间的联系，建构知识结构，顺其自然地发展数学学科核心素养，增强数学教学效果。

　　参考文献

　　[1]薛艳艳.学科大概念视角下的初中数学单元整体教学设计[J].智力,2022(25):131-134.

　　[2]司卫秀,徐丽.数学大概念视角下的单元教学设计:以“函数的概念与性质”单元教学为例[J].新课程导学,2022(16):22-24.

　　[3]庞嵘嵘.基于大概念的初中数学教学设计研究[D].桂林:广西师范大学,2022.

　　[4]孙丰.在初中数学教学中融入“大概念”[J].江西教育,2022(12):28-29.

　　[5]潘利英.核心素养背景下初中数学单元教学的有效设计方法探析[J].考试周刊,2021(98):85-87.

　　[6]张峰.初中数学单元教学的设计策略研究[J].新课程,2021(29):73.