[摘要]问题导学法是借助问题启发学生探究的教学方法，可以使学生通过探究、解决问题成为学习数学的主人，实现多方面的发展。《义务教育数学课程标准（2022年版）》强调数学教学应以学生为本，创设促进学生发展的活动。基于此，本文根据小学数学教学实施问题导学法的必要性，进行应用问题导学法实施小学数学教学策略的实践研究，在改进传统数学教学的基础上，推动学生获得良好的发展，增强数学教学效果。

　　[关键词]小学数学；问题导学法；问题教学

　　问题导学法是教师在生本教育理念的指引下，依据学生学情和教学内容，精心设计问题及在课堂上生成问题，借助问题启发学生自主、合作、探究的教学方法。《义务教育数学课程标准（2022年版）》（以下简称“新课标”）新课标提出“实施促进学生发展的教学活动”这一课程理念，要求教师利用启发式的教学方式点燃学生的学习兴趣，引发学生的积极思考，鼓励学生在真实情境中发现、提出问题，使用适宜的方法分析和解决问题，发展“四基”“四能”，逐步形成核心素养。问题导学法具有启发性，与新课标理念契合。通过应用问题导学法实施小学数学教学，可以使学生掌握数学学习主动权，发挥主观能动性与问题互动，自然而然地获得良好发展，切实扭转传统教学教师讲、学生听的局面。鉴于此，小学数学教师应当应用问题导学法实施数学教学，以“平行四边形的面积”为例，应用问题导学法的策略有以下几个方面。

　　一、前置课堂，设置问题

　　问题导学法以问题为中心，意味着教师要先设计有效的问题，夯实教学基础。有效的问题有三大特征：一是符合教材内容，二是契合学生学情，三是具有探究性和启发性。在数学课堂教学之前，教师要研读教材内容，确定核心知识，剖析学生学情，发挥教学智慧，设计具有启发性、探究性的问题。

　　“平行四边形的面积”是苏教版小学数学五年级上册第二章第一节的内容。本节课主要有四个知识点：运用转化法计算图形的面积；将平行四边形转化成长方形的方法；平行四边形面积计算公式的推导；平行四边形面积计算公式的实际应用。在学习本节课之前，学生在教师的引导下探究了长方形、正方形的面积公式，获取了方法，积累了经验，并且了解了平行四边形的特点及与长方形的关系，储备了解决实际问题的经验，发展了问题解决能力。在学有所得的情况下，学生可以体验平行四边形面积公式的探究活动。在此过程中，学生可以发挥主观能动性，探究方法、过程。但是，大部分学生此时没有掌握数学核心思想，在探究平行四边形的面积过程中遇到一些问题。基于学生学情和教学内容，教师设计四大核心问题。问题一：可以用什么样的方法计算平行四边形的面积？问题二：可以怎样将平行四边形转化为长方形？问题三：怎样推导出平行四边形的面积公式？问题四：如何应用平行四边形的面积公式解决相关问题？这四个问题串联整个课堂教学活动。同时，在教学活动实践过程中，教师将依据学生的学习表现，及时、有针对性地设置其他问题，启发学生不断探究。如此设置问题便于教师心中有数地实施课堂教学，减少教学的随意性、盲目性，增强课堂教学效果。

　　二、创设情境，提出问题

　　新课标指出了情境是发现、提出、分析、解决问题的依托。所谓的情境是教师在教学过程中使用手段、方式营造出的积极的情感氛围。在此氛围中，学生可以产生学习兴趣，认真观察、思考，发现且提出问题，有利于学生深入探究。因此，在课堂教学之初，教师要围绕教学内容，创设教学情境，让学生自主地发现、提出问题，推动课堂教学发展。

　　在“平行四边形的面积”这节课上，教师可以用生动的语言讲述地主给两个儿子分地的故事，将学生带入故事情境，同时结合故事内容，在电子白板上展现分给大儿子的①号地和分给小儿子的②号地（见图1）。

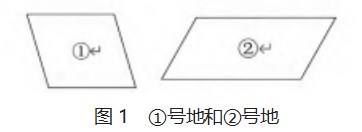
　　学生会根据故事内容，观察、比较两个平行四边形，产生不同的看法。有的认为①号地更大，有的认为②号地更大。面对不同的看法，学生自发提问：“到底哪一块地更大？”教师及时赏识学生的良好表现，并提出问题：“比较两块地的大小，实际上是在比较什么？”学生迁移已有认知，很容易联想到“面积”。此时，有学生提出问题：“要想计算平行四边形的面积，我们需要知道平行四边形的什么？”“我们可以怎样计算平行四边形的面积？”在一个个问题的作用下，学生纷纷开动脑筋，提出不同的设想，积极主动地探究。创设教学情境，不但使学生走进了数学课堂，还使学生活跃了思维，自主地发现、提出了问题，引出了新知内容，有利于推动课堂教学发展。

　　三、引导启发，探究问题

　　问题探究是问题导学教学的关键环节，有效的问题是教师启发学生的手段。在此环节，教师要始终关注学生学情，提出有效的问题，启发学生进行自主、合作探究。

　　（一）提出问题，启发学生自主探究

　　自主探究是学生彰显学习主体性，依据自身的亲身体验，使用自己的思维方式去探究的活动。在自主探究过程中，学生可以获得自由的时间和空间，大胆思考、表达。教师可以及时地了解学生的探究情况，有针对性地进行启发，促使学生走向探究深处，逐步地得出正确的结论。

　　例如，在“平行四边形的面积”课堂教学过程中，教师可以依托教学情境引导学生猜想平行四边形的面积公式。在学生自主猜想后，教师可以引导其展示猜想成果，就此提出一些问题，继续启发学生自主探究。具体地，有学生提到：“可以用邻边×邻边计算平行四边形的面积”。教师趁此发问：“用邻边×邻边得到的平行四边形的面积和平行四边形的实际面积相比，有怎样的大小关系？”学生会开放思维，提出不同的猜想。教师可以鼓励学生拉动平行四边形框架，得到一个长方形，感受面积是否发生了变化。在学生自主操作后，教师可以操作电子白板，将一个平行四边形框架转化为长方形，保留转化后的长方形和平行四边形的重叠图（见图2），帮助学生强化认知。

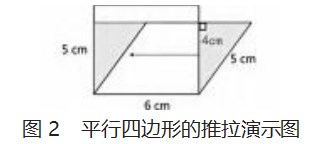
根据操作内容，引导学生判断“什么变了，什么没有变”。大部分学生结合操作过程和现象，很容易发现面积变了，但是周长没有变，并主动地讲述自己的发现和原因。在此过程中，学生意识到“不能用邻边×邻边计算平行四边形的面积”。在自主探究过程中，学生受到不同问题的启发，积极思维，认真观察、分析，逐步地得出正确的结论，建立深刻的数学认知。同时，在整个过程中，学生的思维更加活跃，在潜移默化中推理能力得到发展，自主探究水平得到提高，有利于增强课堂学习效果。

　　（二）提出问题，启发学生合作探究

　　合作探究是学生与小组成员通过合作交流、共同解决问题，得出结论，掌握知识，发展能力的活动。对于大部分小学生来说，数学复杂、抽象，很容易在自主探究过程中遇到一些问题。合作探究有助于学生减少探究问题，提高探究效率。在课堂教学过程中，教师可以依据学情，提出问题，启发学生合作探究。

　　例如，在启发学生验证“邻边×邻边”后，教师可以启发其验证“底×高”。在此次验证的过程中，大部分学生可以迁移课堂认知，联想到“将平行四边形转化为长方形”。教师可以顺势引导学生和小组成员一起动手操作，解决问题：能不能用“底×高”计算平行四边形的面积？在动手操作的过程中，大部分学生发散思维，提出不同的转化方法，一一实践，将平行四边形转化为长方形。教师把握时机，选取学生代表展示不同的操作方法，鼓励其他学生补充更多的方法。立足操作结果，教师询问学生：“在将平行四边形转化为长方形后，什么变了？什么没有变？”全体学生认真对比平行四边形和长方形，容易发现面积没有变，周长变了。教师赞赏学生的同时，追问：“为什么可以将平行四边形转化为长方形？”“为什么要沿着平行四边形的高进行剪切？”“转化前后的平行四边形和长方形各部分之间有怎样的关联？”受到一个个问题的驱动，学生主动地观察、分析，与小组成员进行交流，自主地建构良好认知。教师则可以根据学生的合作探究成果进行总结，促使其建立正确的认知。在问题的推动下，学生获得了合作探究机会。通过体验合作探究活动，大部分学生做到了知其然并知其所以然，既掌握了数学知识，还习得了转化思想，有利于建构良好的数学认知，增强了思维的灵活性、开放性，锻炼了推理、归纳能力，有利于提升学生的学习水平。

　　四、指向本质，解决问题

　　解决问题是指学生应用适宜的方式验证结论，把握知识本质。数学本质是学生必须掌握的内容，也是学生灵活运用数学的有力支撑。在课堂教学过程中，教师要在掌握学生学情的基础上，以知识本质为重点，提出问题，为学生获取探究方向，使用恰当的方式解决问题，掌握知识本质，深化课堂认知。

　　例如，在“平行四边形的面积”课堂教学过程中，学生在问题的启发下不断地进行探究，逐步总结出平行四边形的面积公式。面积的本质是度量。基于此，教师可以为学生发放一些格子纸，引导学生先用公式计算出其中的平行四边形面积，再使用数格子的方法数出平行四边形面积，验证计算结果是否正确。在学生得出正确结论后，教师可以强调面积的本质，帮助学生强化认知。在整个验证、解决问题的过程中，一些学生可以强化度量意识，提升量感。

　　五、随堂练习，实践问题

　　实践问题是指应用问题解决成果，解决其他的相关问题。简言之，实践问题是学生学以致用的活动。在此活动中，学生可以迁移课堂认知，分析问题，提取关键信息，利用适宜的方式厘清问题解决思路，列式、计算，得出结果。如此，学生既可以加深对所学知识的理解，还可以锻炼问题解决能力。需要注意一点，学生在个性差异的影响下存在明显的数学认知差异。教师可以依据学生学情和教学内容，分层设计随堂练习，驱动学生实践问题解决成果。

　　在“平行四边形的面积”这节课上，教师可以设计的随堂练习有：

　　【夯实基础】

　　1.一个平行四边形的相邻两边长是8厘米和6厘米。其中，一条底边上的高为5厘米。这个平行四边形的面积是（）。

　　2.将一个长方形框架拉成一个平行四边形。这个平行四边形的面积与原来的长方形的面积相比会（）。

　　【进阶提升】

　　1.下面是一些平行四边形的数据，请根据具体数据填写表格。

　　2.计算下面平行四边形的面积。

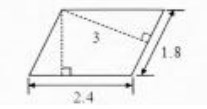
　　【拓展应用】

　　学校准备制作一个平行四边形宣传栏。这个宣传栏的底长12米，高4.8米。如果用油漆装饰这个宣传栏的表面，每平方米要用1.2克油漆。请问装饰这个宣传栏需要用多少克油漆？若每克油漆1.5元，装饰这个宣传栏需要花费多少元？

　　面对分层的随堂练习，每个学生都可以获得练习机会。在参与练习的过程中，学生可以迁移课堂认知，灵活应用平行四边形的面积公式，进一步加深认知。教师可以在学生解决练习题后，搭建讲评的舞台，鼓励不同学习水平的学生讲述解题思路、结果。在发现学生的解题问题后，教师可以有针对性地进行讲解，帮助学生完善认知，丰富解题经验。

　　综上所述，问题是启发学生探究的有力工具。在有效问题的启发下，学生可以主动地投身数学课堂，积极地体验数学教学活动。在体验活动的过程中，学生始终保持积极的思维状态，不断地思考、解决问题，由此掌握数学知识，习得数学思想，发展思维能力、问题解决能力、数学应用能力等，增强数学学习效果。问题导学法以问题为中心，注重启发学生，小学教师应当正确认知问题之于学生的影响，形成良好的教学意识，将问题导学法作为数学教学的重要工具，围绕具体教学内容，应用适宜的策略设置问题、提出问题、探究问题、解决问题、实践问题，形成数学教学的新路径，使学生在与问题互动的过程中获得一定的发展，从而提升数学教学质量。

      参考文献：

　　[1]潘兰.在小学数学“立学课堂”中开展“问题导学”的教学研究[J].小学生(上旬刊),2023(7):4-6.

　　[2]陈敏.以问促学以疑导学——问题导学策略在小学数学教学中的运用[J].学苑教育,2023(3):29-31.

　　[3]王翠.浅谈问题导学法在小学数学教学中的应用[J].数学学习与研究,2022(32):17-19.

　　[4]刘茂光.小学数学课堂教学中“问题导学”模式的实践运用[J].天津教育,2022(22):74-76.

　　[5]王永红.关于小学数学教学中“问题导学”模式应用的探究[J].数学大世界(下旬),2022(4):29-31.