[摘要]本文赏析了特级教师徐长青“多边形的再认识”一课，在教学中，通过带领学生回忆旧知，帮助学生复习多边形的特征；由旧到新，帮助学生拓展多边形的定义；尝试多种途径，引导学生探究多边形的转化；大胆自主探究，促进学生发现通用的面积公式；将数形相结合，帮助学生勾连公式的不同应用；最后通过全课总结，交流、提升本堂课的体会和认知。这节数学课虽然是一节复习课，但是高效实现了学科知识与学科活动的融合，“做中学”与知识融为一体，让学生在具身认知和思维可视化中成长。

　　[关键词]多边形再认识；数形结合；具身体验

　　在第34届现代与经典全国小学数学教学观摩研讨会上，数学特级教师徐长青展示了“多边形的再认识”一课，他在课堂上关注学生的具身认知，借助“数学手臂操”激活学生的生理体验和心理感觉，让学生开心地学习；关注学生的思维可视化，让学生在数与形的想象和转化中认识多边形之间的内在联系。看似简单的教学活动，其实每一个任务都不断启发学生数学思考，在相互的讨论和交流中碰撞出思维的火花，促进学生更加深刻地理解数学知识，发展学生的核心素养。

　　一、回忆旧知，复习多边形的特征

　　【教学片段】

　　师：同学们，看到“多边形”这三个字，你头脑中出现了哪些学过的图形？

　　生：我们学过的有长方形、正方形、平行四边形、梯形和三角形。

　　师：（出示已经学过的平面图形）说得真全，我们一起在屏幕上找一找你们学过的图形在哪里。

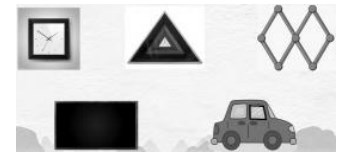
       生：我在第一幅图中看到了正方形，正方形的四条边长度都相等。如果四条边都是a，正方形的面积是边长乘边长，周长是边长乘4。我在第二幅图中看到了三角形，三角形的内角和是180°,三角形的面积是底乘高除以2，三角形的周长是三条边的长度相加。我在第三幅图中看到了两个平行四边形，它的特征是有两组相等且平行的边，平行四边形的面积是底乘高，平行四边形的周长是四条边的和。

　　师：我要问你一个问题，三角形具有稳定性，平行四边形具有不稳定性，你能解释下为什么吗？

　　生：拉动三角形后仍然是三角形，所以三角形具有稳定性。拉动平行四边形后有可能不再是平行四边形，所以平行四边形具有不稳定性。

　　师：下一幅图看到什么了？

　　生：我在第四幅图中看到了长方形，长方形的特点是有两组对边平行且相等，长方形的面积是长乘宽，长方形的周长是长加宽的和乘以2。

　　师：你说得很全面，我们用a表示长方形的长，用b表示长方形的宽。请你用一句话来表示长方形和正方形的关系。

　　生：那说明正方形是一个特殊的长方形。

　　师：还有一幅图，你能说出梯形的哪些知识？

　　生：梯形的面积是上底与下底的和乘高除以2，梯形的周长是上底加下底，再加上它两边的腰。

　　师：同学们，刚才我们把学过的五个图形都回忆起来了，它们是一家子的，叫作“多边形”。

　　【赏析】复习旧知是数学学习中必不可少的，这不仅能帮助学生巩固所学的基础知识，还可以帮助他们更加深入地理解数学概念和原理，从而更好地掌握数学思想和方法。同时，复习旧知是学生必须养成的一种良好的学习习惯，可以让他们在学习其他学科时受益。徐老师通过提问唤醒学生学过的多边形旧知，再在呈现多种图形中说出每个多边形的特征、面积和周长计算公式。

　　二、由旧到新，拓展多边形的定义

　　【教学片段】

　　师：同学们，刚才五个多边形中大多数是四边形，有一个是三边形。你知道三角形是怎么构成的？

　　生：三角形是三条边首尾相接围成的一个图形。

　　师：说得不错，三条边没围之前只能叫线段，围完之后它才叫边。那什么是四边形？

　　生：四条线段首尾相连的图形叫四边形。师：那五边形呢？

　　生：五条线段首尾相连的图形叫五边形。师：那n边形呢？

　　生：由n条线段首尾相连围成的图形叫n边形。

　　师：同学们，我们每天学习的课程是有限的，但是给了我们这条有限的线索，我们就可以用它去解读更多的类似问题，可以去推演出多边形的定义，你们刚才已经做到了，要把掌声送给我们自己。

　　【赏析】数学学习是一个逐步发展和深化的过程。教师带着学生从已有的旧知识出发，回顾三角形的定义，体现到封闭图形是按顺序首尾相连围成的平面图形。接着，学生进一步拓展到多边形的定义，体会到用有限的线索解决更多类似的数学问题。从基础的传统多边形到更广泛的多边形，多边形的定义是对传统多边形的拓展和延伸。通过不断扩展多边形的定义，我们可以更好地理解和研究各种几何对象，探索更广泛的数学领域。

　　三、多种途径，探究多边形的转化

　　【教学片段】

　　师：这节课学习的是“多边形的再认识”，我们认识了五个图形，也学过了这五个图形的面积计算公式，让我们再回忆一下。长方形的面积是a乘b，正方形的面积是a的平方，三角形的面积是a乘h除以2，梯形的面积是a与b的和乘h除以2。刚才我们在研究图形的时候，如果梯形两条底的长度相同，两条腰的长度相同，变成什么图形了？

　　生：可能是长方形，也可能是正方形，还可能是平行四边形。

　　师：平行四边形什么时候才能变成正方形？生：不仅要a等于b，还要a等于h。

　　师：今天我就想让这一家子和大家见一次面，看一看梯形变形、正方形变形、长方形变形、平行四边形变形、三角形变形，可以吗？（出示梯形）谁能移动它的点把它变成三角形？（学生展示）成功了，你发现变成三角形以后，哪儿消失了？

　　生：它的上底消失了。

　　师：谁能把这个三角形变成平行四边形？（学生展示）谁能把这个平行四边形变成长方形？（学生展示）谁能把这个长方形变成正方形？（学生展示）既然是一家人，那我们今天就从一家人的角度去认识它们，用我们的身体形象地表示出它们之间的关系。（教师示范，学生跟着做）先表示长方形，能想象出来吗？……（教师边示范，边总结口诀）双臂立直是图形，左右拉伸长方形，左右拉伸长方形。拉到长和宽相等，它就变成正方形。继续拉伸回到长方形，双臂摇摆就变形，同步摇摆四边形，异步摇摆变梯形。指尖合拢三角形，指尖合拢三角形，指尖合拢三角形。

　　师：太好玩了，慢慢地把数学知识刻到我们身体里面，好记吗？

　　生：好记。

　　【赏析】在数学中，多边形的转化是一种常见的解题策略，它可以通过各种途径实现。探究多边形的转化有助于我们更好地理解几何图形的性质和关系，提高解决几何问题的能力。徐老师首先带领学生再次回忆了五个多边形的面积计算公式，同时启发学生思考梯形两条底的长度相同和两条腰的长度相同时会变成什么图形。接着，徐老师利用睿知云交互式教学工具，让学生通过移动把梯形变形、正方形变形、长方形变形、平行四边形变形、三角形变形，直观地看到多边形之间的转化。最后，徐老师层层追问引导学生自编数学手臂操，在朗朗上口的口诀中进一步记忆多边形之间的转化关系。

　　四、自主探究，发现通用的面积公式

　　【教学片段】

　　师：同学们，我们发现这么好的五个兄弟出现了五个面积计算公式，它们能不能用一个面积公式就解决这五个图形的所有面积问题呢？

　　生1：我发现有几个图形的面积公式是有联系的，除了三角形外，其他都是四边形。我可以用两个相同的三角形拼出其他的四边形……

　　生2：我觉得如果这些图形的底和高相等，可以用长方形的面积减它们不到长方形的地方……

　　生3：我认为三角形面积公式可以，用三角形面积公式可以推算出长方形的面积公式……

　　生4：请大家看三角形，我们把这个三角形最上面这个点看作0，那么这个三角形的面积就是用0与a的和乘高除以2，就跟这个梯形的面积一样了。请大家看平行四边形，平行四边形的上底和下底都是a，所以平行四边形的面积是a与a的和乘高除以2，化简之后就是ah。请大家看正方形，正方形的上底、下底、高都是a，所以正方形的面积是a与a的和乘a除以2，化简之后就是a的平方。请大家看长方形，长方形的上底和下底都是a，所以长方形的面积是a与a的和乘b除以2，化简之后是ab。

　　师：掌声送上。同学们，学习就是敢于跳出原有的认识，从另一个数学的角度去看它。当你看完之后，突然发现它又回来了，我们从另一个角度把它视为梯形的状态，又推倒回了原有的图形的公式。看起来无论怎样变化，万变不离其宗。你看，当我们把梯形上底的指尖合拢变成三角形的时候，它的上底自然就变成了0，可以把这五个兄弟都统一成梯形的面积公式。

　　【赏析】徐老师继续引导学生探究五个多边形之间的转化关系，引导学生寻找一个面积公式解决这五个图形的面积问题。一开始，学生只是发现能用一个面积公式解决两个或三个多边形的面积问题，后来学生突然受到“指尖合拢三角形”的启发，顿悟到可以用梯形的面积公式解释其他四个多边形的面积公式，从而找到了多边形的通用面积公式。

　　五、数形结合，勾连公式的不同应用

　　【教学片段】

　　师：（出示题目：1＋2＋…＋99＋100）同学们，谁能快速地告诉我这道题目的得数是多少？

　　生：5050。因为这一串数字是等差数列，用首项加末项乘以项数，再除以2就可以算出来。也就是1与100的和乘100除以2等于5050。

　　师：等差数列，你都知道了啊，这是课外知识呢！（出示题目：1＋2＋…＋9＋10）同学们，请你算一算这道题目。

　　生：1与10的和乘10除以2等于55。

　　师：（出示等差数列公式和梯形面积公式）等差数列公式与梯形面积非常像，你看出来了吗？

　　生：首相可以看作上底，末项可以看作下底，项数可以看作高……

　　师：这个等差数列公式我怎么没有看到梯形呢？（出示题目：3＋4＋5＋6＋7）你能结合这道题画个图吗？

　　生：第一行有3个圆片，第二行有4个圆片，第三行有5个圆片，第四行有6个圆片，第五行有7个圆片，就能画出一个梯形。我们可以这样计算：上底3加下底7乘高5等于25。

　　师：掌声送给这位同学，有的同学把它画成了直角梯形，有的同学把它画成了等腰梯形。无论怎样，我们发现梯形的面积公式和等差数列的公式非常像。

　　【赏析】数形结合是一种重要的数学思想，它通过将抽象的数学概念与直观的图形相结合，帮助我们更好地理解数学问题。在数学中，有很多公式可以通过数形结合的方式进行解释和应用，例如，等差数列公式、梯形面积公式等。如果把引导学生发现多边形的通用面积看作从形到数，那么学生根据等差数列的算式画出梯形的过程就是从数到形。数与形的有机结合，不仅让学生感受到等差数列公式与梯形面积公式之间的对应关系，也体会到等差数列公式看似是课外知识，其实是对课内知识的深化。通过数形结合的方式，学生可以更好地理解公式的含义和应用，从而更好地解决数学问题。同时，数形结合还可以帮助学生发现新的数学规律和性质，推动数学的发展。因此，数形结合是一种非常重要的数学思想和方法。

　　六、全课总结，交流数学课堂的体会

　　【教学片段】

　　师：其实所谓的课外知识本来就是我们课内的，只不过我们再向前走一小步就将与它遇见，但是很多人很少走这样的一小步，所以我们对一个图形的学习往往不是一蹴而就的，而是在认识中才有新的提升。因此，我们不要固化在昨天的一节课里，应该把每节课学的知识还原到它的一个知识家族里面，再看它的时候你会有不一样的感觉。那这节课你还是孤立地理解长方形、正方形、平行四边形、三角形和梯形吗？同学们，这节课有什么收获呢？生1：除了收获多边形的面积公式，我还理解了面积公式是怎么来的。梯形面积公式可以表示其他多边形的面积，梯形面积公式还和等差数列公式有联系。

　　生2：我收获了凡事可以用另一个角度去看，那你会发现更多的知识。

　　……

　　师：同学们，数学的视角不是单一的，它是多维的。随着知识的学习，我们的视角应该越来越丰富。今天我们站在整体的视角再看每一个图形……

　　【赏析】数学课堂不仅是一个传授知识的场所，更是一个全方位提升学生核心素养，锤炼思维品质，培养科学精神的重要舞台。在课末，教师组织学生交流整节数学课的学习收获，有的学生从知识的角度讲述了自己学到的数学知识，也有的学生从能力的角度讲述了自己学到的看待问题的视角与方法，也有的学生从素养的角度讲述了数形结合思想方法的广泛应用。

　　总之，“多边形的再认识”既是一节新授课，也是一节复习课：“新”在让学生看到了数形结合在多边形面积和等差数列中的应用；“旧”在学生已经单独学习过每课时的平面图形面积计算，这节课只不过是把这五个多边形串联在一起。在整节数学课中，徐老师巧妙地设计学生活动，将学科知识与学科活动融为一体，“做中学”活动与知识融为一体，数与形融为一体，并且给予全班学生充分的具身体验和数学思考时间，帮助他们在一次次思考与卡顿中实现顿悟性学习，促进学生会用数学的眼光观察世界，会用数学的思维思考世界，会用数学的语言表达世界。

      参考文献：

　　[1]钱建兵.把握图形概念特点,发展几何思维—“第二学段多边形认识”教材比较及教学启示[J].中小学教师培训,2021(12):59-63.

　　[2]刘琳娜,李慧丽.整合学习任务,实现图形认识与测量的一致性“多边形周长”教学思考与实践[J].小学数学教师,2022(11):24-28.

　　[3]朱忞,金妤茜.把握概念本质实现整体建构—“多边形的初步认识”教学实践与思考[J].小学数学教育,2022(18):67-69.