2022年中考是落实“双减”政策后的首次中考，疫情多点频发的双重压力给今年的初三教学特别是备考工作带来更多困难与挑战。面对诸多不利因素，更需要师生共同直面挑战，积极应对。教师要尽力做到一生一策，给予学生更多个性化学习辅导，指导他们稳住自己的复习节奏；学生自己也要学会自主与自律，提高居家线上复习的有效性。只要师生无惧挑战，抓住机遇，定会发挥出自己应有的水平。

　　一、关注课改动向，复习有方向

　　《义务教育数学课程标准(2022年版)》明确提出：要关注数学学科发展前沿与数学文化，继承和弘扬中华优秀传统文化；与时俱进，反映现代科学技术与社会发展需要；符合学生的认知规律，有助于学生理解、掌握数学的基础知识和基本技能，形成数学基本思想，积累数学基本活动经验，发展核心素养。上述数学学科的育人功能值得师生关注。比如，朝阳二模出现的试题中出现的汉字之美和围棋，就是很好的数学学科与传统文化相融合的问题：

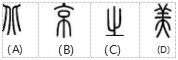
　　例1汉字是迄今为止持续使用时间最长的文字，是传承中华文化的重要载体。汉字在发展过程中演变出多种字体，给人以美的享受。下面是“北京之美”四个字的篆书，不能看作轴对称图形的是()

　　例2围棋是一种起源于中国的棋类游戏，在春秋战国时期即有记载，围棋棋盘由横纵各19条等距线段构成，围棋的棋子分黑白两色，下在横纵线段的交叉点上．若一个白子周围所有相邻(有线段连接)的位置都有黑子，白子就被黑子围住了。如图1，围住1个白子需要4个黑子，围住2个白子需要6个黑子；如图2，围住3个白子需要8个或7个黑子。像这样，不借助棋盘边界，只用15个黑子最多可以围住_____个白子。

　　二、关心社会热点，把握新情境

　　2022年北京各区的一模和二模试题中，出现了一些新名词，例如，科技创新指数、科技创新效益指数，同比、环比，工况、能耗等。这些新名词的出现，旨在引导学生关心时事、社会热点，培养学生数学阅读和问题解决能力。

　　例如，平谷二模的第7题，讨论的是纯电动汽车低速工况和高速工况的能耗情况，学生在这里要会的是利用图像，比较平均数和方差，而“纯电动汽车低速工况和高速工况的能耗情况”对学生来说，是陌生的概念和问题情境。

　　例3测试某款纯电动汽车低速工况和高速工况的能耗情况，为了更接近真实的日常用车环境，低速工况的平均时速在30km左右，包括城市一般道路、环路等路况；高速工况的平均时速保持在90km左右，路况主要是高速公路。设_低速工况时能耗的平均数为x1，方差为s；高速工况时能耗的平均数为2，方差为s，则下列结论正确的是：

　　三、重视回归教材，基础再夯实

　　根据以往复习备考经验，笔者认为，越是到复习的冲刺阶段，师生越要特别重视基于考试情况回归教材本身，回归并深化数学概念、定理、公式和法则的本质理解。例如，人教版教材九年级上册二次函数第51页探究3中的问题，和顺义二模中的第24题所给问题抛物线形拱桥的截面图类似。

　　例4(顺义二模24题)如图是某抛物线形拱桥的截面图。某数学小组对这座拱桥很感兴趣，他们利用测量工具测出水面AB的宽为8米。设AB上的点E到点A的距离AE＝x米，点E到拱桥顶面的垂直距离EF＝y米。

　　通过取点、测量，数学小组的同学们得到了x与y的几组值，如下表：

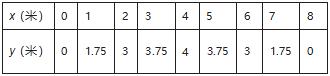
　　(1)拱桥顶面离水面AB的最大高度为______米。

　　(2)请你帮助该数学小组建立平面直角坐标系，描出以上表中各对对应值为坐标的点，并用平滑的曲线连接。

　　(3)测量后的某一天，由于降雨原因，水面比测量时上升1米。现有一游船(截面为矩形)宽度为4米，船顶到水面的高度为2米。要求游船从拱桥下面通过时，船顶到拱桥顶面的距离应大于0.5米。结合所画图像，请判断该游船是否能安全通过：______(填写“能”或“不能”)。

　　将教材中的例题练习和模拟试题进行对比研究，我们可以看到，该试题与教材中利用待定系数法求得解析式，然后解决实际问题的设问方式是一致的，且实际背景也一样。不同的是模拟试题的设问加入了取点、测量，读取表格信息，之后再描点画图，选取合适的点求得解析式，最后落到实际问题的解决。模拟试题中整个问题的设问体现了整个函数学习过程，那么我们再重温教材的时候不妨对某些练习进行改编，让学生在熟悉的问题中不断深入思考，加深对问题的理解。

　　再如，人教版教材数学九年级上第36页例4，与石景山二模第24题进行对比，参考试题中的问题设置方式我们还可以对例题进行如下改编。

　　例5石景山二模24题某公园内人工喷泉有一个竖直的喷水枪，喷出的水流路径可以看作抛物线的一部分，记喷出的水流距喷水枪的水平距离为xm，距地面的竖直高度为ym，获得数据如下：

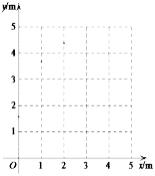
　　小景根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究。

　　下面是小景的探究过程，请补充完整：

　　(1)在平面直角坐标系xOy中，描出以表中各对对应值为坐标的点，并画出该函数的图像。

　　(2)水流的最高点距喷水枪的水平距离为m。

　　(3)结合函数图像，解决问题：公园准备在距喷水枪水平距离为3.5m处加装一个石柱，使该喷水枪喷出的水流刚好落在石柱顶端，则石柱的高度约为m。从上面例子不难发现，抛物线表达式y=a(x−h)2+k，a、h、k是其中的待定系数，a确定抛物线开口大小，通过改变出水的角度可以改变a的大小，x=h是对称轴，图像横向平移可改变，k是图像的最高点纵坐标，图像纵向平移可得，所以可以进行如下设问：

　　设问1：增加水管的高度，水柱落点位置怎样改变？

　　设问2：移动水管的位置，水柱落点位置怎样改变？

　　设问3：改变出水口的压力方向，水柱落点位置怎样改变？

　　通过对课本原例题和模拟试题结合的再设计，可以获得如下教学效果。一是从学生熟悉的问题背景出发，促使学生体会到不少问题就源自我们学习过的例题或练习，帮助学生树立数学学习的自信心。二是通过对例题进行变式，帮助学生理解此类问题的实质，即从三个待定系数角度设问，利用待定系数法确定图像等，让学生通过不同问题的解决获得通性通法。三是，在完成此类问题的过程中，完成了函数整个学习过程的再复习——描点、画图、连线、选点确定函数解析式，最后到解决问题，实现一题多用，达到减负提质的教学目标。

　　综上所述，在中考备考复习过程中，理解课标要求，明确备考方向；关心社会时事，紧跟时代步伐；回归教材本身，理解数学本质，落实减负提质，帮助学生有的放矢地积极准备，必能在中考中取得理想成绩。