摘要：在现代农机零部件的生产加工过程中，数控技术的合理优化也是提升此类零部件生产加工效率及其质量的关键措施。基于此，研究者与技术人员应结合实际情况，采取合理的策略来优化此项技术，并通过实践应用的方式来判断其应用效果。本文主要研究了农机零部件加工中的数控技术优化与应用策略，包括数控技术及其在农机零部件加工中的应用优势，农机零部件加工中的数控技术优化策略及其优化策略的实践应用分析。经分析可知，在对农机零部件进行加工的过程中，数控技术的主要优化策略包括优化变量、优化算法以及优化解集等。而在经过优化之后，其加工效率、精度及其节能效果都将得到进一步提升。希望通过本次的分析，可以为数控技术的合理优化与农机零部件加工效果的提升提供一定参考。

　　关键词：农机零部件；数控技术；优化变量；优化算法；优化解集

　　1数控技术及其在农机零部件加工中的应用优势

　　1.1数控技术

　　数控技术就是借助于数字信息来控制机械运动的一种先进技术，该技术融合了计算机、机械制造、传感检测、现代控制、光机电以及网络通信等多种现代制造业中的先进技术，具有柔性自动化、高效率以及高精度等的特征[1]。目前，此项技术已经在机械制造领域中得到了广泛应用，尤其是在机械零件加工领域中，该技术及其应用更是备受关注。

　　1.2应用优势

　　就目前的农机零部件生产加工领域来看，数控技术在其中的主要应用优势表现在以下几方面：（1）可进一步提升其生产加工效率，因数控机床的切削用量较大，可显著缩短加工时间，且在自动化技术的支持下，其辅助时间也可以显著缩短，从而具备更高的加工效率。（2）可进一步提升其生产加工精度，数控机床的综合性很高，是由很多精密机械设备与自动化控制系统共同组成，其定位与重复定位精度都非常高，整体刚度与热稳定性很好，因此可在实际加工中达到更高的加工精度。（3）具有更高的经济效益，因数控机床中的很多工序可集中实现，具备一机多用的特征，且在自动化技术的支持下，该技术的应用也可以省去更多的人力成本，从而具有更高的经济效益。

　　2农机零部件加工中的数控技术优化策略分析

　　在当前我国的农机零部件数控加工中，涉及的零部件通常都具有较大的复杂度，这就为其数控加工带来了较大挑战。而在具体的加工过程中，数控机床的主要优化需求不仅仅局限在其加工效率和加工精度的提升，同时也需要进一步节约其运行能耗，延长切削刀具的使用寿命。这样才可以使此项加工工艺更加符合当前的绿色节能与可持续发展目标，从而为农机零部件数控加工技术及其生产制造领域的发展提供技术支持。基于上述目标，在对农机零部件进行生产加工的过程中，数控技术的主要优化策略通常包括三种，一是优化变量，二是优化算法，三是优化解集[2]。基于此，本次便以农机零部件数控加工机床中精英策略条件下的非支配排序遗传算法（以下简称NSGA-II算法）作为主要的优化算法，对其在农机零部件数控技术中的优化策略进行分析。

　　2.1优化变量

　　在对农机零部件数控加工机床进行技术优化的过程中，优化变量的合理选择至关重要。只有做好各项优化变量的选择与控制，才可以使此类数控机床的生产加工参数得到更加合理的优化，并使各项参数之间达到良好的配合效果，以此来提升其整体优化质量。就目前来看，农机零部件数控加工中的主要参数有四个，第一是主轴转速，通常用n表示；第二是每齿进给量，通常用fz表示；第三是径向切削深度，通常用ae表示；第四是轴向切削深度，通常用ap表示。基于此，在具体的优化变量选择中，研究者可将上述四个参数用作优化变量，在确保零件的表面加工精度及其质量的基础上，尽最大可能降低加工中的热损耗和能耗，并使数控机床中的刀具具有更长的使用寿命。为达到这一目标，研究者可按以下优化模型函数来进行优化：

　　其中，Fm代表数控铣削加工中的能耗量，其单位是kJ。

　　2.2优化算法

　　针对农机零部件生产加工中的数控机床，在对其实施技术优化的过程中，优化算法的合理应用是确保其优化效果的关键措施。基于此，研究者一定要结合此类机床的实际情况，将当前典型且常见的优化算法合理引入其中，并在此类算法的支持下完成其中的各项参数优化。在当前，NSGA-II算法属于多目标优化算法中的一个经典算法，该算法是在NSGA（传统非支配排序遗传算法）基础上进行的扩展与改进，将一些智能化的算法技术与算法策略合理应用其中，使其具备足够强大的能力来进行多目标优化，同时也使其具备了比较强大的高效收敛以及全局搜索等能力。

　　在该优化算法的执行过程中，首先会随机生成一个父代种群，此处用P0表示，通过选择、交叉以及变异等的算子再生成一个子带种群，此处用Q0表示，其个数均为N。然后对父代和子带种群进行合并，从而得到一个全新的种群，此处用R0表示，其个数为2N。之后通过非支配排序法来操作R0种群，使其被划分成多个非支配层级的形式，此处用Zi表示，其中的i为1,2,3，……，n。在对其进行非支配排序时，该算法会将个体之间的实际支配关系作为依据，按照不同个非支配层次对其进行划分，越低非支配层次中的个体就越优秀。对于其中的每一个非支配层级Zi，需要对其个体之间所具有的拥挤度进行计算，以此来衡量其中不同个体之间的具体分布情况，通过对不同个体多样性的维护，便可使种群具备良好的多样性与均衡性特征。之后再对非支配层级Zi里的优秀个体进行选择，将其放到新生成的父代种群里，此处用P2表示。当前的这个父代种群F2数量如果没有达到N个，该算法系统会继续对下一级非支配层级Z2里的个体放入P2，一直到其数量达到N个。如果其中的非支配层级数量在N个以上，超出N个的部分用Zm表示，研究者就需要通过比较拥挤度的方式来决定个体保留情况。在此过程中，拥挤度比较算子会将非支配层级里的相应个体拥挤度数值作为依据，对其优劣度实施降重处理，将最优个体保留下来，将其他个体淘汰掉[3]。通过这样的方式，便可有效存留种群中的高质量解，并使其具备良好的多样性特征。最后是对保留的个体进行非支配排序，即对候选解在多目标函数中的优劣实施排序处理，并按不同级别对其进行划分，让同一级别中的不同解互不支配。通过这样的方式，便可找出最优解所组成的集合，从而为农机零部件生产加工中的数控参数设置提供有利的参考依据。

　　2.3优化解集

　　针对农机零部件生产加工中的数控机床设备及其系统，在具体的技术优化过程中，研究者需要将通过优化算法获取到的解集作为依据，采取合理的措施对其解集实施进一步的优化处理，以此来提升其优越度，使此项技术的优化效果达到最佳，从而使数控机床达到最佳的运行状态。在采用非支配排序法对优化解集进行排序之后，上述算法种群里的个体会按不同非支配层级被重新划分，每一个层级里的不同个体都不能相互支配。而在具体的非支配排序时，对于所有的个体，该算法都将会按照其在多目标函数模型中的具体优劣情况来进行排序，对于较其他所有个体都优越的个体，该算法会将其排列在第一层；对于较除第一层以外所有其他个体都优越的个体，该算法会将其排列在第二层，后续的排列方法均依此类推。在经过非支配排序之后，便可获得比较优越的一组算法解集，该组解集在不同目标条件下获得的性能将相对均衡，从而产生一个新的解集，研究者将其叫作帕累托前沿解集（以下简称Pareto解集）[4]。在Pareto解集中，为使不同个体在其前沿上的分布情况足够均匀，研究者需要将拥挤度计算引入到NSGA-II算法中。其中的拥挤度主要用来对目标空间里的个体密度进行衡量，以此来确定不同个体的相对距离[5]。在实施了拥挤度计算之后，该算法便可使Pareto解集前沿具备更好的多样性特征，从而使最优解集在其中得到进一步的分散与丰富。具体优化时，其拥挤度主要按以下公式进行计算：

　　其中，id代表第i点位置的个体拥挤度；fji+1代表第i+1点位置上第j个目标函数的数值；fji−1代表第i-1点位置上第j个目标函数的数值。

　　3农机零部件加工中数控技术优化策略的实践应用分析

　　为判断上述优化策略在农机零部件数控加工技术中的应用效果，本次研究中，研究者特通过实验的方式对此项优化策略的实施情况进行分析。以下是具体实验设计、参数优化与优化效果分析情况。

　　3.1实验设计

　　本次基于NSGA-II算法的农机零部件数控加工技术优化策略实践应用中，研究者主要将农机零部件生产加工中最为典型的45#钢用作加工材料，对上述的数控技术优化策略应用进行实验。具体优化时，其加工参数的主要优化范围如下：（1）对于主轴转速n，其优化范围在2300～4300mm/r之间；（2）对于每齿进给量fz，其优化范围在0.05～0.3mm/r之间；（3）对于径向切削深度a e，其优化范围在2～4mm之间；（4）对于轴向切削深度a p，其优化范围在0.2～0.5mm之间。

　　3.2参数优化

　　在对本次实验中的农机零部件数控加工技术参数进行优化时，研究者主要借助于MATLAB-2018软件来建立NSGA-II算法框架，表1是本次实验中的NSGA-II算法基本参数设置情况。

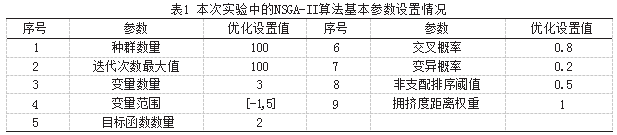
　　在NSGA-II算法运行之前，研究者先对Pareto解集前沿进行了求解，经求解可知，在通过上述措施对其数控技术进行优化之后，该农机零部件数控加工机床实际运行中的加工参数最优值如表2所示。

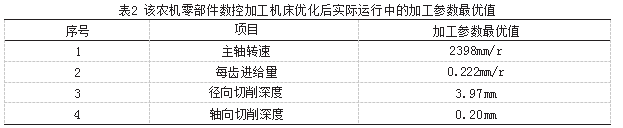
　　在通过上述方案对其进行优化之后，经进一步实践应用实验得出，该数控机床在正常加工农机零部件时的能耗是54.23kJ。

　　3.3优化效果

　　经上述的实践应用实验和相关研究发现，在通过NSGA-II算法对农机零部件数控加工技术参数进行合理优化之后，其数控机床在加工效率与加工精度上都实现了显著提升，同时也进一步降低了其正常加工条件下的运行能耗。经进一步研究可知，之所以会获得这样良好的优化效果，其主要原因是在对其数控机床的主轴转速、每齿进给量、径向切削深度以及轴向切削深度实施了合理优化，并获得了最优非支配解集之后，其加工效率、加工精度都可以得到良好改善[6]。同时，这样的最优加工参数组合也将会使数控机床运行能耗得到最大限度的降低，并有效降低刀具在加工过程中的损耗情况，使其使用寿命得以进一步延长。

　　由此可见，本次基于NSGA-II算法的农机零部件数控加工技术优化策略在农机数控机床加工中具有非常好的适用性与可行性，将其合理应用到此类数控技术的优化中，将会达到足够理想的优化效果，从而为现代农机零部件数控加工技术的优化、质量的提升及其能耗的降低提供有力支持，以此来促进此项数控技术的高效化、高质化、节能化与经济化发展。

　　4结语

　　农机零部件数控加工是当前机械加工领域中最为典型且常见的一项工作内容。而在此类机械的实际加工中，数控技术发挥着不可或缺的应用优势。为实现数控技术在其中的良好应用，进一步提升其加工效能与加工性能，研究者就需要对此类机床的优化策略进行深入研究，并结合实际情况，采取合理的优化算法对其进行优化处理。通过这样的方式，才可以进一步提升此类数控机床的加工效率及其加工精度，并达到良好的节能效果和经济效果，从而为此项技术及其生产加工领域的发展提供有力支持。

　　参考文献：

　　[1]武瑞梅.农业机械零件数控加工研究[J].南方农机,2024(08):153-155.

　　[2]邢献中.智能制造中数控加工和仿真技术研究[J].当代农机,2023(12):52-53.

　　[3]宋艳丽.数控系统对数控机床加工精度的影响因素探究[J].南方农机,2023(20):135-139.

　　[4]顾美.数控机床伺服控制技术体系与加工精度化途径[J].农机使用与维修,2023(10):53-55.

　　[5]张明.基于数控技术的智能插秧机结构参数优化研究[J].农机化研究,2023(10):76-80.

　　[6]孟晓华.农机轮盘零件的数控加工工艺分析[J].南方农机,2023(18):30-33.