摘要：轮胎是农用车辆行走系的重要部件，直接影响车辆各种使用性能的发挥。针对传统农用车轮胎在使用过程中易扎伤、易磨损等问题，设计了一种新型机械弹性车轮。利用有限元方法结合LMS模态试验，研究了各种因素对机械弹性车轮模态参数的影响机理和规律，计算了滚动状态下机械弹性车轮的模态参数，获得了转速对车轮模态参数的影响规律，从而得到了滚动状态下机械弹性车轮的模态特性。研究结果表明，机械弹性车轮在滚动状态下的模态特性可为其与农业车辆的匹配提供一定的指导。

　　关键词：机械弹性车轮；滚动状态；模态分析；农业车辆

　　我国作为农业大国，拥有20亿亩基本农田，每年需要大量农业机械辅助田间作业。根据***2018年12月份发布的《***关于加快推进农业机械化和农机装备产业转型升级的指导意见》，到2025年，全国农机总动力将达到11亿千瓦，市场发展前景广阔[1]，这也强有力地推动了相应农业车辆用轮胎的快速增长，近些年来，农业轮胎需求量的持续增长为中国轮胎产业平添了一个新的增量市场，其发展前景十分看好。轮胎是农用车辆行走的重要部件，其技术状况的好坏直接影响农用车辆的行驶性能和安全性[2]。农用车辆轮胎的故障主要是轮胎扎伤、磨损加快。轮胎扎伤主要是拖拉机等农业机械在坚硬农作物（如大豆、玉米、向日葵）秸秆地上作业时造成胎面扎伤；农用轮胎磨损加快主要是农用机械长期超负荷作业和超载，轮胎滑转率增加，加速了轮胎的磨损。若车辆两侧轮胎气压不同且相差较大，则气压低的轮胎磨损加剧[3]。

　　研究的机械弹性轮用机械耦合弹性复合结构取代了传统农用轮胎的空气弹性结构，在实现传统农用轮胎基本功能的同时具备机械弹性车轮具有的防爆、防弹和防刺破等优点[4]。所以弹性车轮更适合用于农用车辆。在前期研究的基础上[5-8]，针对所研究的机械弹性车轮模态特性，利用有限元方法结合LMS模态试验设备，研究了各种因素对模态参数的影响，并且计算了滚动状态下机械弹性车轮的固有频率和振型，获得转速对轮胎固有频率和振型的影响规律，即滚动状态下轮胎的模态特性。研究路线是首先进行车轮静态模态分析，研究车轮的结构参数对自由模态的作用效应。其次分析车轮在接地和承载不同载荷时的模态特性变化，以此探讨外界条件对车轮振动特性的调控作用。最后，研究车轮转速对模态特性的影响规律，以揭示转速变化对车轮振动行为的影响机理。研究中使用显式有限元分析，通过商业软件ABAQUS设置数值实验，模拟滚动轮胎实验中的变形规律。

　　1.机械弹性车轮结构

　　机械弹性车轮由鞣轮、轮毂和铰链组等部件装配而成，铰链组一端与鞣轮连接，另一端与轮毂连接。轮内部有多条弹性环，利用卡环将其固定后形成骨架，再用橡胶硫化成型，组成了鞣轮。机械弹性车轮结构如图1所示。

　　在工作状态时，铰链组由于受到车轴传给轮毂的垂直载荷与扭矩的作用，从平衡状态变成预紧状态，推动轮克服车轮与地面的摩擦力，使车轮滚动。轮毂悬挂于鞣轮内，当受到垂直载荷时，轮毂会向下移动，导致离地面较近的铰链组呈微弯曲状态，由于承受轮毂向下的拉力，轮在滚动时产生类椭圆变形[9]。机械弹性车轮能利用轮和铰链组的变形来吸收路面的激励，故其缓冲减震性能不同于普通的充气轮胎[10]。

　　2机械弹性车轮静态模态特性分析

　　2.1机械弹性车轮有限元模型

　　由于机械弹性车轮结构比较复杂，结合仿真时间及结果的收敛性考虑，对其进行简化处理。忽略轮胎花纹的影响、车轮主体对称、忽略弹性环和卡环之间的间隙等。基于上述简化思路，在CATIA软件建立车轮三维模型，并将其导入到ABAQUS软件中[11]。在ABAQUS中，鞣轮被定义为单个部件，并为鞣轮各分层区域赋予不同的材料参数[12]，采用连接单元模拟铰链组的连接结构，以确保铰链组的在仿真中的受力与实际加载过程中的受力相同。最终搭建的车轮结构有限元模型如图2所示。

　　2.2有限元模态计算

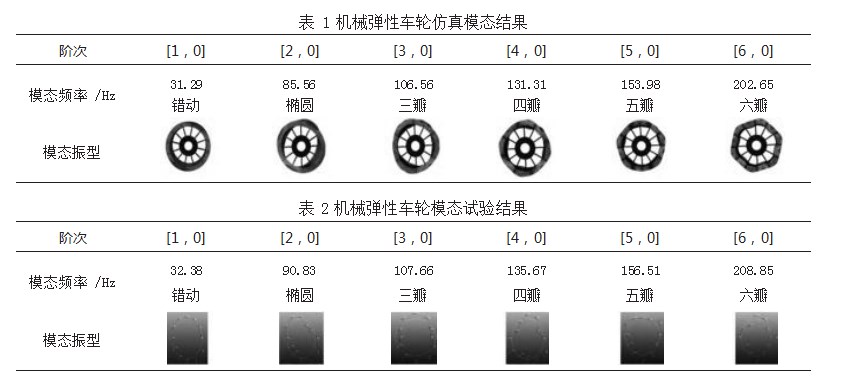
　　在ABAQUS软件中，根据实际情况定义机械弹性车轮的边界和加载情况，创建模态分析作业，定义求解控制选项（设置求解算法、收敛准则、迭代次数等），运行后可以获得模型的前6阶模态频率和振型（忽略刚体模态）。在此需要说明的是，为了方便和统一化，研究中采用参数表示法对振动模态或模态振型进行分类[13]，结果如表1所示。

　　2.3试验模态分析

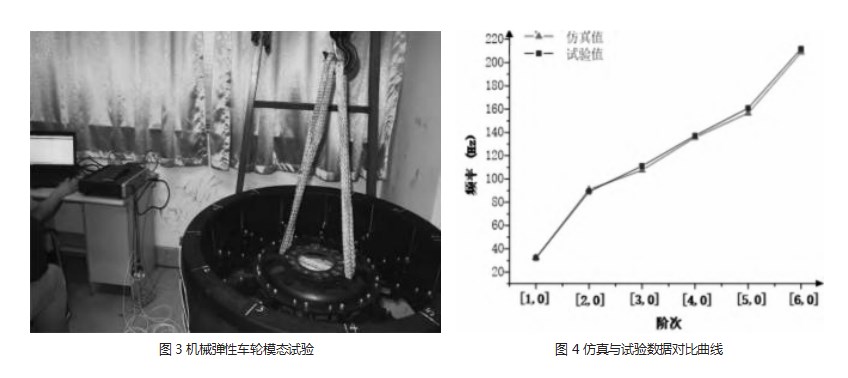
　　采用锤击法测量车轮的自由模态。将加速度传感器333B30固定在车轮的表面或内部，以记录振动数据。测试过程中，确保冲击力和位置尽量一致，以保证测试结果的可靠性。传感器的位置应该能够准确捕获轮胎的振动响应。设置测试参数，设置频带为512Hz和频率分辨率为0.83Hz。使用锤击器086C03轻轻敲击轮胎表面或侧面，产生一系列冲击，激发轮胎振动。利用多通道采集系统SCM205采集足够数量和质量的数据，利用模态实验分析系统LMS Test.Lab 13A对采集到的振动数据进行分析，包括振动频谱分析、模态识别等。通过分析振动模态，确定轮胎的固有振动频率和模态形态，以评估其结构和性能特性。

　　经检查弹性绳悬挂车轮对测试系统的弹性模态影响很小，故利用弹性绳将车轮自由悬置，进行自由模态试验，如图3所示。

　　2.4试验模态结果

　　在车轮模态测试中，由于车轮是对称结构，这类结构一般具有多组重根模态的特征，即会出现两个频率相同但完全独立的模态，而且可能会出现多组。实际中由于尺寸误差等因素，重根模态的频率可能不会完全相同，但一般都是比较接近，在频谱上是难以区分的。研究采用的是最小二乘复频域法，也称为Pol-yMax技术，该技术在抗干扰能力、识别耦合模态以及处理复杂结构方面具有非常好的特性，可以很好的识别重根模态。试验得出机械弹性车轮径向激振模态试验结果，如表2所示。

　　使用折线图将实验的模态频率和理论计算的模态频率绘制在同一图上（图4）。通过直观对比图形上的模拟值与试验值的数据变化趋势和分布，评估两者之间的一致性，误差较小。说明所建立的有限元模型具有较高的准确性，可用于进一步分析[14]。

　　3.机械弹性车轮静态模态影响因素

　　3.1载荷对车轮固有频率的影响

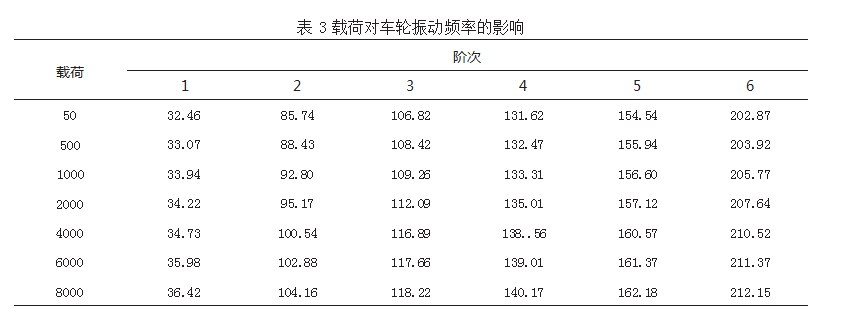
　　在车轮周向铰链组数量不变且车轮速度为零的情况下，分别对车轮施加50N、500N、1000N、2000N、4000N、6000N和8000N的载荷，计算车轮的固有振动频率。

　　获得车轮前6阶的固有频率，如表3所示。数据表明，除第二阶外，载荷对于车轮的振动频率影响不大，可以忽略。这是因为对于单一机械弹性车轮，在所施加的载荷范围内，其自身的结构不变，只是产生类椭圆变形，且刚度变化较小。

　　3.2材料弹性模量对车轮固有频率的影响

　　选取弹性环和橡胶外圈等效橡胶结构的弹性模量为输入值，可以获得弹性环和橡胶外圈两种材料弹性模量对车轮模态特性的影响规律，如表4所示。

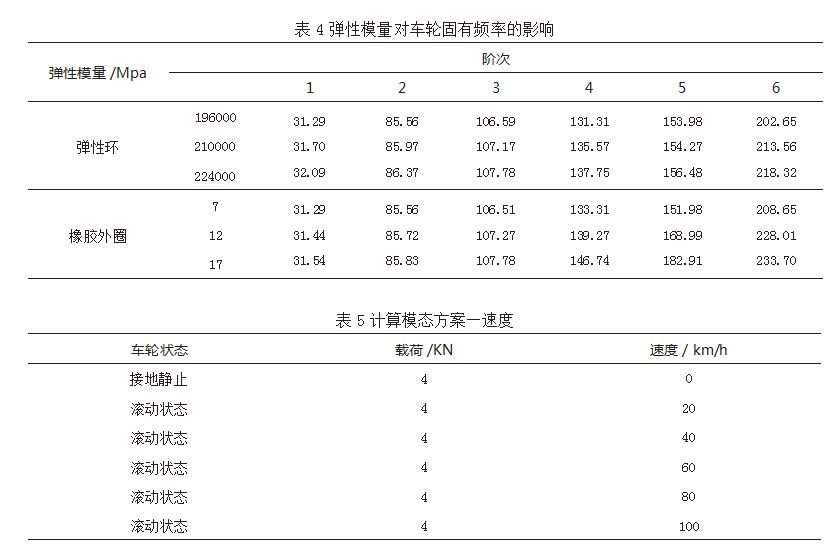
　　表4中的数据展现了同样一个规律，即随着弹性环和橡胶外圈结构的弹性模量的增加，车轮的每一阶固有频率都增大。但是增大的效果不明显，只有当材料的弹性模量增加幅度很大时，车轮的固有频率才会发生较大幅度的改变。

　　4机械弹性车轮滚动模态特性研究

　　4.1理论基础

　　4.1.1复模态理论

　　机械弹性车轮在稳定滚动过程中，受到预加载荷和体力的作用，而且与地面之间会产生摩擦力，另外车轮橡胶体结构和弹性环的迟滞变形决定着车轮的阻尼特性[15]，这些会对刚度矩阵和阻尼矩阵产生影响，导致非对称性，此时需要复模态理论。

　　模型的复特征值问题表述为：

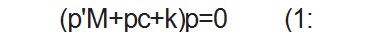
　　式中：M—系统质量矩阵;

　　K—系统刚度矩阵;

　　C—系统阻尼矩阵;

　　p—复特征值;

　　φ—复特征向量。

　　在软件ABAQUS/Standard中，使用子空间投影法提取复特征值。

　　4.1.2行波振动理论

　　在进行机械弹性车轮滚动状态下的模态分析时，需要考虑离心力、科氏力对固有频率的影响，以及由于转动而引起的行波振动[16]。当车辆轮胎滚动时，确实会产生一种行波。这种行波是一种机械波，它沿着轮胎滚动的方向传播，而且波的形状和特性在空间中保持不变。这种行波的产生是由于轮胎与地面之间的接触，当轮胎滚动时，地面对轮胎施加一个周期性的力，这种力的作用会导致轮胎表面形成一种波动，这种波动沿着轮胎滚动的方向传播，形成行波。行波的产生对于车辆的行驶和性能有一定的影响。例如，在高速行驶时，轮胎表面的行波会影响车辆的稳定性和行驶的平顺性。

　　行波可分解为沿正方向传播的前行波和沿负方向传播的后行波[17]。本文中与车轮滚动方向一致的振动波是前行波，反之亦然。

　　轮胎的有限元建模过程：通过命令，将轮胎的二维截面旋转生成一个壳体面，即三维轮胎有限元模型。此时将轮胎简化为一个壳体。下面介绍壳体或圆环的行波振动特点。

　　当考虑离心力时，转动壳体的固有频率与静止时略有差异。转动壳体固有频率为：

　　o,—静止时壳体的固有频率；BY—动频系数；

　　—转动壳体角速度；n—周向波数。

　　在静止坐标系中观测到的前、后行波频率为：

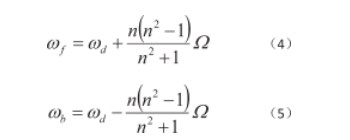
　　4.1.3离心力效应

　　离心力计算公式为：

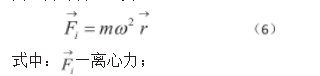
　　m—质点的质量；

　　—旋转速度；

　　r—转动半径，是矢量。加载离心力如图5所示。

　　4.1.4科氏力效应

　　科氏力来自物体运动所具有的惯性，但不是在惯性系中真实存在的力，而是惯性作用在非惯性系内的体现，它所在的非惯性系同物体一起转动[18]。

　　科氏力计算公式：

　　方程中有离心力和科氏力，根据公式（6）（7）这两个力都与轮胎的转速有关。运动方程求解得到的特征值（即固有频率）与轮胎转速相关。随着转速的增加，固有频率可能呈现出不同的变化趋势，通过深入分析固有频率与转速的关系，可以全面理解轮胎在不同工况下的振动行为，为轮胎设计和车辆性能优化提供科学依据。计算模态方案如表5所示。

　　由图7可知，机械弹性车轮在接地后固有频率会分裂成一大一小两个频率。根据行波振动理论，固有频率分裂的原因就是产生的前后行波的影响，前行波导致车轮固有频率增加，后行波导致固有频率下降。并且随着转速增加，前行波和后行波对固有频率的影响效应加剧，这解释了转速影响轮胎共振的机制。

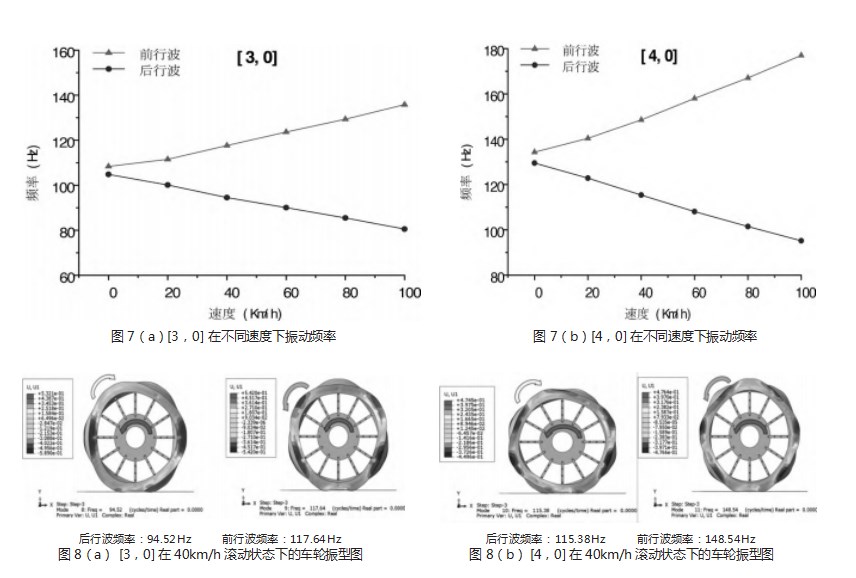
　　4.3转速对车轮模态振型的影响

　　图8是在40km/h滚动状态下车轮各阶次的振型图。红色箭头方向表示轮毂转向，黄色箭头是后行波方向，绿色箭头是前行波方向。

　　在机械弹性车轮旋转的过程中，整个车轮会产生两种不同频率的行波。前后行波频率是由系统本身的振动特性所决定，并可能相互独立被激发。当外界激振频率与前行波或者后行波的频率相同时，将引起共振，这使得滚动状态下机械弹性车轮的共振频率要增多，从而增加机械弹性车轮的共振概率[19]。

　　5.结论

　　（1）根据农业车辆在使用过程中轮胎易扎伤、易磨损的特点，提出了一种新型机械弹性车轮的设计，该设计更适用于农用车辆。

　　（2）以机械弹性车轮作为研究对象，建立了其有限元分析模型。通过LMS模态测试设备对该模型进行了静态模态计算，探讨了多种因素对轮胎模态参数的影响。

　　（3）车轮静态分析的结果对预测车轮动态特性作用有限。因而有必要研究滚动状态下的轮胎模态特性。研究结果为进一步研究机械弹性车轮的动态行为、滚动阻力、温度场分析和噪声分析提供了理论依据和技术支持，为其与农业车辆的匹配提供一定的指导。

参考文献:

　　[1]郝章程.农用子午胎:未来发展可期[J].中国橡胶,2021,37(10):7.

　　[2]宋涛.农用车行走系重要部件的使用与维护[J].农机使用与维修,2020,(06):85.

　　[3]汪泽.如何避免拖拉机"吃胎"[J].农业装备技术,2019,45(1):1.DOI:CNKI:SUN:JSNJ.0.2019-01-018.

　　[4]赵又群.非充气机械弹性安全车轮理论与方法[M].科学出版社,2020.

　　[5]Du X,Zhao Y,Lin F,et al.Numerical and experimental investigation on the camber performance of a non-pneumatic mechanical elastic wheel[J].Journal of the Brazilian Society of Mechanical Sciences&Engineering,2017,doi:10.1007/s40430-016-0702-8.

　　[6]Wang Q,Zhao Y,Du X,et al.Equivalent stiffness and dynamic response of new mechanical elastic wheel[J].Journal of Vibroengineering,2016,18(1):431-445.

　　[7]Zhao Youqun,Zang Liguo,Chen Yueqiao,et al.Non-pneumatic mechanical elastic wheel natural dynamic characteristics and influencing factors[J].Journal of Central South University,2015,22(5):1707-1715.

　　[8]Wang Qiang,Zhao Youqun,Lin Fen.Research on the Structural Transfer Path of New Mechanical Elastic Wheel Vibration,International Conference on Mechanics Design,Manufacturing and Automation(MDM2016),Suzhou,China,2016:743-753.

　　[9]王强,赵又群,杜现斌,等.机械弹性车轮径向刚度和阻尼模型的分析[J].中国机械工程,2016,27(10):1408-1413.

　　[10]汪伟,赵又群,姜成,等.新型机械弹性车轮的力学传递特性分析[J].江苏大学学报(自然科学版),2013,34(3):261-266.

　　[11]杜宜燕,赵又群.不同因素对机械弹性智能车轮加速度信号的影响[J].科学技术与工程,2022,22(10):4187-4195.

　　[12]朱跃,张令弥,郭勤涛.基于分层思想对复杂工程结构的有限元模型修正技术研究[J].振动与冲击,2011,30(12):175-180.

　　[13]Wheeler,Robert L,Dorfi H R,and Keum B B."Vibration Modes of Radial Tires:Measurement,Prediction,and Categorization Under Different Boundary and Operating Conditions[J].SAE Transactions,2005,114(6):2823-2837.

　　[14]Bai X R,Wang W F,Ge J M.New method of tire modal analysis with FEA[J].Tire Industry,2001,21(7):401-404.

　　[15]王强,赵又群,林,等.机械弹性车轮有限元计算与试验模态的相关性研究[J].哈尔滨工程大学学报,2017,38(1):86-93.

　　[16]Palanivelu S,Rao K V N,Ramarathnam K K.Determination of rolling tyre modal parameters using Finite Element techniques and Operational Modal Analysis[J].Mechanical Systems&Signal Processing,2015,64 65:385-402.

　　[17]Diaz C G,Kindt P,Middelberg J,et al.Dynamic behaviour of a rolling tyre:Experimental and numerical analyses[J].Journal of Sound&Vibration,2015,364(2):147-164.

　　[18]Matsubara M,Tsujiuchi N,Koizumi T,et al.Vibration Analysis of Tire Circumferential Mode Under Loaded Axle[J].SAE International Journal of Passenger Cars-Mechanical Systems,2013,6(2):1154-1160.

　　[19]周延泽,王春洁,陆震.高速滚动轴承保持架自由振动特性研究[J].北京航空航天大学学报,2001,27(5):596-599.