摘要：振动传感器采集的轴承故障信号极易被强噪声污染， 导致故障特征频率估计精度恶化。针对该问题， 提出一种基于自适应 噪声完备集合经验模态分解(CEEMDAN) 和双峭度准则的轴承故障特征频率高精度估计方法。使用 CEEMDAN 完成振动信号分解 之后， 从众多的备选模态中挑选出合适成分重构故障特征信号极具挑战。对信号分解获得的模态分量进行迷向圆变换(标准白化 处理) 后， 噪声对应的模态分量的分布更接近于正态分布。借助该信息， 引入双重峭度准则， 第一重峭度判定是在原始模态分量 中筛选出疑似的故障信号， 第二重峭度判定是借助迷向圆变换剔除掉噪声成分， 然后再使用这两重判定的交集模态完成对轴承故 障特征信号的重构。在此基础上，采用复包络法和 FFT 变换获取信号的包络谱， 然后使用三线谱校正法更为精准地估计轴承故障特征 频率。仿真实验和实测外圈、内圈故障数据表明， 与一些现有方法相比， 所提方法具有信号筛选方法简便、估计精度高等优势。

　　关键词： 自适应噪声完备集合经验模态分解; 轴承故障检测; 峭度;故障诊断

　　A Fault Characteristic Frequency Estimation Method of Motor Bearing Based on CEEMDAN and Double Kurtosis Criterion

　　Xie Chunwei1 ，Shen Weilin2 ，Yu Meiyi2

　　( 1. Guangzhou Electromechanical Technician College, Guangzhou 510435. China; 2. Foshan University, Foshan, Guangdong 528225. China) Abstract: Bearing fault signal collected by vibration sensor is easily polluted by strong noise, which degrades the accuracy of the fault characteristic frequency estimation. For this problem, a high accurate method of the bearing fault frequency estimation based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) and double kurtosis criterion is proposed. It is very challenging to select the appropriate components from alternative modes to reconstruct the fault characteristic signal after the signal decomposition. The distribution of the modal components corresponding to noise is closer to the normal distribution after the isotropic circle transformation (standard whitening treatment). Consequently, two kurtosis criterions are introduced. The first kurtosis criterion is to screen out suspected fault signals from the original modal components, and the second kurtosis criterion is to remove noise components by the isotropic circle transformation. Hence, the intersection modes of the double kurtosis criterion are used to reconstruct the bearing fault characteristic signal. Furthermore, the complex envelope method and FFT are used to obtain the envelope spectrum of the signal. In addition, the three-line spectrum correction method is employed to achieve more accurate fault characteristic frequency estimation. Compared with some existing methods, simulation experiments and measured bearing fault data of outer and inner rings show that the proposed method can obtain high accuracy estimates by a simple signal screening method.

　　Key words: complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN); bearing fault detection; kurtosis; fault diagnosis

　　引言

　　滚动轴承是一种常见的机械元件， 被广泛应用于电 动机， 是电动机中最容易发生故障的部件[1-2] ，及时发现 滚动轴承故障有助于提高整个系统的运维能力。研究滚 动轴承的运行状况，不仅可以促进故障诊断理论的发展， 而且也可以产生巨大的经济效益。当滚动轴承发生故障 时， 振动传感器所采集的信号中除了轴承故障所产生的 周期性冲击信号外， 还包含有大量背景噪声。因此， 如 何在背景噪声干扰下准确估计轴承故障特征频率是诊断轴承故障的关键。

　　由于可以将叠加着噪声的振动信号分解为一系列准 正交的子带信号， 从而能够有效抑制噪声干扰， 模态分 解类算法在滚动轴承故障特征分析中备受青睐[1-2]。文献 [3-4]已将经验模态分解(Empirical Mode Decomposition， EMD)算法应用于轴承故障特征频率分析中。但 EMD 算 法噪声稳健性差， 且经常出现模态混叠问题， 所以难以 满足实际应用的需求。通过在整个时频空间中填充高斯 白 噪 声 ， 集 成 经 验 模 态 分 解 (EEMD) 有 效 地 改 善 了EMD 的性能， 文献[5-8]将其应用于轴承故障特征频率提 取之中。但是残存在模态成分中的噪声， 将降低 EEMD 算 法 对 轴 承 故 障 特 征 频 率 提 取 的 准 确 性[9-10] 。相 比 于 EEMD， 自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise ，CEEMDAN) 有效降低了重构信号中的噪声残余， 因 而 有 着 更 好 的 模 态 分 解 性 能[9-11] 。 变 分 模 态 分 解 (Variational Mode Decomposition ，VMD) 改善了噪声稳健 性，现已广泛应用于轴承故障特征信号分析[12-16]。但在实 际使用中，VMD需要调节惩罚因子和模态个数等多个人工 参数，倘若惩罚因子或模态个数选择不当，模态混叠问题 依然存在， 因此难以满足形态各异的轴承故障诊断需求。

　　需要强调的是， 在使用模态分解算法对振动信号进 行分解后， 通常需要进行模态筛选， 以便于能够重构真 实的轴承故障特征信号。文献[3 ， 8 ， 11]指出， 轴承正 常运转时， 振动信号的幅值可用正态分布近似， 其峭度 值近似等于 3; 而一旦发生故障， 信号中大幅值振动出 现的概率增大， 信号会偏离正态分布， 峭度值也将随之 增大。因此， 可以用峭度来描述模态分量与故障特征信 号的关联性。但由于噪声干扰和模态混叠， 仅使用峭度 作为筛选准则时， 筛选出的模态中可能依然残存着强噪 声干扰[8]。为降低单独使用峭度带来的噪声残存风险， 文献[8]将自相关函数峰态系数和峭度准则相结合， 进行 模态分量的筛选， 有效消除了强噪声的影响。而文献 [17]则选择峭度值最大、包络熵最小的模态分量进行故 障特性信号重构。但当峭度最大值与包络熵最小值所对 应的模态不一致时，该方法将失效。

　　不同于上述两种准则相结合的方案， 本文仅以峭度 为故障特征信号的筛选准则， 但是需通过使用 2 次峭度 准则来实现故障特征信号的筛选。具体而言， 模态分解 之后， 用第一重峭度准则筛选出峭度值大于 3 的模态分 量， 记其索引值的集合为 I1.与此同时， 将模态分解结 果视作随机变量， 对其进行迷向圆变换[18] ， 即进行标准 白化处理， 在该变换之后， 噪声对应的模态分量的分布 近似于正态分布， 峭度值接近于 3. 这个信息可以用来 剔除噪声模态分量的影响。经过迷向圆变换后， 再使用 第二重峭度准则， 将各模态分量峭度值减去 3. 然后将 绝对值超过门限 ε 的索引值组成的集合记为 I2.选择双 重峭度准则获取的 2 个集合的交集， 即 I=I1∩I2 中的索引 值所对应的模态分量作为故障特征信号。仿真实验与公 开数据集测试证实了本文所提算法可以有效地提取轴承 故障特征频率。

　　1 处理流程与方法基本原理

　　如图 1 所示， 提出的轴承故障特征频率估计方法包 含 6 个部分： 去趋势处理、基于 CEEMDAN 的信号分解、迷向圆变换、基于双重峭度准则的信号筛选与重构、包 络提取与谱分析、谱峰位置校正。

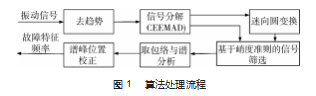
　　1.1 去趋势

　　因零点漂移， 振动传感器将出现趋势项。采用文献 [19]中的方法去除一阶趋势项。不失一般性， 将经过去 趋势的振动信号记为 x(t)。

　　1.2 CEEMDAN 算法原理

　　尽 管 通 过 加 入 成 对 正 负 高 斯 白 噪 声 ， EEMD 和 CEEMD 分解算法能够有效缓解 EMD 算法的模态混叠问 题， 但模态分量中残存的白噪声会对后续信号处理带来 负面影响。 CEEMDAN 使用 EMD 分解后含噪声的模态分 量替代高斯白噪声， 能够有效解决残存噪声问题。

　　将经过 EMD 分解得到的第 k 个模态分量记为 Ek(·)， wi 为高斯白噪声的第 i 次实现， σ 为高斯白噪声的标准 差。 CEEMDAN 算法的流程如下[20]。

　　( 1) 对于信号 x ( t) + σ0 wi ( t)， 得到其 I 次实现结果， 然后通过 EMD 获取第 1 个模态分量：

　　注意到 y(t) 的协方差矩阵为单位阵， 从而实现了从 s(t) 到 y(t) 的迷向圆变换。迷向圆变换本质上是对 s(t)进 行标准白化处理[18]。经过迷向圆变换之后， 噪声对应的 模态分量的分布更加近似于正态分布， 其峭度值近似等 于 3. 因此这个信息可以用来剔除噪声模态分量的影响。 1.4 双重峭度准则信号筛选

　　在正常工况下， 滚动轴承产生的振动信号， 其幅值 随时间的变化近似服从正态分布， 对应的峭度值约等于 3.随着故障的出现和演化，故障信号出现大幅值振动的 可能性增加， 其分布将偏离正态分布， 因而峭度值也随 之增大， 所以峭度常被用来筛选模态分量。然而在实际 应用中， 若仅单次使用峭度作为筛选准则， 则挑选出的 模态并不一定全是故障的特征信号。为此， 本文采用双 重峭度准则进一步剔除噪声的影响， 从而实现故障特征 信号的高精度重构，具体步骤如下。

　　1.5 包络提取与谱分析

　　采用文献[21]中的方法将重构信号 g(t)转化为复解析 信号 g°(t)，此时 g°(t) 的实部和虚部相互正交，g°(t) 的长 度为 g(t) 的 1/2. 即相当于进行了 1/2 下采样。然后对 | g°(t) |求快速傅里叶变换(FFT)， 即可得到其频谱图， 此处| ⋅ |表示取模操作。

　　1.6 谱峰位置校正

　　使用 FFT进行频谱分析时， 由于数据长度有限， 得 到的谱峰会有一定的展宽， 如果仅使用谱峰最大值进行 频率估计， 则并不能准确反映故障特征频率， 为此本文 采用文献[22]中的三谱线校正法。该方法需要两步来实 现， 第一步粗估计， 即挑选出 FFT 获取的频谱最大值所 对应的频率， 作为故障特征频率的初始估计值; 第二步 精细估计， 即基于最小均方根误差准则， 使用频谱最大 值及其前后各一个频谱值， 进行残差校正， 然后获得更 加精准的故障特征频率。

　　2 仿真实验

　　为验证所提算法对轴承故障特征频率估计的准确性， 通过仿真实验对其进行验证。轴承发生故障时， 由于滚 动体在故障处会产生冲击作用， 进而将形成周期性的振 动， 该振动信号会呈指数衰减。此外， 振动传感器采集 的信号中包含大量噪声， 因此仿真信号[23]可以表示为：

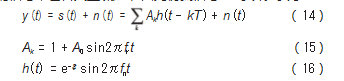
　　式中： s (t) 为周期性振动冲击信号; n (t) 为 0均值方差为 σ2 的高斯白噪声; A0 = 0.5 为幅度的初始值;fr = 30 Hz 为转轴的转动频率; ξ = 800 为衰减系数;fn = 3000 Hz 为共振频率;重复周期 T=0.008 s， 即故障频率为 125 Hz， 采样频率fs = 12 000 Hz，采样点数为 4 096.

　　图 2所示为信噪比为 0 dB情况下 50次蒙特卡洛实验 的包络谱平均值。为证实本文所提方法的有效性， 将它 与文献[8]中的方法进行对比。值得注意的是文献[8]采用 EEMD算法进行信号分解， 然后再使用自相关函数峰态 系数和峭度准则进行故障特征信号的筛选。由图可知， 在仿真条件下， 重构信号包络谱的峰算法值位置能够有 效反映出故障频率及其 2、3次谐波， 证实了本文所提算 法能够成功提取故障特征频率， 且在未校正之前， 所提 方法有着更低的基频、 2 次谐波误差。特别地， 本文方 法获得的故障特征频率平均值为 124.76 Hz， 文献[8]中方 法的平均值为 125.81 Hz。表 1 给出了经三谱线校正前后 故障信号特征频率的估计误差。表 1一方面说明校正对 估计精度的提升作用， 另一方面也说明了所提出算法的 误差更小。

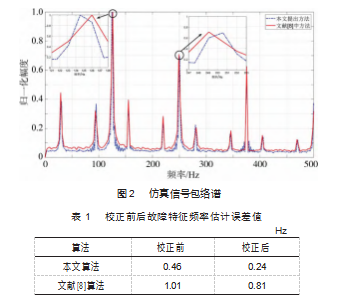
　　3 实测数据实验

　　为验证本文提出方法在实测轴承故障特征信号检测 中的有效性， 采用美国凯斯西储大学滚动轴承数据进行 验证分析。选取转速为 1 797 r/min、采样频率为 12 kHz 的数据， 电动机的转速频率为 29.95 Hz， 轴承型号为 JEM SKF 6205-2RS 深沟球轴承。

　　下面选用电动机驱动端加速度计数据对外圈故障、 内圈故障进行考察。需要指出的是， 在考察故障信号特 征频率估计准确性时， 为了保证公平性， 实验中文献[8] 中方法的结果亦经过了三谱线校正。

　　3.1 轴承外圈故障特征信号提取及其频率估计

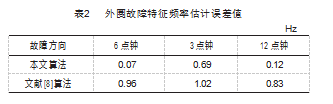
　　数据中轴承内圈完好无损，但外圈负载方向(6 、3、 12 点钟方向) 存在损伤， 损伤直径为 0.177 8 mm， 损伤 深度为 0.279 4 mm，选取 4 096个数据点进行分析， 轴承 外圈的故障频率为fo = 107.36 Hz。图 3~5 分别给出了 6、 3 、12 点钟方向外圈故障特征信号的包络谱。由图可知， 在外圈故障时， 采用本文方法能够准确地获取故障特征 信号的基频和高次谐波等。与文献[8]中方法相比， 本文 方法的高次谐波幅值更加明显， 更不容易被其他交互调 制信号干扰。

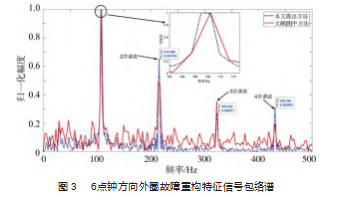
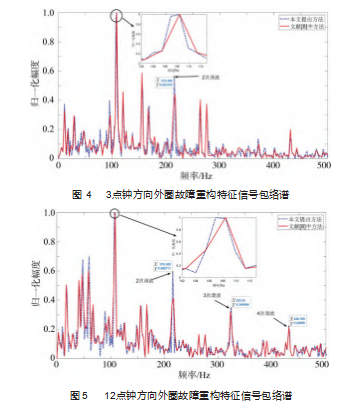
　　此外， 如图 3~5 中部分放大图所示， 因为数据长度 有限， 实际获取的故障特征信号谱线并非理想的单根谱 线， 而是具有一定程度的展宽， 直接选用峰值并不能准 确反映故障特征频率， 需要对其进行校正。如表 2 所示， 采用三谱线校正之后， 能够获得更为准确的故障特征频 率。特别地， 尽管实验中对文献[8]方法的结果也进行了 三谱线校正， 但是其估计误差依然远高于本文方法的误 差， 这再次说明了本文方法对外圈故障特征频率估计的 准确性。

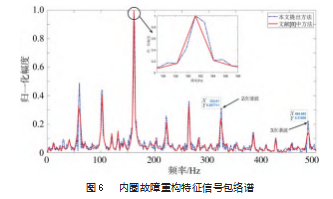
　　3.2 轴承内圈故障特征信号提取及其频率估计

　　该数据中轴承外圈完好无损， 但内圈有损伤， 损伤 直径为 0.177 8 mm， 深度为 0.279 4 mm， 选取 4 096 个数 据点进行分析， 轴承外圈的故障频率为fi = 162.19 Hz。 提出算法重构信号包络谱如图 6 所示。由图可知， 经 本文方法处理之后， 故障特征信号包络谱中故障特征 频率及其高次谐波非常明显。相应地， 本文方法与文 献 [8] 中 方 法 所 得 到 的 故 障 特 征 频 率 估 计 值 分 别 为 161.39 、 161.16 Hz。显然本文方法与理论故障特征频率 162.19 Hz 更为接近， 再次证实了本文算法能够有效提取 故障特征频率。

　　4 结束语

　　本文采用 CEEMDAN 算法对振动信号进行分解， 然 后使用双重峭度筛选准则对分解之后的信号进行筛选， 最终准确地重构了轴承故障特征信号。在此基础上， 采 用复包络法获取重构信号的包络谱， 最后再运用三谱线 法对包络谱的峰值位置进行校正， 获得了更为准确的故 障特征频率估计值。所提方法具有复杂度低、信号筛选 简便、估计精度高等优势。

　　为证实提出方法的有效性， 本文首先采用仿真实验 对轴承故障信号进行模拟， 验证了提出方法能够准确提 取故障特征频率及其高次谐波， 且准确度优于某些同类 型方法; 然后， 运用凯斯西储大学滚动轴承实测数据， 进一步验证当轴承内圈、外圈发生故障时， 本文方法能 够准确地提取故障的特征频率。

参考文献：

　　[1] RANDALL R B, ANTONI J. Rolling element bearing diagnostics —a tutorial[J]. Mechanical Systems and Signal Processing, 2011. 25(2): 485-520.

　　[2] 李军宁, 罗文广, 陈武阁 . 面向振动信号的滚动轴承故障诊断 算法综述[J]. 西安工业大学学报, 2022. 42(2): 105-122.

　　[3] 张超, 陈建军 . 基于 EMD 降噪和谱峭度的轴承故障诊断方法 [J]. 机械科学与技术, 2015. 34(2): 252-256.

　　[4] 苏文胜, 王奉涛, 张志新, 等 . EMD 降噪和谱峭度法在滚动轴 承早期故障诊断中的应用[J]. 振动与冲击, 2010. 29(3): 18-21.

　　[5] 王潇桐 . 基于 EEMD模糊熵和支持向量机的轴承故障诊断方 法[J]. 电气应用, 2021. 40(12): 14-19.

　　[6] 田晶, 王英杰, 王志, 等 . 基于 EEMD 与空域相关降噪的滚动 轴承故障诊断方法[J]. 仪器仪表学报, 2018. 39(7): 144-151.

　　[7] 王旭, 彭畅, 张振先 . 基于 EEMD 的共振解调技术在列车轴承 故障诊断中的应用[J]. 现代电子技术, 2015. 38(21): 24-27.

　　[8] 刘永强, 李翠省, 廖英英 . 基于 EEMD 和自相关函数峰态系数 的轴承故障诊断方法[J]. 振动与冲击, 2017. 36(2): 111-116.

　　[9] 周正南, 刘美, 吴斌鑫, 等 . 改进 CEEMDAN-小波包阈值降噪 在旋转机械轴承中的应用[J]. 自动化与仪器仪表, 2023(4):285-289.

　　[10] 刘敏, 叶艳媛, 杨清清, 等 . 基于 CEEMDAN 和倒频谱方法的 圆锥滚子轴承振动信号分析[J]. 机电工程技术, 2023. 52(8): 165-170.

　　[11] 李彦徵,栾孝驰,杨杰,等 .基于灰狼算法优化最大相关峭度反 卷积的滚动轴承振动特征提取与表征方法[J/OL].航空动力 学 报 : 1-18[2023-11-21]. https://doi. org/10.13224/j. cnki. jasp.20230338.

　　[12] 李波, 胡哿郗, 石剑钧, 等 . 基于多惩罚因子优化 VMD 的滚 动 轴 承 故 障 特 征 提 取 方 法 [J/OL]. 系 统 工 程 与 电 子 技 术 , 2023: 1-10. (2023-09-07). https://kns. cnki. net/kcms/detail/ 11.2422.TN.20230906.1954.018.html.

　　[13] 户文刚,张燕霞 .基于 VMD 和随机森林的离心泵滚动轴承故 障诊断[J].机电工程技术,2022.51(3):78-82.

　　[14] 王莹莹 ,陈志刚 ,王衍学 . 基于 WOA-VMD 联合 MOMEDA 的 轴承外圈故障特征提取方法[J/OL].机电工程:1-10[2023- 07-18]. http: //kns . cnki. net/kcms/detail/33.1088.th.20230714. 1733.002.html.

　　[15] 任学平, 李攀, 王朝阁 . 基于 VMD和MED 的滚动轴承微弱故 障特征提取[J]. 现代制造工程, 2018(3): 143-148.

　　[16] 杨秀宇, 邵斌, 贾少毅, 等 . 强背景噪声下滚动轴承轻微磨损 故障特征提取方法[J]. 煤炭工程, 2023. 55(5): 153-159.

　　[17] 邢芷恺, 刘永葆, 霍玉鑫, 等 . 基于 SVD 和 SSA-VMD 降噪的 轴承故障特征提取[J]. 热能动力工程, 2022. 37(9): 178-187.

　　[18] 张贤达 . 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004.

　　[19] 克莱尔 . 时间序列分析及应用: R语言[M]. 北京: 机械工业出 版社, 2001.

　　[20] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adap ‐ tive noise[C]//2011 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, 2011: 4144- 4147.

　　[21] MARPLE L. Computing the discrete-time "analytic" signal via FFT[J]. IEEE Transactions on Signal Processing, 1999. 47(9): 2600-2603.

　　[22] GIGLEUX B, VINCENT F, CHAUMETTE E. Generalized fre ‐ quency estimator with rational combination of three spectrum lines[J]. IET Radar, Sonar & Navigation, 2022. 16(7): 1107- 1115.

　　[23] 时培明,张慧超,伊思颖,等 .一种改进的自适应多元变分模态 分解轴承故障信号特征提取方法[J].计量学报,2022.43(10): 1326-1334.