摘要： 车辆隔振橡胶通常受到频率和振幅随时间变化的动态载荷作用， 需要建立不同应变比下橡胶疲劳寿命的高精度预测模型。 基于蜣螂优化算法(DBO) 和极限学习机(ELM )模型， 提出一种考虑不同应变比下隔振橡胶疲劳寿命的预测方法。基于隔振橡 胶试样单轴加载疲劳试验， 得到不同应变比载荷下试样疲劳寿命; 以应变幅值、应变均值与应变比为输入变量， 将橡胶疲劳寿命 作为输出变量， 利用 DBO 算法 优化ELM 模型中的输入层权值和隐含层偏置， 建立橡胶试样疲劳寿命预测 DBO-ELM模型。对比分 析所提出的 DBO-ELM模型、机器学习模型和幂函数模型下隔振橡胶预测寿命的精度。结果表明：基于 DBO-ELM模型的预测结果 与试验结果吻合最好， 能够显著提高橡胶疲劳寿命预测的精度， 验证了 DBO-ELM橡胶疲劳寿命预测模型的有效性。

　　关键词： 隔振橡胶; 应变比; 疲劳寿命预测;极限学习机;蜣螂算法

　　Fatigue Life Prediction for Vibration Isolation Rubber Components Based on DBO-ELM Model

　　Qin Wu1. 2 ，Li Chungui1 ，Pan Bingbing2 ，Li Jun1 ，HuJiantai2 ，Ge Pingzheng1. 3 ，Liu Feifei1

　　( 1.School of Mechatronics and Vehicle Engineering, East China Jiaotong University, Nanchang 330013. China; 2. Jianxin Zhao's Technology

　　Co., Ltd., Ningbo 315609. China; 3. Jiangxi Vocational and Technical College of Communications, Nanchang 330013. China)

　　Abstract: The vibration isolation rubber components of vehicle is excited by the alternate load. It is essential to establish the model for predicting the fatigue life under the different strain ratios. A prediction method for fatigue life is proposed based on dung beetle optimization (DBO) algorithm and extreme learning machine (ELM) model, considering the effect of strain ratios. With the uniaxially loaded fatigue test for rubber specimens, the fatigue life is obtained under different strain ratios; taking the stress amplitude, strain mean and strain ratio as the input variables, and the rubber fatigue life as the output variable, the DBO algorithm is used to optimize the input layer weights and implied layer bias in the ELM model to establish the DBO-ELM model for predicting the fatigue life of rubber samples. The accuracy of the proposed DBO- ELM model, machine learning model and power function model is compared. The results show that the prediction results under the DBO-ELM model have better consistency with experimental results; by using the DBO-ELM model, the prediction accuracy of rubber fatigue life can be significantly improved, which verify the effectiveness of the model for predicting rubber fatigue life.

　　Key words: isolation rubber; strain ratio; fatigue life prediction; extreme learning machine; dung beetle optimization

　　引言

　　天然橡胶因具有超弹性、黏弹性、能量吸收能力等 特性[1] ，被广泛应用于车辆减振领域。典型的橡胶隔振 元件包括动力总成悬置、橡胶衬套、联轴器和动力吸振 器等[2]。在连续交变载荷的激励下， 隔振元件容易发生 疲劳失效， 从而影响整车的操纵稳定性和安全性[3]。因 此， 准确地预测橡胶疲劳寿命， 能够确保橡胶隔振元件 在正常服役期间不发生疲劳失效。

　　目前， 隔振橡胶疲劳寿命预测模型和开展疲劳台架 试验是评估橡胶疲劳寿命的 2 种有效手段。其中台架疲 劳试验所需周期长且成本高，而橡胶疲劳寿命预测模型具 有高效且成本低的特点，受到了国内外学者的广泛关注。

　　传统的橡胶疲劳寿命预测模型的建立主要基于裂纹 萌生法[4]与裂纹扩展法[5]。裂纹萌生法是基于连续介质力 学方法， 通过建立损伤参量与疲劳寿命之间的幂函数关 系， 预测橡胶疲劳寿命。常用的疲劳损伤参量有最大主 应变[6]、等效应力[7] 和应变能密度[8]等。裂纹扩展法是基 于断裂力学方法， 通过构建裂纹扩展速率与撕裂能之间 的数学关系，预测橡胶的疲劳寿命。Yang 等[9]研究了扩展 点的分布和数量对裂纹扩展模拟结果的影响，基于应力强 度因子随裂纹深度呈指数变化的假设， 推导一种等效应 力强度因子幅值表达式， 可计算较大的裂纹扩展增量。

　　隔振橡胶的疲劳寿命与动态载荷息息相关。当动态 载荷激励隔振橡胶时， 橡胶会产生应变， 而应变特征(幅值、均值)会影响橡胶疲劳寿命。因此，需要考虑不 同应变比影响， 提高橡胶疲劳寿命预测的准确性[10]。

　　Pandey 等[11]基于连续介质损伤力学和扩展有限元的 方法， 建立了考虑应变比的损伤模型， 分析了不同应变 比下应变与疲劳寿命的关系， 得到了应变比对橡胶疲劳 寿命具有较大影响的结论。 Luo[12-13]基于橡胶材料剪切模 量和有效拉伸应变， 提出了预测疲劳损伤的方法， 得到 了不同应变比(包括正值与负值) 下的应变疲劳曲线。 上官文斌等[14] 分别以应变峰值和应变幅值为损伤参量， 建立不同应变比下的幂函数疲劳寿命预测模型， 研究结 果表明在正应变比和负应变比的加载下， 基于应变幅值 和应变峰值损伤参量的寿命预测模型可较好预测其疲劳 寿命。但橡胶疲劳失效过程具有随机性和长周期性特征， 传统橡胶疲劳寿命预测模型在假设限制、参数拟合、复 杂性因素和泛化能力等方面存在一定局限性。

　　近些年来， 机器学习算法已被成功应用于橡胶疲劳 寿命预测[15]。该方法是将影响橡胶疲劳寿命的关键参数 作为输入， 实测的橡胶疲劳寿命作为输出， 构建输入与 输出之间的非线性关系，从而预测橡胶疲劳寿命。相比于 传统的橡胶疲劳寿命预测模型，机器学习模型可以考虑数 据的随机性，其寿命预测精度较高。 Liu 等[16]研究了随机 森林机器学习算法，以应变均值、应变幅值和应变比作为 自变量， 建立了恒定振幅应力下橡胶疲劳寿命的预测模 型， 预测寿命结果聚集在 2 倍离散线以内。 Liu 等[17] 以应 变幅值和应变均值为输入变量， 橡胶疲劳寿命为输出变 量，建立支持向量机(SVM)模型，预测橡胶试样在恒幅 载荷下的疲劳寿命。 Wang 等[18]提出了一种基于支持向量 回归算法的橡胶预测寿命模型， 预测寿命结果聚集在 1.5 倍离散线以内。 Liu 等[19-20] 以峰值工程应变、环境温度和 材料邵氏硬度作为输入，将实测疲劳寿命作为输出，利用 ELM 模型与余弦算法优化的反向传播神经网络(BPNN) 模型， 预测寿命结果均分布在 1.5 倍离散线以内。

　　综上所述， 基于裂纹萌生法或裂纹拓展法通过不同 损伤参量建立的函数模型均为确定的数学表达式， 在诸 多方面存在一定局限性; 相比于裂纹萌生法或裂纹拓展 法， 因考虑了橡胶疲劳寿命的随机性， 机器学习算法预 测的橡胶疲劳寿命精度更高。但是， 目前基于机器学习 算法的隔振橡胶疲劳寿命预测的研究还存在以下问题： 机器学习模型中存在参数优化问题， 如 SVM 模型的惩罚 因子和核函数、 BPNN 模型的权重和偏置， 参数的选择 会极大影响模型的预测精度;对于橡胶疲劳寿命的预测， 已 经 有 多 种 机 器 学 习 算 法 被 应 用 ， 包 括 支 持 向 量 机 (SVM)、 反 向 传 播 神 经 网 络 (BPNN) 和 极 限 学 习 机 (ELM) 等。然而， 目前关于这些模型在橡胶疲劳寿命预 测方面的对比研究相对较少。

　　因此， 本文以哑铃状隔振橡胶试样为研究对象， 采 用位移控制法对橡胶试样进行单轴拉伸-压缩疲劳试验， 得到不同应变比加载下的位移 -应变曲线和疲劳寿命。 以应变幅值、应变均值和应变比为输入， 将实测橡胶疲 劳寿命作为输出， 研究基于 ELM 的橡胶疲劳寿命预测模 型; 根据 DBO 算法， 优化 ELM 模型中的输入层权重与隐 含层偏置， 构建 DBO-ELM 的疲劳寿命预测模型。以均 方误差和相关系数的平方(决定系数) 为模型精度评价 指标， 对比分析在 DBO-ELM 模型、 SVM 模型、 BPNN 模 型、 ELM 模型和幂函数模型下橡胶疲劳寿命的预测精 度。结果表明： 所提出的 DBO-ELM 模型在橡胶疲劳寿 命预测方面具有更高的预测精度， 训练集和测试集的疲 劳寿命预测值与实测值的均方误差和决定系数分别为 0.001 47 、0.019 39 和 0.994 56 、0.984 21. 预测寿命分布 在实测寿命的 1.5 倍离散线以内， 验证了基于 DBO-ELM 橡胶疲劳寿命预测模型的有效性。

　　1 隔振橡胶哑铃状试样疲劳试验

　　1.1 疲劳试验方法

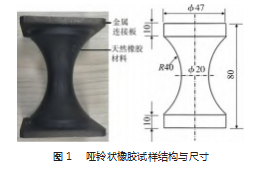
　　哑铃状试样具有结构简单、试验周期短、抗拉压载 荷能力强等优点， 被广泛应用于橡胶疲劳试验中。试样 通过金属连接板和天然橡胶材料在 150 ℃下硫化 7 min 而 成， 经打磨处理后的表面粗糙度为 1.2 µm， 结构与尺寸 如图 1 所示。

　　在实际载荷工况中，隔振元件主要承受拉伸和压缩载荷。图 2 所示为橡胶试柱疲劳试验机， 依据GB/T 1688—2008 标 准 中硫化橡胶伸张疲劳的测定， 进行哑铃状样件的单轴 拉 伸 - 压 缩 疲 劳 试 验 ，便于限定试验时对试样的疲劳载荷和位移控制。试验时 采用位移控制法将试样一端固定，在激励端加载轴向交变 位移载荷。采用六工位工装， 同时测试 6 个试样的疲劳寿 命。控制疲劳试验温度在(23±2)℃, 加载频率为 3 Hz。

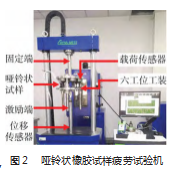
　　橡胶试样裂纹形成阶段的疲劳寿命占总寿命的90% 以上，疲劳寿命定义为试样完全断裂时的循坏次数，现将载 荷传感器和位移传感器的传递信号直接与计算机相连，实 时记录加载过程中载荷和位移的变化以及有效的计数次数。

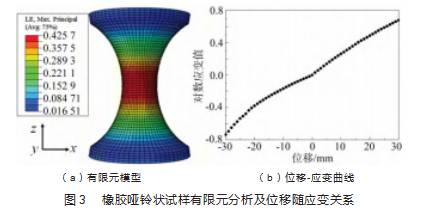
　　图 3(a)所示为哑铃状试样有限元分析模型， 采用 Mooney-Rivlin 模型作为本构模型描述橡胶材料的超弹性变形特性，其表达式为：

　　通过加载位移计算出应变(应变幅值、应变均值和 应变比)， 对试样进行有限元分析，模拟试样在疲劳试验 中相同的加载条件。分析时试样一端全约束， 一端加载 频率为 3 Hz 的正弦交变位移。选定轴向的对数应变分量 作为损伤参量， 以最大应变位置确定为疲劳损伤危险点。 试样危险点处的位移-应变曲线如图 3(b)所示。

　　1.2 不同应变比下的试验设计

　　由于裂纹闭合和应变结晶效应的存在， 应变比对橡 胶材料疲劳寿命有着显著影响。应变比定义为所施加的 激励载荷引起的橡胶试样的最小应变和最大应变的比值。

　　式中： R 为应变比; εmin 和 εmax 分别为最小和最大对数应 变值;εm 和 εa 分别为对数应变均值和幅值。

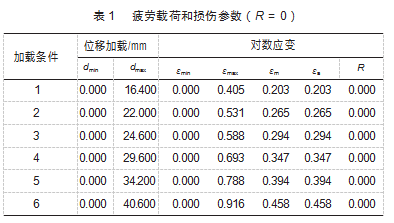
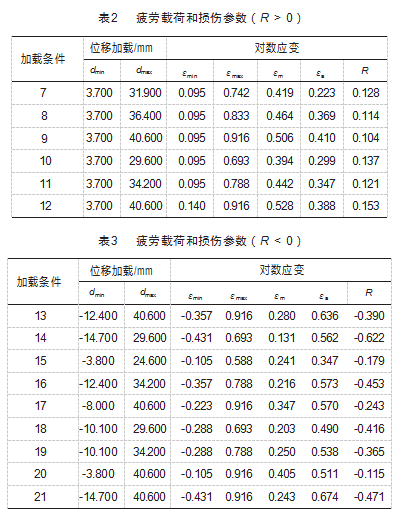
　　在哑铃状试样承载的交变载荷内， 根据图 3(b) 中 位移与应变关系，设计不同应变比(R = 0 、R > 0 和 R < 0)下 21 组试样疲劳试验，具体数据如表 1~3 所示。

　　研究表明， 橡胶在一定应变水平下的疲劳寿命服从 对数正态分布[21]。为避免数据离散性对结果的影响， 采 用式(3)将橡胶疲劳寿命的对数平均值作为实测寿命，其表达式为：

　　式中：N 为实测疲劳寿命;n 为同应变水平下橡胶疲劳寿命数据的个数; Ni 为第 i 次试验对应的橡胶疲劳寿命。

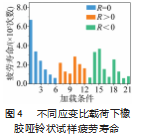
　　对上述加载条件进行疲劳试验， 对应的试样疲劳寿命如图 4 所示。

　　2 DBO-ELM 疲劳寿命预测模型建立

　　2.1 极限学习机模型

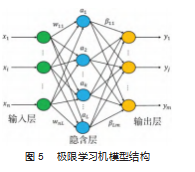
　　极限学习机是一种单隐含层前馈神经网络机器学习算法， 由输入层、隐含层和输出层共同组成的网 络 模 型[22] 。仅 设 定 隐含层神经元个数， 可在输出层获得全局最优解。以 n 个输入层神经元、 L个隐含层神经元、m 个输出层神经元组成的 ELM模型结构如图 5 所示。

　　式中： T为期望输出矩阵;H为隐含层输出矩阵;β为隐 含层与输出层之间的权重矩阵。

　　ELM模型的输入层权重 wi 与隐含层偏置 bj 随机产生 无需赋值，H为常数矩阵。因此，β 的求解可以视为求隐 含层和输出层之间权重的最小二乘解。根据广义逆理论，

　　2.2 蜣螂算法优化

　　蜣螂优化算法主要是受蜣螂的滚球、跳舞、繁殖、 觅食和偷窃行为的生物动机启发而提出的新型群智能优 化算法， 兼顾了全局探索和局部利用， 具有结构简单、 自适应性强、收敛速度快和求解精度高的优势[23]。构建 蜣螂优化算法具体步骤如下。

　　在蜣螂算法中， 负责滚球的蜣螂位置变化如下所示。

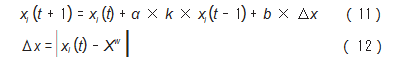
　　式中：t 为当前迭代次数;xi (t)为第 i 个蜣螂在第 t 次迭代 的位置信息; k ∈ (0.0.2) 为偏转系数; b ∈ (0. 1) 为随机 数; α 为-1 或 1的自然系数;X w 为全局最差位置; Δx 用 于模拟光强的变化。

　　当遇到障碍物时， 蜣螂会跳舞重新定位方向， 其位 置更新如下：

　　2.3 蜣螂算法下极限学习机模型中参数优化

　　ELM模型的期望输出矩阵取决于输入层权值和隐含 层偏置， 训练时参数随机生成需要多次调试。为使模型 获得最好的预测效果， 采用 DBO算法优化 ELM模型的输 入层权值和隐含层偏置， 构建基于 DBO-ELM 的橡胶疲 劳寿命预测模型，其流程如图 6所示。

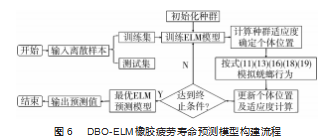
　　首先， 输入橡胶疲劳寿命原始样本数据， 随机划分 训练集和测试集， 初始化蜣螂种群并设定算法参数。其 次， 以模型预测值与样本实测值的均方误差作为适应度函数， 计算蜣螂种群自适应度并排序; 将适应度高的位 置 作 为 初 始 滚 球 位 置 ， 按 式 (11)( 13 )( 16 )( 18) ( 19)， 模拟蜣螂滚球、跳舞、繁殖、觅食和偷窃行为， 更新个体位置以及适应度; 当达到最大迭代次数时， 迭 代停止， 输出此时输入层权值和隐含层偏置。最后， 将 DBO 算法寻优得到的最优输入层权值和隐含层偏置赋予 ELM 模型，通过该模型进行橡胶疲劳寿命预测。

　　3 疲劳寿命预测结果分析

　　3.1 模型评价指标及其参数设置

　　通过衡量预测值与实测值之间的关系来评估判断模 型的预测效果， 采用均方误差 eMSE 和决定系数 R2作为模 型的评价指标。

　　均方误差值 eMSE 越小， 表明预测值与实测值越接近， 预测精度越高。决定系数 R2表示输出变量中能够被输入 变量正确预测的部分，R2越接近 1.模型拟合越准确。

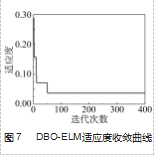
　　DBO-ELM 橡胶疲劳寿命预测模型及 DBO 优化算法 中的初始参数设定值如表 4 所示， 寻优过程中最优个体 适应度值的变化过程如图 7 所示。

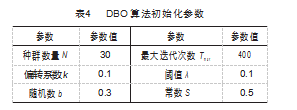
　　由适应度收敛曲线可知， 蜣螂优化算法在第 50 次迭代 时适应度值达到最低 ， 为 0.037.此时所搜寻到的输入 权值和隐含层偏置组合为最 优参数组合， 在之后的 350 次迭代中， 适应度值与最优 参数组合均未再发生变化。

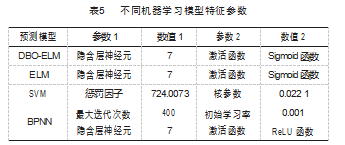
　　为了体现所提出的 DBO-ELM 模型的优势， 以应变 幅值、应变均值和应变比为输入， 选用 SVM[17] 、ELM[19]、 BPNN[20] 以及幂函数模型[14]分别对橡胶试样疲劳寿命进行 预测。

　　基于机器学习算法的预测模型均采用相同的训练集 和测试集， 通过多次试验、交叉验证和网格搜索[24]等方 法确定最优超参数组合， 不同机器学习模型特征参数设 置如表 5 所示。

　　对于幂函数模型， 分别以应变峰值和应变幅值为损 伤参量， 通过损伤参量与实测疲劳寿命之间的关系， 构 建常规橡胶疲劳寿命幂函数模型：

　　Nf = KSd ( 22)

　　式中：Nf 为橡胶疲劳寿命;K和 d为拟合试验数据得到的 材料常数; S 为疲劳损伤参数， 可选择应变能密度、应 力、应变等。

　　3.2 预测结果对比分析

　　为便于不同模型的分析对比， 采用标准归一化方法 对数据进行预处理， 避免某些特征对模型的影响过大。 为了更好地突出对比结果， 通过随机划分方法将数据集 随机地以 7 ∶ 3 的分配比例分成训练集和测试集。利用 100 组样本训练模型， 选择训练集中具有代表性的 15 个 样本分析。采用均方误差 eMSE 和决定系数 R2 评判模型性 能， 分析对比结果如表 6 所示， 不同机器学习模型训练 集和测试集的拟合结果分别如图 8 和图 9 所示。

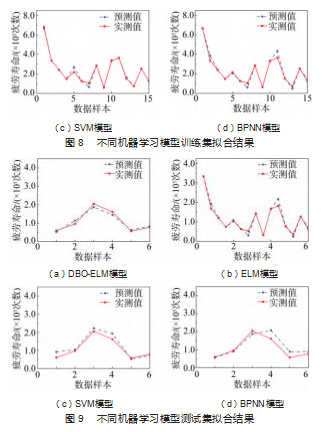
       由表 6 可知， DBO-ELM 模型训练集和测试集的 eMSE 分别为 0.001 47 和 0.019 39.相比于选用的其他预测模型 中表现最好的 ELM 模型， 训练集和测试集的 eMSE 分别下 降了 32.87% 与 42.05%; DBO-ELM 模型训练集和测试集 的 R2分别为 0.994 56 和 0.98 421. 相较于 ELM 、SVM 和 BPNN 模型， 其值更接近于 1.表明了所提出的模型具有 较好的拟合效果和较高的泛化能力。

　　由图 8~9 可知， DBO-ELM 模型训练集和测试集的疲 劳寿命的预测值与实测值误差波动较小， 变化趋势基本 一致。对比于无优化的 ELM 模型的预测结果， 其预测精 度提升较大， 同时相较于 SVM 模型与 BPNN 模型的预测 值， DBO-ELM 模型的预测效果也更好， 验证了 DBO- ELM 模型在橡胶疲劳寿命预测方面的优越性。

　　为了进一步评估模型的精度， 根据图 8~9. 不同机 器学习模型训练集和测试集的预测寿命分布图如图 10 所 示。由图可知， SVM 模型和 BPNN 模型训练集和测试集 的预测寿命均在 2 倍实测寿命离散线以内， 相比于 SVM 模型， BPNN 模型的寿命预测结果较离散， 可能是由于 试验样本数量少而导致模型陷入局部最优; DBO-ELM 模型和 ELM 模型训练集和测试集的预测寿命均在实测寿 命的 1.5 倍离散线以内， 且 DBO-ELM 模型的寿命预测结 果更接近于等寿命线。

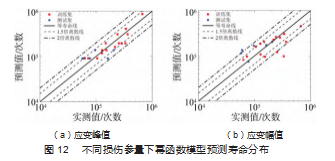
　　以应变峰值和应变幅值为损伤参量， 与橡胶疲劳寿 命拟合得到的幂函数模型表达式如式(23) ~( 24) 所 示，拟合曲线如图 11 所示。

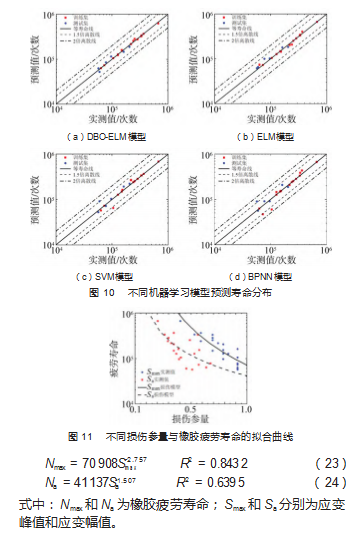
　　不同损伤参量下幂函数模型的预测寿命分布如图 12 所示。由图可知， 以应变峰值为损伤参量的预测寿命分 布在实测寿命的 2 倍分散线以内， 以应变幅值为损伤参 量的预测寿命分布在实测寿命的 2 倍分散线以外。由图 10 和图 11 可见， 与其他机器学习预测模型相比， DBO- ELM 模型在橡胶疲劳寿命预测结果更接近实测结果; 相 较于传统幂函数模型， DBO-ELM 模型能显著提高橡胶 疲劳寿命的预测精度。

　　4 结束语

　　( 1) 利用 DBO 算法优化 ELM 模型中的输入层权值 和隐含层偏置， 得到了优化后的参数， 确保了预测的疲 劳寿命均分布在实测寿命的 1.5 倍离散线以内， 提高了橡胶疲劳寿命的预测精度。

　　(2 ) DOB-ELM 模型的训练集和测试集的拟合效果 较好， 训练集和测试集的疲劳寿命预测值与实测值的均 方误差和决定系数分别为 0.001 47 、0.019 39 和 0.994 56、 0.984 21 ，验证了所提出的模型的有效性。

　　(3) 与 SVM 模 型 、ELM 模 型 和 BPNN 模 型 相 比 ， DBO-ELM 模型在橡胶疲劳寿命预测方面具有更好的预 测效果; 与幂函数模型相比， DBO-ELM 模型能显著提 高疲劳寿命预测精度， 体现出其在橡胶疲劳寿命预测上 的优越性。

参考文献：

　　[1] LIU X N, SHANGGUAN W B, ZHAO X Z. Probabilistic fatigue life prediction model of natural rubber components based on the expanded sample data[J]. International Journal of Fatigue, 2022. 163: 107034.

　　[2] 唐安特, 上官文斌, 潘孝勇, 等 . 橡胶隔振器高频动态特性的 计算方法[J]. 工程力学, 2020. 37(1): 230-238.

　　[3] YANG L, DAI X, ZHAO X, et al. Loading conditions impact on the compression fatigue behavior of filled styrene butadiene rub ‐ ber[J]. e-Polymers, 2023. 23(1):20228091.

　　[4] CHENG Z X, WANG H, WANG P. A multi-grid sampling multi- scale method for crack initiation and propagation[J]. Engineering Fracture Mechanics, 2022. 271: 108671.

　　[5] CHONG Z H, YUE T L, YAO Q L, et al. Experimental and nu ‐ merical investigation of crack propagation in bolting systems strengthened with resin-encapsulated rock bolts[J]. Engineering Failure Analysis, 2021. 122: 105259.

　　[6] 上官文斌, 段小成, 刘泰凯, 等 . 不同损伤参量对橡胶隔振器 疲劳寿命预测结果影响的研究[J]. 机械工程学报, 2016. 52 (2): 116-126.

　　[7] HOTTIN A, NAÏT ABDELAZIZ M, TALHA A, et al. Continuum damage mechanics to predict rubber fatigue life under multiaxial loadings[J]. International Journal of Fatigue, 2023. 170: 107559.

　　[8] PAN Z, LAI Y L, WANG Y P, et al. Fatigue life prediction and effects of cerium oxide-filled vulcanized natural rubber on fa ‐ tigue life under multiaxial loading[J]. Fatigue & Fracture of Engi ‐ neering Materials & Structures, 2021. 44(12): 3349-3362.

　　[9] YANG Y L, XU K B, CHEN H, et al. Research of optimization for crack propagation method[J]. Theoretical and Applied Frac ‐ ture Mechanics, 2022. 118: 103272.

　　[10] 吕向飞, 黄帅 . 考虑应变比影响的车用隔振橡胶疲劳寿命预 测方法[J]. 噪声与振动控制, 2021. 41(6): 211-214.

　　[11] PANDEY V B, SINGH I V, MISHRA B K. A Strain-based con ‐ tinuum damage model for low cycle fatigue under different strain ratios[J]. Engineering Fracture Mechanics, 2021. 242: 107479.

　　[12] LUO R K. Rubber fatigue prediction for filled natural rubber un ‐ der positive and negative R ratios[J]. International Journal of Fa tigue, 2022. 158: 106769.

　　[13] LUO R K. Shear modulus-based prediction of the fatigue life of antivibration rubber components[J]. International Journal of Fa ‐ tigue, 2022. 162: 107010.

　　[14] 上官文斌, 王小莉, 叶必军, 等 . 应变比对填充天然橡胶疲劳 特性影响的试验及其寿命预测方法研究[J].机械工程学报, 2013. 49(8): 49-56.

　　[15] 赵唯以, 陈沛涵 . 基于机器学习的单钢板混凝土组合板冲击 响应预测及优化[J]. 振动与冲击, 2023. 42(8): 28-37.

　　[16] LIU Q B, SHI W K, CHEN Z Y. Rubber fatigue life prediction using a random forest method and nonlinear cumulative fatigue damage model[J]. Journal of Applied Polymer Science, 2020. 137(14):48519.

　　[17] LIU X N, SHANGGUAN W B, ZHAO X Z. Residual fatigue life prediction of natural rubber components under variable ampli ‐ tude loads[J]. International Journal of Fatigue, 2022. 165: 107199.

　　[18] WANG X L, LIU J T. Intelligent prediction of fatigue life of nat ‐ ural rubber considering strain ratio effect[J]. Fatigue & Fracture of Engineering Materials & Structures, 2023. 46(5): 1687-1703.

　　[19] LIU X N, WANG X L. Natural rubber components fatigue life estimation through an extreme learning machine[J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2023. 237(1): 81-91.

　　[20] LIU X N, ZHAO X Z, SHANGGUAN W B. Fatigue life predic ‐ tion of natural rubber components using an artificial neural net ‐ work[J]. Fatigue & Fracture of Engineering Materials & Struc ‐ tures, 2022. 45(6): 1678-1689.

　　[21] LIU X N, ZHAO X Z, LIU X A. A unified probabilistic fatigue life prediction model for natural rubber components considering strain ratio effect[J]. Fatigue & Fracture of Engineering Materi ‐ als & Structures, 2023. 46(4): 1473-1487.

　　[22] ZHANG Z J, CAI Y M, GONG W Y. Semi-supervised learning with graph convolutional extreme learning machines[J]. Expert Systems with Applications, 2023. 213: 119164.

　　[23] XUE J K, SHEN B. Dung beetle optimizer: a new meta-heuris ‐ tic algorithm for global optimization[J]. The Journal of Super‐ computing, 2023. 79(7): 7305-7336.

　　[24] 李昕燃, 靳伍银 . 基于改进麻雀算法优化支持向量机的滚动 轴承故障诊断研究[J]. 振动与冲击, 2023. 42(6): 106-114.