摘要：采用有限元模拟方法对强风环境中的均压环结构的应力应变分布进行了深入研究，揭示了实际应用的均压环中的结构缺陷，同时采用控制变量法建立了两组对比模型，研究了均压环结构中的焊接接头连接形式和下支撑杆数量对均压环应力应变分布的影响，为均压环结构的进一步优化提供了方向。结果表明：均压环的下支撑杆与中环连接处应力集中最严重，是整个结构最易失效的部位；对于支撑杆与均压环的连接形式，锥形接口引起的应力集中程度最小，比当前使用的扁平接头更安全；当下支撑杆数量由3个增加到5个时，整体结构在强风下的最大应力值由39.0 MPa下降到26.4 MPa，最大位移量由2.11 mm下降到1.44 mm，都显著降低，表明此方法可以高效地缓解应力集中现象，同时还可以提高整个均压环结构的刚性。

　　关键词：均压环；有限元模拟；应力应变分析；铝合金

　　Abstract:The stress-strain distribution of the corona rings in strong wind environment is studied by using finite element simulation method,and the structural defects of the corona rings in practical application are revealed.Two sets of models are established for comparison by using the control variable method to study the influence of the welded joint connection form and the number of lower support rod on the stress-strain of the corona rings,which provides the direction for the optimization of the corona rings.The results show that the stress concentration at the connection between the lower support rod and the middle ring of the corona rings is the most serious,which is the most vulnerable part of the whole structure.However,the stress concentration caused by the conical joint is the smallest and safer than the present flat joint.When the number of lower support bars is increased from 3 to 5,the maximum stress values decreases from 39.0 MPa(3 bars)to 26.4 MPa(5 bars)and maximum displacements decreases from 2.11 mm(3 bars)to 1.44 mm(5 bars)in the overall structure,both are significantly reduced,indicating that this method can effectively alleviate the stress concentration phenomenon and also improve the rigidity of the entire corona rings.

　　Key words:corona rings;finite element simulation;stress-strain analysis;aluminum alloy

　　0引言

　　随着中国经济大跨越式发展以及各经济带建设的加快，我国的电力需求出现了快速增长，从而促进电力建设不断加强。由于我国各地区的能源储量分布不均，因此实现远距离、大容量的能源输送成为必然趋势，其中发展高压及特高压输电是主要策略[1-2]。然而，能源储量丰富的西北地区自然条件恶劣，在实际运行中电网系统仍存在高压电力设备稳定性较差、使用寿命短和检修困难等突出问题[3-4]。均压环是高压输电系统中必不可少的一个部分，它经常使用在输电线路和变电站中。均压环的基本工作原理是利用导体的电场分布效应将绝缘子以及开关周围较为集中的电场向外部扩展，使得周围电场的分布更加均匀，从而防止电晕、闪络等高压系统问题的发生，同时降低材料老化速率以及设备故障率。我国在110 kV及以上的高压输电线路上都会使用均压环，解决一些特殊部位电场过于集中的问题。然而，由于目前均压环的结构设计只考虑了对电场分布的影响，并未对均压环结构在服役环境中的稳定性及其应力分布进行分析，所以在均压环的实际服役过程中出现了大量由于强风、雷击冲击以及操作冲击引起的均压环开裂及失效情况，对电网系统的稳定性产生了恶劣影响。

　　目前，进行高压或超高压实验需满足的基础条件苛刻、破坏性实验多、同一条件下实验重复性差、对安全系数的要求高，所以国内外关于均压环特性的研究都采用先模拟后试验的研究思路，从而在减少现场试验次数的同时为试验提供有力的理论依据。有限元模拟方法[5-10]是目前均压环模拟的最常用方法，武汉大学首先建立了电场分布的数学模型，通过有限元方法计算了220 kV电压等级的复合绝缘子的电场分布情况，分析了不安装均压环及安装均压环2种情况下沿面电势和电场分布的情况，同时分析了均压环环径、管径和抬高距3个参数对电场分布改善效果的影响[11-13]，结果表明调节环径和抬高距对端部电场分布改善效果明显，其中调节管径对电场分布改善效果最优。司马文霞等人对超高[14-15]压输电线路合成绝缘子的均压环结构进行了全面分析，提出一种优化其结构参数的方法，该方法利用渐进边界条件解决静电场中边界开域问题，从而使用有限元的方法实现均压环结构优化的目标，最终目标是使绝缘子串周围各处电场都低于电晕起始场强。

　　目前，国内外对均压环的结构设计及安装规范都还没有统一标准，均压环的结构参数设置都是由各电力设计单位借助电场模拟和工程经验来完成的。然而，在当前均压环结构设计中只考虑了均压效果，并未深入研究均压环在工况下的结构稳定性。基于此，本文采用有限元模拟的方法，对国内已经投入使用的一种典型均压环结构进行模拟研究，通过分析其内部的应力应变分布情况来解析均压环在风压作用下的受力特点，并对现有结构的薄弱部位进行改进，研究结果能够为均压环结构的进一步优化提供参考。

　　1基于有限元的均压环模拟方法

　　有限元法是一种先进的数值计算方法，该方法只需要材料的本构模型、边界条件设置、施加约束等[16]即可模拟物体在实际工况下的应力应变等行为。采用该方法可以对复杂受力情况下的材料进行应力应变分析，并且分析的结果与实际情况比较符合，因而在工程应用中可以很好地指导和优化设计[17]。由于有限元法具有精度高、适应性强以及计算格式规范统一等优点，本文选择以有限元方法对在强风环境中服役的均压环结构进行模拟分析。

　　本文以抚顺电瓷的均压环为例，按实际尺寸建立了如图1所示的均压环模型，其中上环和中环由4个支撑杆连接，中环和下环由3个支撑杆连接，3个环的直径分别为0.95 m、0.95 m和2.15 m，均压环截面直径为150 mm，支撑杆截面直径为100 mm。整个均压环都由铝合金材料(A6061)制成，其中均压环和支撑杆的壁厚都为4 mm。另外，在有限元模拟过程中铝合金材料的密度、弹性模量、泊松比和屈服强度分别设置为2 700 g/cm3、7.1 GPa、0.33和60 MPa。为模拟我国西北地区的极端环境，以国标要求最大风速35 m/s(12级风)来计算作用在均压环上的风力载荷，将均压环工况模拟中的强风风速设置为35 m/s，模拟过程中暂不考虑风速的时变量，风压均匀地作用在均压环结构的迎风面上，同时根据实际的均压环安装方式将中间环内侧固定，并给整个均压环施加重力场。

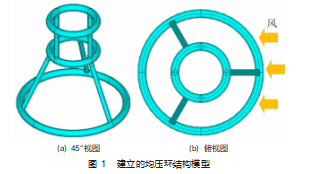
　　依据对我国新疆地区高压电网系统中均压环服役情况的调研可知，均压环与支撑杆的连接部位在实际服役条件下常出现开裂现象，如图2所示，但其失效原因尚不明确。本文通过模拟分析典型均压环在受风载荷下的应力应变分布特征来确定均压环在工况下的易失效部位，并初步对均压环结构进行优化，主要对比研究了均压环中的连接结构特征和支撑杆数量对其应力应变大小和分布的影响，为均压环结构的优化提供了方向和理论基础。

　　2结果与讨论

　　首先，以图1中建立的模型为例来分析风载荷作用下均压环结构的应力、应变分布和位移情况，其中均压环与支撑杆的连接形式采用更接近实际结构的扁平端口，如图3(a)所示。图3(b)是均压环的应力云图，可以看出支撑杆和均压环的连接处有明显的应力集中现象，其中下支撑杆和中环连接处的应力集中最严重，并且该处的应力值最大，为39 MPa。从局部放大图可以更清楚地看出，应力较大的区域大都集中在连接接口周围的中环上，与实际断裂位置相符。图3(c)是均压环在风载作用下的应变分布，由于整个均压环都采用同一种材质，所以该分布情况与应力分布非常接近。另外，在模拟条件下，模型中下环的位移量是最大的，其中最大位移量为2.11 mm，方向大致为Z轴正方向。在中环固定的情况下，对比上环和下环的位移量及应力应变分布情况可知，该均压环结构中下环与中环的连接是需要加强的，且下支撑杆与中环连接处是最易失效的部位，此模拟结果与工程实际中检测到的均压环断裂失效位置相符合，如图2所示。

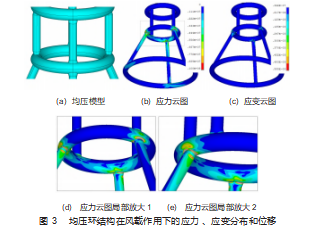
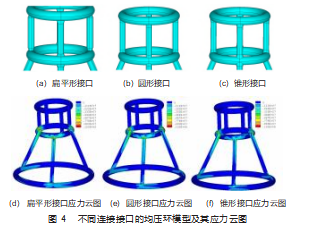
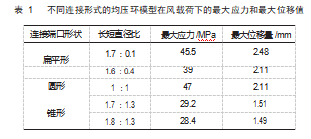
　　根据模拟结果和实际失效位置的考察，均压环与支撑杆连接处是最易失效的部位，强化支撑杆和圆环连接位置即可降低故障率。以往经验来看，强化连接处的方式有很多：从结构上看，可以直接增大连接处的壁厚、改变连接处形状、增加加强筋或增加不锈钢抱箍[18]等；从材料来看可以更换更高强度的材料[19]。由于均压环数量较多，考虑到施工难度以及成本，直接改变连接处形状是最为合理有效的方式，所以我们建立了具有不同连接形式的均压环结构，其连接接口主要分为扁平形、圆形和锥形3种：以支撑杆直径100 mm为一个单位长度，支撑杆与圆环中间平面相交处投影圆为基准做相互垂直的两条直径，扁平形接口的长短直径之比为1.7∶0.1，圆形接口即为1∶1，锥形接口为1.8∶1.3，如图4(a)~(c)所示，为了得出更为详细的数据变化趋势，增加了1.6∶0.4的扁平形接口和1.7∶1.3的锥形接口。图4(d)~(f)分别是具有不同连接方式的模型在风载下的应力应变分布情况，各个模型计算结果中的最大应力和最大位移量总结在了表1中。可以看出不同连接方式的均压环模型中整体的应力分布情况非常接近，同样都是下支撑杆和中环的连接处有严重的应力集中现象。对比最大应力值和最大位移量可知，扁平接口(1.7∶0.1)的最大应力值(45.5 MPa)和最大位移量(48 mm)均最大，同时扁平形和圆形接口的最大应力和最大位移量都明显大于锥形接口的相应值(28.4~29.2 MPa；1.49~1.51 mm)。同时从最值的变化来看，长短径的增大均会对应力集中情况有缓解，由于实际圆环尺寸的限制，直径不可能无限制的增大，需根据实际情况进行限制。综合分析以上模拟数据表明具有锥形端口的均压环的应力集中程度最小，是这3种结构中最好的连接形式。

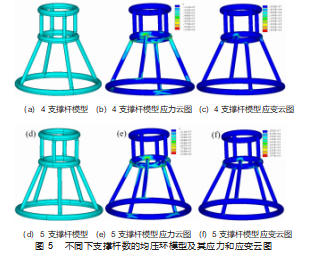
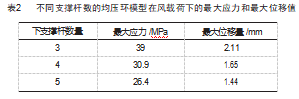
　　除了优化均压环结构的连接方式，实际工程中发现改变支撑杆数量也能够改变均压环结构的稳定性和寿命，所以我们也建立了具有不同下支撑杆数量的均压环结构并进行了模拟分析。图5所示是下支撑杆增加到4和5个的均压环模拟及其应力应变分布云图，3个下支撑杆模型的计算结果如图3所示。具有不同数量下支撑杆的均压环模型中的应力应变分布也是相近的，下支撑杆与中环的连接部位仍然是应力集中最严重的区域，也是最大应力值出现的位置，表明增加支撑杆后该处仍然是易失效部位。表2中总结了具有不同支撑杆数的均压环在风载作用下的最大应力值和最大位移量，从模拟数据来看，原本中下3支撑杆模型最大应力为39 MPa，更改为4支撑杆后，模型最大应力减小到了30.9 MPa，5支撑杆模型最大应力仅为26.6 MPa，可以明显看出随着均压环中下支撑杆数量的增加最大应力值有了明显的减少，同时最大位移量也从2.11 mm减小到了1.44 mm，表明下支撑杆数量的增加有效缓解了应力集中现象，同时还提高整个均压环结构的刚性，所以增加下支撑杆数量是一种提高均压环稳定性的有效途径。

　　结合仿真分析结果和实际发生断裂的情况可以看出，运行在大风环境中的均压环结构设计至关重要，针对高风载地区的均压环可采取减少应力集中的方式来优化均压环结构，从而大幅提升均压环长时间服役的可靠性。

　　3结束语

　　本文采用有限元模拟典型均压环结构，分析其内部应力、应变分布并解析其在风压作用下的受力特点，定位薄弱环节，提出均压环结构的优化方式，结论如下。

　　(1)在典型均压环结构中下环与中环之间的连接需要加强，且下支撑杆与中环连接处应力集中最严重，是均压环最易失效的部位。

　　(2)相比于扁平接口(实际均压环结构中的连接形式)和圆形接口，锥形接口引起的应力集中程度更小，是一种更好的支撑杆与均压环的连接形式。

　　(3)当均压环结构中的下支撑杆数量由3个增加到5个时，整体结构中的最大应力值从39.0 MPa降低到了26.4 MPa，同时最大变形量也从2.11 mm降低到了1.44 mm，表明增加下支撑杆可以有效地缓解应力集中现象，同时还可以提高整个均压环结构的刚性，是一种提高均压环安全性和稳定性的有效途径。

　参考文献：

　　[1]蒋伟,黄震,吴广宁.特高压输电系统绝缘问题的综述[J].现代电力,2007,24(4):10-16.

　　[2]ANNESTRAND S A.Ultra high voltage transmission technology report on Italy/USA joint UHV workshop[J].Power Engineering Review,IEEE,1982,PER-2(10):10-12.

　　[3]方欣.复合绝缘子电场分布计算及均压环参数设计研究[D].长沙:湖南大学,2015.

　　[4]刘春雨.均压环与球电极风沙侵蚀及表面特征的起晕电压研究[D].保定:华北电力大学,2020.

　　[5]王丽君,刘卓.特高压干式空心电抗器电场仿真及均压装置设计[J].电力电容器与无功补偿,2015,36(2):56-60.

　　[6]王加龙,彭宗仁,刘鹏,等.±1 100 kV特高压换流站阀厅均压屏蔽金具表面电场分析[J].高电压技术,2015,41(11):3728-3736.

　　[7]ABDERRAZZAQ M H,JALGIF A.Characterizing of coronarings applied to composite insulators[J].Electric Power Systems Research,2013,95:121-127.

　　[8]DIAZ-ACEVEDO J A,ESCOBAR A,GRISALES-NOREA L F.Optimization of corona ring for 230 kV polymeric insulator based on finite element method and PSO algorithm[J].Electric Power Systems Research,2021,201:107521.

　　[9]周锋.均压环对覆冰特高压直流复合绝缘子电场分布的影响[J].电气技术,2011(12):24-27.

　　[10]牟向伟.机械专业有限元法课程几个关键问题的思考与探索[J].广西物理,2014,35(2):45-47.

　　[11]李自品,段开洪,刘生琳.基于子模型法的330 kV线路绝缘了串电压分布计算[J].武汉大学学报(工学版),2006,39(1):92-96.

　　[12]吴光亚,王钢,蔡炜,等.±500 kV直流复合绝缘子的电位分布特性.高电压技术,2006,32(9):132-135.

　　[13]樊亚东,文习山,李晓萍,等.复合绝缘子和玻璃绝缘子电位分布的数值仿真[J].高电压技术,2005,31(12):1-3.

　　[14]司马文霞,杨庆,孙才新,等.基于有限元和神经网络方法对超高压合成绝缘子均压环结构优化的研究[J].中国电机工程学报,2005,25(17):115-120.

　　[15]司马文霞,武坤,李立浧,等.±800 kV线路直流复合绝缘子均压环结构研究[J].高电压技术,2007:33-36.

　　[16]梅志恒,刘淑杰,邓威威.基于ANSYS的航空发动机涡轮叶片有限元仿真[J].机电工程技术,2021,50(11):33-36.

　　[17]高兴军,赵恒华.大型通用有限元分析软件ANSYS简介[J].辽宁石油化工大学学报,2004,24(3):94-98.

　　[18]秦睿,高健,严丽,等.一起均压环断裂故障的分析与处理[J]高压电器,2014,50(7):117-122.

　　[19]黄水平,谭志聪,许家政.一起500 kV母线保护动作跳闸分析[J].装备制造技术,2014(5):246-247.