摘要：基于交流绕组理论，推导了逆变器供电下永磁同步电主轴的气隙磁密表达式，指出逆变器供电时存在特定的谐波电流，该电流会产生特定的气隙磁密。通过建立电磁场数值计算模型，分别施加正弦波供电和逆变器供电条件进行验证，得到在不同的供电条件下气隙磁密的分布状态，验证了理论推导。同时推导了逆变器供电下永磁同步电主轴的径向电磁力表达式，总结了径向电磁力的来源和时空分布特征，指出逆变器供电产生了特定空间阶次和时间阶数的电磁力，又采用电磁场数值方法计算了永磁同步电主轴的径向电磁力并对其进行了2D-FFT分解，直观展示了正弦波供电和逆变器供电下径向电磁力的显著差异，再次验证了理论推导的正确性。最后结合电机的结构原理，指出在实际中应尽量避免和消除能够产生低阶次电磁力。

　　关键词：永磁同步电主轴；逆变器供电；气隙磁密；径向电磁力；2D-FFT分解

　　Abstract:Based on the theory of AC winding,the expression of air-gap magnetic density of permanent magnet synchronous spindle under inverter power supply is derived.It is pointed out that there is a specific harmonic current when power supply is from inverter,which will produce a specific air-gap magnetic density.By establishing electromagnetic field numerical calculation model,the distribution of air-gap magnetic density under different power supply conditions is verified by applying sine wave power supply and inverter power supply conditions respectively,and the theoretical derivation is verified.The expression of radial electromagnetic force of permanent magnet synchronous spindle under inverter power supply is also deduced,the source and space-time distribution characteristics of radial electromagnetic force are summarized.It is pointed out that the inverter power supply generated a specific spatial and temporal order of electromagnetic force.Then the radial electromagnetic force of permanent magnet synchronous spindle is calculated using electromagnetic field numerical method,and 2D-FFT decomposition of the force is carried out.The results show the significant difference of the radial electromagnetic force under sine wave power supply and inverter power supply,and again verifies the correctness of the theoretical derivation.Finally,combined with the structure principle of the motor,it is pointed out that the low order electromagnetic force should be avoided and eliminated as much as possible in practice.

　　Key words:permanent magnet synchronous spindle;inverter power supply;air gap magnetic density;radial-electromagnetic force;2D-FFT decomposition

　　0引言

　　在数控机床领域，电主轴取代机械主轴的趋势愈发显著[1]。永磁同步电主轴因其效率高，响应快，低速运转性能佳等特点，其应用范围不断扩大[2]。振动是评价主轴性能优劣的重要指标，其驱动电机的噪声和振动是评价电机质量的重要指标之一[3]。过高的振动不仅会影响电主轴的加工精度，而且还会降低电主轴的寿命，引发噪声，造成环境污染。

　　驱动电机的振动主要由径向电磁力波引起，近年来国内对电机振动研究有了一定的研究成果。文献[4-5]使用解析法和有限元法对分数槽直流无刷永磁电机的径向电磁力进行了研究，指出定子槽开口对电枢反应磁场的影响较小。文献[6-8]对表贴式永磁电机进行了研究，提出了通过磁极偏心、开辅助槽、优化选择极弧系数等方法来降低空载电磁力。文献[9]提出了一种对分数槽永磁同步电机的气隙磁密波形进行重构的思想，为低振动、低噪声电机的研发开拓了一种新的思路。此外还有一些通过驱动控制的方向来降低电机振动的方法[10]。然而，目前针对永磁同步电机的电磁振动及径向电磁力的研究大多集中在理想正弦波供电的条件之下[11-12]，实际上以永磁同步电主轴为代表的调速永磁同步电机几乎都采用了逆变器供电的方式，这种形式下电流波形并不是理想的正弦波，而是存在大量的谐波[13]，谐波电流的存在必将极大丰富电机的径向电磁力分布，进而产生额外的电磁振动和噪声，甚至还会引起结构共振，严重影响电主轴的可靠运行，因此有必要继续进行深入的研究。

　　1逆变器供电对永磁同步电主轴气隙磁场的影响

　　1.1解析分析

　　当忽略铁心饱和影响时，永磁同步电主轴的气隙磁密表达式为[14]：

　　b(θ,t)=f(θ,t)λ(θ,t)(1)

　　式中：f(θ,t)为气隙磁势；λ(θ,t)为气隙比磁导。

　　从式(1)中能看出，电机的气隙磁密为气隙磁势与气隙比磁导的乘积。根据电机学原理，正弦波供电时，电机的气隙磁势包括定子基波磁势、定子谐波磁势和转子谐波磁势，即

　　f(θ,t)=f0(θ,t)+ν(θ,t)+μ(θ,t)(2)

　　当永磁同步电主轴采用逆变器供电与采用正弦波供电相比时，其定子谐波磁动势将分为基波电流产生的定子谐波磁动势和l次时间谐波电流产生的定子谐波磁动势。4种磁势分别如式(3)~(6)所示。

　　定子基波磁动势：

　　式中：p为极对数；ν为定子电枢谐波；l为逆变器谐波

　　电流；μ为转子谐波；θ为空间角度；ω0为电角速度；

　　φ0,1,2,…为相位角。

　　根据文献[3]，定子开槽时的气隙比磁导可近似表示为：

　　1.2电磁场数值分析

　　以一台4极36槽内嵌式永磁同步电主轴电机为例，其电机截面如图1所示，其基本参数如表1所示。

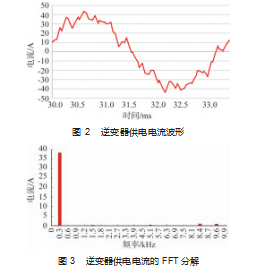
　　利用电磁场数值分析方法，设置3 kHz载波频率的逆变器供电条件，其电流波形如图2所示，显然富含谐波电流。对其进行FFT分解，如图3所示，可见除了300 Hz的基波电流外，在8 400 Hz和9 600 Hz处的谐波电流幅值较高，进一步分析可知逆变器供电时谐波电流的分布规律如式(9)所示：

          fl  = k 1 fT   ± 2k2 f0                                                                                                      ( 9 )

　　式中：fl为谐波电流频率，Hz；fT为载波频率，Hz；f0为基波频率，Hz；k 1,k2=1，2，3，…。

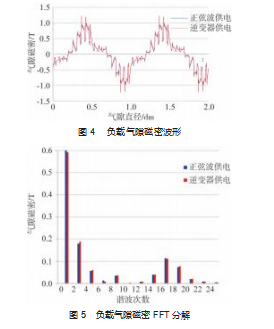
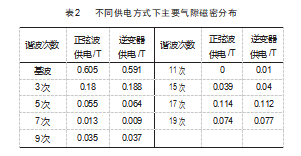
　　分别施加正弦波供电和逆变器供电，得到额定负载的气隙磁场波形，由于时间谐波电流影响了电枢反应磁场，导致正弦波供电和逆变器供点的气隙磁场存在差异，如图4所示。对图4的气隙磁场波形进行FFT分解，其结果如图5所示。从图5中能看出，相比正弦波供电，逆变器供电下电机的基波气隙磁密略有降低，3次、5次、11次等较低阶次的谐波磁密均有不同程度的增加，其中11次谐波从0特斯拉(T)增加到0.01特斯拉(T)，详见表2。可见逆变器供电改变了气隙磁场的分布状态，异常气隙磁密的产生必将造成电机运行状态的改变。

　　2逆变器供电对永磁同步电主轴电磁力的影响

　　2.1解析分析

　　根据Maxwell应力方程，旋转电机的径向电磁力可表示为：

　　式中：br(θ,t)为径向气隙磁密，T；pr(θ,t)为径向电磁力，N/m2。

　　将式(8)代入式(10)，并经整理后得到径向电磁力的展开式(11)：

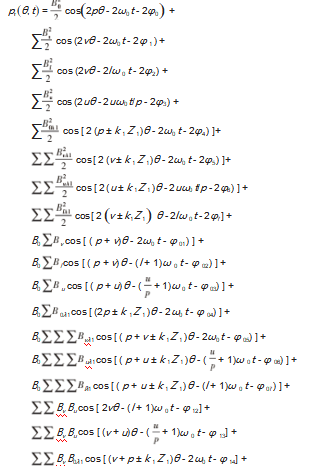
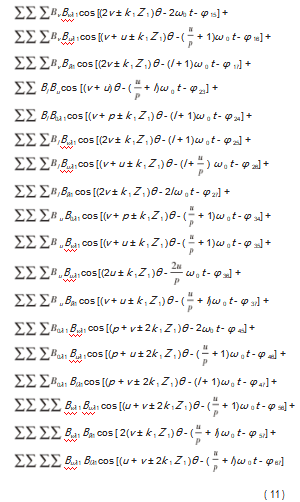
　　通过式(11)可以得出逆变器供电时径向电磁力的产生来源，将径向电磁力的空间阶次和时间阶数汇总成表3。由于永磁体是气隙磁场的最主要来源，因此逆变器供电而产生的电磁力主要由其谐波电流的电枢反应磁场和转子永磁体磁场相互作用，其空间特征为0和±2k 1p，时间特征为k 1 fT±k2 f0。

　　2.2电磁场数值分析

　　应用电磁场数值分析方法对式(10)进行求解，并对所得径向电磁力进行2D-FFT分析，分别得到正弦波供电和逆变器供电条件下的径向电磁力时空分解图，如图6~7所示。

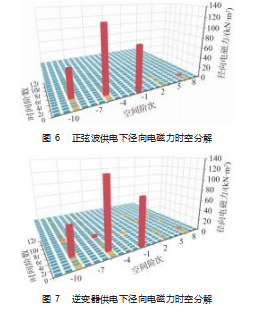
　　器供电下永磁同步电主轴的径向电磁力的分布趋于复杂，详见表4。

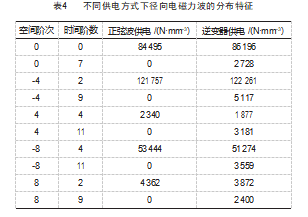
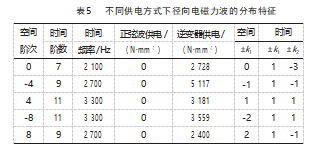
　　从表4能看出，逆变器供电时新增了0阶7倍频、-4阶9倍频、4阶11倍频、-8阶11倍频、8阶9倍频等不同空间阶次、不同时间阶数的径向电磁力。结合载波频率fT为3 000 Hz，基波频率f0为300 Hz的电机基本参数，分析可知新增的电磁力分布完全符合2.1节空间阶次0，±2k 1p，时间阶数k 1 fT±k2 f0的结论，证明了理论分析的正确性，如表5所示由于定子铁心的变形量约于电磁力空间阶数的4次方成反比，与力波幅值成正比[15]，径向电磁力波的次数越低，铁心弯曲变形就越大，因此，在实际中应尽量避免和消除能够产生低阶次电磁力的谐波。

　　3结束语

　　本文以一台4极36槽内嵌式永磁同步电主轴为研究载体，通过理论推导和电磁场数值分析，证明了理想正弦波供电和逆变器供电的方式存在显著区别。首先，逆变器供电存在分布特征为k 1 fT±2k2 f0的谐波电流，该电流将产生分布特征为l cos(νθ-lω0 t-φ2)和Blλ1 cos[(ν±k 1 Z 1)θ-lω0 t-φ7]的气隙磁场；其次，该谐波电流的电枢反应磁场和转子永磁体磁场相互作用，产生了空间特征为0和±2k 1p，时间特征为k 1 fT±k2 f0的径向电磁力，进而产生额外的电磁振动和噪声，甚至还会引起结构共振，现实中绝不可忽视。

参考文献：

　　[1]陈仕彬.滑动轴承支撑机电耦联轴系的稳定性分析[D].沈阳:沈阳工业大学,2012.

　　[2]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.

　　[3]陈永校,诸自强,应善成.电动机噪声的分析与控制[M].杭州:浙江大学出版社,1987.

　　[4]ZHU Z Q,XIA Z P,WU L J,et al.Analytical Modeling and Fi‐nite-Element Computation of Radial Vibration Force in Fraction‐al-Slot Permanent-Magnet Brushless Machines[J].IEEE Transac‐tions on Industry Applications,2010,46(5):1908-1918

　　[5]ZHU Z Q,XIA Z P,WU L J,et al.Influence of slot and pole num‐ber combination on radial force and vibration modes in fractional clot PM brushless machines having single-and double-layer windings[C]//2009 IEEE Energy Conversion Congress and Expo‐sition,September 20-24,2009,San Jose,CA,USA.New York:IEEE,2009:3443-3450.

　　[6]张冉,王秀和,乔东伟,等.磁极偏心削弱永磁电机激振力波方法[J].中国电机工程学报,2010,30(27):20-25.

　　[7]张冉,王秀和,乔东伟,等.基于辅助槽的永磁电机激振力波削弱方法[J].中国电机工程学报,2010,30(18):103-108.

　　[8]张冉,王秀和,乔东伟.极弧系数选择对永磁直流无刷电机激振力波的影响[J].中国电机工程学报,2010,30(21):79-85.

　　[9]于慎波,姜菲菲,王辉,等.永磁同步电主轴分数槽电机的径向电磁力分析[J].组合机床与自动化加工技术,2014(6):15-18.

　　[10]程启明,程尹曼,王映斐,等.交流电机控制策略的发展综述[J].电力系统保护与控制,2011.39(9):145-154.

　　[11]韩雪岩,李生祥,米秀峰.正弦波供电下永磁同步电动机径向电磁力波研究[J].电工电能新技术,2016,35(4):1-5.

　　[12]薛建,程振涛,彭秋阳.电主轴用宽弱磁调速范围永磁同步电机径向电磁力研究[J].机电工程技术,2019,48(8):29-32.

　　[13]康惠林,周理兵,王晋,等.多相分数槽集中绕组表贴式永磁电机谐波电流的确定及其影响[J].电工技术学报,2015,30(9):22-29.

　　[14]陈世坤.电机设计[M].北京:机械工业出版社,1983.

　　[15]杨浩东.永磁同步电机电磁振动分析[D].杭州:浙江大学,2011.