摘要：传统控制策略的有源电力滤波器在三相不平衡工况下无法快速精确检测谐波电流，会造成控制环节设计复杂以及滤波效果差的问题。为此，提出一种具有低谐波阻抗特性的三相四桥臂有源电力滤波器。通过建立三相四桥臂的平均开关模型在αβ０坐标下实现桥臂间的解耦控制。与传统的滤波器相比，该滤波器无需谐波检测环节，在三相不平衡工况下控制逆变器控制前三桥臂跟踪输出公共连接点基波正序电压，使滤波器相较负载侧呈高基波阻抗；同时，通过设计控制环节使滤波器谐波阻抗近似为０，使谐波全部通过逆变器支路流入大地，利用分流的原理实现滤波。与传统有源电力滤波器相比，该方法简化了滤波系统复杂程度同时降低了控制难度。在ＰＳＣＡＤ软件中搭建了仿真模型。结果表明：在有源电力滤波器投切后，系统侧电流三相谐波含量从２３．５７％、２５．３８％、２３．５７％降低到了０．５６％、０．８２％、０．５１％，系统侧电流基本为对称三相正弦波形，满足谐波抑制的国际标准。

　　关键词：有源电力滤波器；三相四桥臂逆变器；无谐波检测

　　ＴｈｒｅｅＰｈａｓｅＦｏｕｒＬｅｇＡｃｔｉｖｅＰｏｗｅｒＦｉｌｔｅｒｗｉｔｈＬｏｗＨａｒｍｏｎｉｃＩｍｐｅｄａｎｃｅ

　　ＴｉａｎＨａｏ，ＣｈｅｎＫｕｎｙｉ，ＫｅＸｉａｎｗａｎｇ，ＨｕａｎｇＰｅｉｘｉａｎ

　　（ＣｏｌｌｅｇｅｏｆＩｎｔｅｌｌｉｇｅｎｔＳｙｓｔｅｍｓＳｃｉｅｎｃｅａｎｄＥｎｇｉｎｅｅｒｉｎｇ，ＨｕｂｅｉＭｉｎｚｕＵｎｉｖｅｒｓｉｔｙ，Ｅｎｓｈｉ，Ｈｕｂｅｉ４４５０００，Ｃｈｉｎａ）

　　Ａｂｓｔｒａｃｔ：Ｔｒａｄｉｔｉｏｎａｌａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒｓｃａｎｎｏｔｑｕｉｃｋｌｙａｎｄａｃｃｕｒａｔｅｌｙｄｅｔｅｃｔｈａｒｍｏｎｉｃｃｕｒｒｅｎｔｓｕｎｄｅｒｔｈｒｅｅ－ｐｈａｓｅｕｎｂａｌａｎｃｅｄｃｏｎｄｉｔｉｏｎｓ，ｒｅｓｕｌｔｉｎｇｉｎｃｏｍｐｌｅｘｃｏｎｔｒｏｌｄｅｓｉｇｎａｎｄｐｏｏｒｆｉｌｔｅｒｉｎｇｐｅｒｆｏｒｍａｎｃｅ．Ｔｈｅｒｅｆｏｒｅ，ａｔｈｒｅｅ－ｐｈａｓｅｆｏｕｒｌｅｇａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒｗｉｔｈｌｏｗｈａｒｍｏｎｉｃｉｍｐｅｄａｎｃｅｃｈａｒａｃｔｅｒｉｓｔｉｃｓｉｓｐｒｏｐｏｓｅｓ．Ｄｅｃｏｕｐｌｉｎｇｃｏｎｔｒｏｌｂｅｔｗｅｅｎｂｒｉｄｇｅａｒｍｓｉｓａｃｈｉｅｖｅｄｂｙｅｓｔａｂｌｉｓｈｉｎｇａｎａｖｅｒａｇｅｄｓｗｉｔｃｈｍｏｄｅｌｏｆｔｈｅｔｈｒｅｅ－ｐｈａｓｅｆｏｕｒｌｅｇａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒ．Ｃｏｍｐａｒｅｄｔｏｔｒａｄｉｔｉｏｎａｌｆｉｌｔｅｒｓ，ｔｈｉｓｆｉｌｔｅｒｄｏｅｓｎｏｔｒｅｑｕｉｒｅｈａｒｍｏｎｉｃｄｅｔｅｃｔｉｏｎａｎｄｏｎｌｙｎｅｅｄｓｔｏｃｏｎｔｒｏｌｔｈｅｉｎｖｅｒｔｅｒｔｏｔｒａｃｋａｎｄｏｕｔｐｕｔｔｈｅｃｏｍｍｏｎｌｉｎｋｐｏｉｎｔｆｕｎｄａｍｅｎｔａｌｖｏｌｔａｇｅｏｆｔｈｅｆｒｏｎｔｔｈｒｅｅｂｒｉｄｇｅａｒｍｓ，ｍａｋｉｎｇｔｈｅｆｉｌｔｅｒｈａｖｅａｈｉｇｈｆｕｎｄａｍｅｎｔａｌｉｍｐｅｄａｎｃｅｃｏｍｐａｒｅｄｔｏｔｈｅｌｏａｄｓｉｄｅ；ａｔｔｈｅｓａｍｅｔｉｍｅ，ｂｙｄｅｓｉｇｎｉｎｇｔｈｅｃｏｎｔｒｏｌｌｉｎｋ，ｔｈｅｆｉｌｔｅｒ'ｓｈａｒｍｏｎｉｃｉｍｐｅｄａｎｃｅｉｓａｐｐｒｏｘｉｍａｔｅｌｙｚｅｒｏ，ａｌｌｏｗｉｎｇａｌｌｈａｒｍｏｎｉｃｓｔｏｆｌｏｗｉｎｔｏｔｈｅｇｒｏｕｎｄｔｈｒｏｕｇｈｔｈｅｉｎｖｅｒｔｅｒｂｒａｎｃｈ，ａｎｄｔｈｅｆｉｌｔｅｒｉｎｇｉｓｒｅａｌｉｚｅｄｂｙｕｓｉｎｇｔｈｅｐｒｉｎｃｉｐｌｅｏｆｓｈｕｎｔ．Ｔｈｅｃｏｎｔｒｏｌｌｉｎｋｉｓｓｉｍｐｌｉｆｉｅｄｃｏｍｐａｒｅｄｔｏｔｒａｄｉｔｉｏｎａｌａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒｓ．ＡｓｉｍｕｌａｔｉｏｎｍｏｄｅｌｉｓｂｕｉｌｔｉｎＰＳＣＡＤ．Ｔｈｅｒｅｓｕｌｔｓｓｈｏｗｔｈａｔａｆｔｅｒｔｈｅｓｗｉｔｃｈｉｎｇ，ｔｈｅｔｈｒｅｅ－ｐｈａｓｅｈａｒｍｏｎｉｃｃｕｒｒｅｎｔｄｅｃｒｅａｓｅｓｆｒｏｍ２３．５７％，２５．３８％ａｎｄ２３．５７％ｔｏ０．５６％，０．８２％ａｎｄ０．５１％，ａｎｄｔｈｅｓｙｓｔｅｍｓｉｄｅｃｕｒｒｅｎｔｉｓｂａｓｉｃａｌｌｙｓｙｍｍｅｔｒｉｃｔｈｒｅｅ－ｐｈａｓｅｓｉｎｅｗａｖｅｆｏｒｍ，ｗｈｉｃｈｍｅｅｔｓｔｈｅｉｎｔｅｒｎａｔｉｏｎａｌｓｔａｎｄａｒｄｏｆｈａｒｍｏｎｉｃｓｕｐｐｒｅｓｓｉｏｎ．

　　Ｋｅｙｗｏｒｄｓ：ａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒ；ｔｈｒｅｅ－ｐｈａｓｅｆｏｕｒｌｅｇｉｎｖｅｒｔｅｒ；ｎｏｈａｒｍｏｎｉｃｄｅｔｅｃｔｉｏｎ

　　０引言

　　随着我国国民经济快速发展，民商用电负荷占比越来越大，电脑、空调等大功率电器的大规模使用在电网中注入了大量的谐波。此外，由于我国低压配网多采用三相四线制的供电形式，具有三相负载分布不平衡，负载接入运行随机性大的特点，会导致配电网的电能质量恶化进而引起配电网的电能损耗增加，影响电力系统运行的经济性和安全性［１－３］。有源电力滤波器（ＡｃｔｉｖｅＰｏｗｅｒＦｉｌｔｅｒ，ＡＰＦ）由于具有高精度补偿谐波和三相不平衡的能力以及快速稳定的优点而得到了广泛应用［４－５］，它也是目前国内外研究的热点［６－８］。

　　传统控制策略的四桥臂ＡＰＦ一般采用注入式滤波，即首先通过谐波电流检测环节检测出谐波电流，而后通过控制环节控制逆变器输出相反的谐波电流分量实行滤波。但在三相四线制系统中，负载不平衡的影响会造成三相电流不平衡，传统的检测方法是检测出网侧电流的基波正序分量，之后与网侧电流进行相减，但在三相电流不平衡时，检测出的谐波电流中会包含电流的负序分量导致其无法精确地检测出电流的谐波分量［９］，造成检测失效。在此基础上有学者提出了一种瞬时无功功率原理的谐波检测法［１０］，可以在提取谐波电流时不包含负序分量，但需要对正序负序电流进行分别处理，导致检测环节设计复杂。徐岸非等［１１］提出了一种改进的ｉｐ－ｉｑ算法，但是忽略了衰减直流分量，会造成谐波检测的误差。张静等［１２］提出了一种改进的ｓ变换检测方法，但需要大量负载计算，对系统ＤＳＰ等计算环节要求过高。

　　实际上，由于检测环节一般会有锁相环和低通滤波器的存在，只要控制策略中含有检测环节就很难避免系统的误差和延迟［１３－１４］。基于此，本文提出了一种基于低谐波阻抗控制策略的四桥臂有源电流滤波器，该控制策略省去了谐波检测环节，只需跟踪公共连接点（ＰｏｉｎｔｏｆＣｏｍｍｏｎＣｏｕｐｌｉｎｇ，ＰＣＣ）基波电压，通过逆变器控制环节参数的设计选取使得ＡＰＦ呈现近似为零的谐波阻抗，使谐波通过低谐波阻抗的ＡＰＦ流入大地，实现分流式滤波。在负载三相不平衡时，第四桥臂的存在可以抑制三相不平衡对逆变器输出电压，同时对不平衡负载引起的零序电流进行补偿，保证网侧三相电压平衡便于逆变器跟踪控制。仿真实验结果证明了所提控制策略的有效性和正确性。

　　１低谐波阻抗有源电力滤波器工作原理

　　１．１分流式谐波治理原理

　　与传统注入式滤波的有源电力滤波器不同，基于谐波阻抗控制的有源电力滤波器通过分流的方式进行滤波，其基本结构如图１所示。ＡＰＦ直接并联在ＰＣＣ处，Ｕｓ为网侧等效三相电压源，ｉｈ为负载谐波电流，ｉＬ为负载侧电流，非线性负载为谐波源ｉｓ，为网侧基波电流。其中，谐波电流会通过ＡＰＦ直接流入大地。

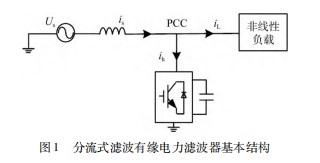
　　假设电网中负载三相平衡，Ｕｓ为理想网侧三相电压，故可取Ｕｓ中的一项进行分析。将线性负载等效为谐波源ｉｈ和阻抗ＺＬ并联，逆变器可等效为受控电压源Ｕｃ和串联阻抗ＺＦ，网侧电压源等效为基波电压源Ｕｓ和系统内阻Ｚｓ。故可得如图２所示的系统等效电路。

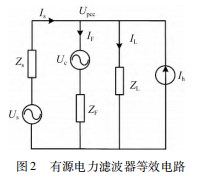
　　根据电路叠加定理可将图２拆分为基波等效电路图３（ａ）和谐波等效电路图３（ｂ）。

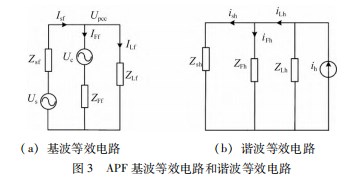
　　此时控制逆变器跟踪ＰＣＣ点基波电压，可知在基波等效电路中，由于逆变器输出电压与ＰＣＣ电压相等，此时逆变器在电路中可视为开路，基波电流全部流入负载侧。在谐波等效电路中，逆变器等效为谐波阻抗ＺＦｈ，谐波电流由负载测流出，此时只需要控制逆变器等效阻抗远远小于系统测等效谐波阻抗，由电路分流原理可知，此时谐波电流会全部通过逆变器流入大地，以此实现滤波。

　　１．２逆变器输出电压不平衡抑制原理

　　三相三线逆变器等效电路如图４所示。Ｕｃａ、Ｕｃｂ、Ｕｃｃ为逆变器输出电压，ＺＬａ、ＺＬｂ、ＺＬｃ为三相负载等效阻抗，ＺＦａ、ＺＦｂ、ＺＦｃ为逆变器等效阻抗，当三相负载平衡时，由于Ｕｃａ、Ｕｃｂ、Ｕｃｃ输出三相对称电压，ＵＧＮ为０，节点Ｎ没有电流流入。

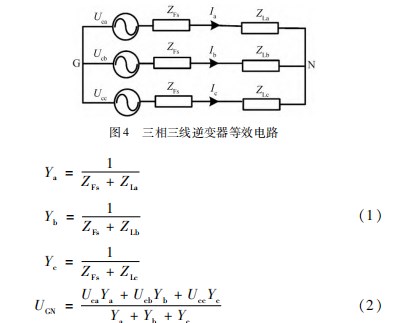
　　当三相负载不对称时，即ＺＬａ、ＺＬｂ、ＺＬｃ不全相等时，由式（２）可知，此时ＵＧＮ不为０，由于三相三线制逆变器不带中线，电流无法从节点Ｎ流出，导致Ｎ点电压发生零飘，进而导致负载上的电压发生变化，影响逆变器的输出电压。若假设逆变器输出三相对称电压，此时由于点Ｎ不流入电流，三相输出电流Ｉａ、Ｉｂ、Ｉｃ不可能对称。其本质原因便是中性点Ｎ的点位发生了漂移，导致逆变器输出电压不平衡。随着负载不平衡度的增加，其对逆变输出电压的影响程度也会增加。

　　综上，在负载不平衡工况下，为了保证逆变器输出侧得到对称的三相电压，一定会导致三相电流的不对称，为了保证流入节点的电流为０，须增加额外的电流通路。此时输出端需要有中线，为不平衡电流提供一条电流通路，以此保持ＵＧＮ为０，使得逆变器三相输出相互独立，可在不对称负载下仍然输出三相对称电压。因此，本文采用三相四桥臂逆变器，以保证在不平衡负载下三相对称电压的输出。三相四桥臂逆变器拓扑结构如图５所示。

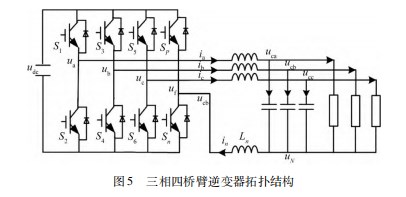
　　与传统三桥臂逆变器相比，四桥臂逆变器多了一组桥臂，本文针对上述问题，通过分离四桥臂控制功能，使第四桥臂可以在负载不平衡工况下抑制三相不平衡影响，同时对逆变器三相输出不平衡进行调节。设逆变器前三桥臂端电压为

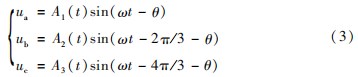
　　式中：Ａ１（ｔ）、Ａ２（ｔ）、Ａ３（ｔ）为时间ｔ的函数；θ为相角；ω为角速度。由式（３）可得：

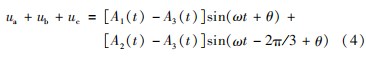
　　如果Ａ１（ｔ）＝Ａ２（ｔ）＝Ａ３（ｔ）不成立，则ｕａ＋ｕｂ＋ｕｃ不恒为０。所以当采用式（４）表示的控制命令控制逆变器时，即ｕａ＋ｕｂ＋ｕｃ恒为０，稳态时逆变器等效电路结构决定了Ａ１（ｔ）、Ａ２（ｔ）、Ａ３（ｔ）不会突变，则必会有Ａ１（ｔ）＝Ａ２（ｔ）＝Ａ３（ｔ）成立，可以保证逆变器桥臂电压三相对称。

　　由图５可得：

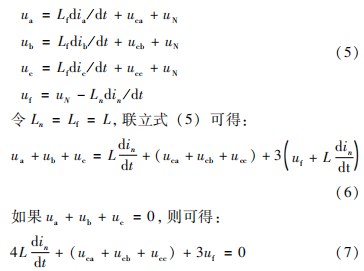
　　由式（６）～（７）可知如果控制ｕａ、ｕｂ、ｕｃ使逆变器桥臂电压三相对称，满足ｕａ＋ｕｂ＋ｕｃ＝０，则控制ｕｆ可以消除负载侧三相不平衡对逆变器输出电压的影响。此时只需要将第四桥臂的控制从前三桥臂的控制中脱离出来，通过设计前三桥臂控制环节使ｕａ＋ｕｂ＋ｕｃ＝０，之后单独通过第四桥臂控制ｕｆ即可完成系统控制环节的设计。

　　２有源电力滤波器谐波阻抗分析及控制参数确定

　　２．１四桥臂逆变器建模分析

　　为了实现第１节中所提的控制策略，实现对有源电力滤波器进行控制系统的设计，需要对有源电力滤波器在不同坐标系下的数学模型进行研究，并分析各桥臂的耦合关系。设逆变器的直流测电压Ｕｄｃ为定值，忽略死区和非线性因素的影响，就可以推导出四桥臂逆变器在ａｂｃ静止坐标系下的平均开关模型［１５］，具体如图６所示。

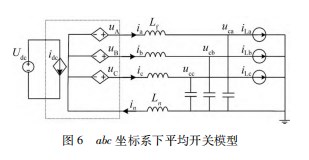
　　设三相电压占空比分别为ｄａｎ、ｄｂｎ、ｄｃｎ，可得三相逆变器输出电压为

　　根据基尔霍夫电路定律和平均开关模型可以推出系统的回路方程以及列写电容电流的表达式为：

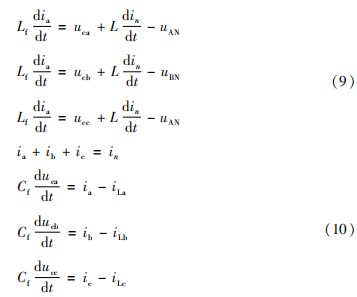
　　由式（６）可知，在ａｂｃ静止坐标系下，流过前三桥臂的电感电流均与第四桥臂的电感电流有耦合关系，同时因为逆变系统输出量均为交流量，需要在反馈控制中进行解耦处理，导致控制环节设计复杂，不便于后续控制环节的设计和ＡＰＦ等效谐波阻抗的分析。因此，把逆变器原数学模型转变成αβ０轴下的数学模型，其转化关系为：

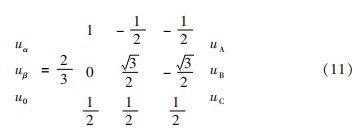
　　经过αβ０变换后可知三相桥臂在αβ０下的数学模型为：

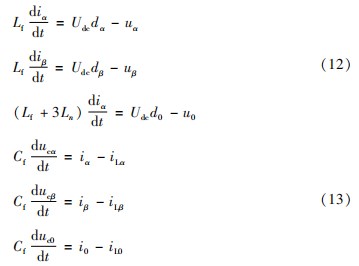
　　由式（１２）可知在αβ０坐标下ｕα、ｕβ、ｕ０之间不存在耦合关系，可实现四桥逆变器的解耦控制。由变换原理可知，当ｕＡ＋ｕＢ＋ｕＣ＝０时，０轴分量始终为０，理论上对０轴坐标的分析没有意义，但在实际应用中由于负载变化会导致输出电压波动，为保证系统稳定需要对０轴分量进行控制，即在设计控制环节的时候需对αβ０进行控制。

　　２．２基于低谐波阻抗控制策略的控制系统设计

　　根据１．１节中基于低谐波阻抗控制的ＡＰＦ工作原理可知，该控制策略的核心思想是在保持逆变器跟踪能力的前提下，尽量降低ＡＰＦ的等效谐波阻抗，以保证ＡＰＦ能有良好的滤波效果。在三相负载平衡的工况下系统侧三相电压对称，ＰＣＣ基波电压只含有正序分量，在三相不平衡的工况下ＰＣＣ基波电压不平衡，基波电压中除正序外还含有负序和零序分量。为保证控制策略的有效性同时实现对不平衡电流的补偿，在负载三相不平衡控制逆变器跟踪ＰＣＣ基波正序电压。

　　由２．１节分析可知，αβ０静止坐标系下前三桥臂与第四桥臂直接不存在耦合，因此可以对前三桥臂和第四桥臂进行分别控制。为了在逆变器控制环节能同时保证逆变器能准确跟踪输出基波电压并且保证滤波器等效谐波阻抗接近于０，采用电压外环、电流内环的双闭环对逆变器进行控制。为提高系统相应速度，电流内环采用电容电流反馈的比例控制器。由于ＰＩ控制器具有可以抑制ＬＣ滤波器谐振尖峰的特性［１６－１７］，同时ＰＩ控制器结构简单，便于分析其控制参数对滤波系统进行等效谐波阻抗的影响，外环电压控制采用比例积分控制器。

　　忽略电容电感寄生参数，采用双闭环控制策略αβ０静止坐标控制框图，如图７所示。

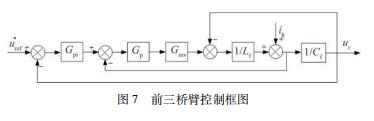
　　图７中，Ｇｐ为电压内环Ｐ控制器传递函数，Ｇｐｉ为电压外环ＰＩ控制器传递函数，Ｇｉｎｖ为逆变器增益。其中：

　　由图７可推出系统等效谐波阻抗传递函数为

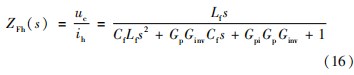
　　由式（１６）可知分母二次项系数远小于一次项，因此可忽略二次项的影响，只分析一次项系数对系统等效谐波阻抗的影响，此时只需满足式（１７），即可实现基波阻抗最小。

　　由式（１７）可知系统等效谐波阻抗主要受到Ｇｐ的影响且与Ｇｐ成反比，因此可在设计控制器时适当增加Ｇｐ的值。

　　取Ｃｆ＝６２０μＦ，Ｌｆ＝１．２ｍＨ，逆变器增益Ｇｉｎｖ＝０．７代入上式，可知Ｇｐ大于３００时便可满足系统设计要求，考虑到Ｇｐ的取值和Ｌｆ、Ｃｆ有关，为了保证系统裕度和等效谐波阻抗要求，取Ｇｐ＝４００。对于外环电压控制器，采用典型系统整定法［１８－１９］确定其参数取Ｋｐ２＝９．５、Ｋｉ＝９０９。

　　２．３第四桥臂控制

　　为简化控制环节设计难度，同时对不平衡负载引起的零序分量进行处理，对第四桥臂单独进行控制，通过控制ｕｆ抑制不平衡和非线性负载对系统的影响。由式（７）可知，要保证逆变器三相输出电压对称则需ｕｃａ＋ｕｃｂ＋ｕｃｃ＝０。

　　此时只需控制：

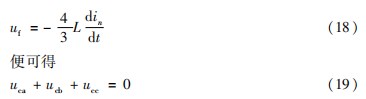
　　在实际应用中考虑到负载变化会引起电压波动，可在控制环节中加入ｋ（ｕｃａ＋ｕｃｂ＋ｕｃｃ）项提高系统的调节能力和响应速度。因此，可得第四桥臂控制信号为：

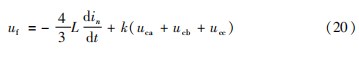
　　由式（２０）可知，第四桥臂控制指令中含有微分环节，而在实际控制器应用中，微分环节会使系统开关动作等扰动被放大，造成系统失稳［２０］。在稳态系统中，微分环节与积分环节幅值比例为ω２，相位互差１８０°。因此，可将第四桥臂中的微分项转变为积分项，最终可得第四桥臂控制信号为：

　　３仿真验证

　　为验证所提三相四桥臂有源电力滤波器控制策略的可行性和有效性，通过ＰＳＣＡＤ仿真软件搭建了真模型，其具体参数为网侧三相电压有效值Ｕｓ＝２２０Ｖ、网侧阻抗Ｚｓ＝０．３Ω、网侧基波频率ｆ＝５０Ｈｚ，同时用不可控整流桥带不对称三相阻感性负载模拟谐波源和负载侧三相不平衡工况，控制器参数按照第２．２和第２．３节中所设定的参数选取。

　　ＡＰＦ投切前系统网侧电流如图８所示，其中ｉ*ｓａ、ｉ*ｓｂ、ｉ*ｓｃ分别为补偿前系统Ａ相、Ｂ相、Ｃ相电流，可以看出在补偿前三相存在严重的不平衡和畸变。由图９所示的傅里叶分析结果可知三相网侧电流的ＴＨＤ分别为２３．５７％、２５．３８％、２３．５７％。

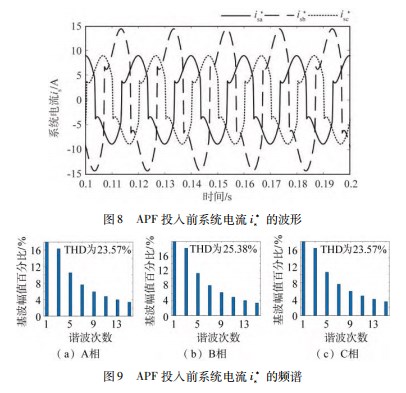
　　在ＡＰＦ接入后，系统侧三相电流ｉｓａ、ｉｓｂ、ｉｓｃ如图１０所示。此时，系统三相电流基本平衡且波形接近正弦波，由图１１所示的傅里叶分析结果可知补偿后系统三相电流ＴＨＤ为Ａ相０．５６％、Ｂ相０．８２％、Ｃ相０．５１％。

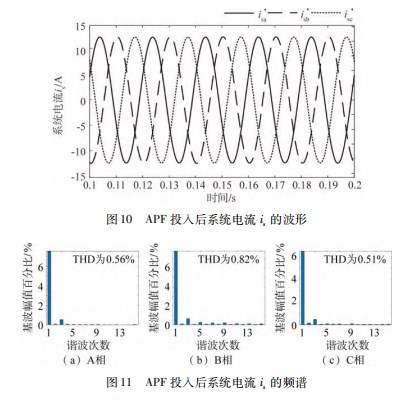
　　综上所述，在ＡＰＦ的补偿下，系统侧电流ＴＨＤ有明显下降，３～１５次谐波均得到了有效补偿，同时三相不平衡电流也得到了有效抑制。

　　４结束语

　　本文提出了一种适用于负载不平衡工况下的三相四桥臂有源电力滤波器，与传统的注入式有源电力滤波器相比，基于低谐波阻抗控制的有源电力滤波器不需要对谐波电流进行检测，只需跟踪输出ＰＣＣ基波正序电压，降低了控制系统的复杂程度。同时，由于第四桥臂的存在可以抑制负载侧不平衡对逆变器输出电压的影响，并且能对中线上的零序电流进行处理，保证逆变器可以跟踪输出对称的三相电压。在不平衡工况下通过控制跟踪ＰＣＣ点正序电压，以实现对三相不平衡电流的补偿，相较于传统的有源电力滤波器有一定的优势。仿真实验验证了所提四桥臂有源电力滤波器的有效性。

　　［１］吕正劝．中低压电网的谐波治理［Ｊ］．机电工程技术，２００８，３７（２）：７３－７６．

　　［２］李琼林，代双寅，丁同，等．基于主客观组合赋权法的低压配电网电能质量能耗综合评估［Ｊ］．电测与仪表，２０２０，５７（１２）：５２－５９．

　　［３］朱益华，郭琦，常东旭，等．谐波对电网安全稳定控制装置影响的实时仿真［Ｊ］．南方电网技术，２０１８，１２（１）：５５－６１．

　　［４］李海超，司文豪，方佳良，等．ＬＬＣＬ型具有三相不平衡补偿功能的有源电力滤波器研究［Ｊ］．电子世界，２０１８，５４７（１３）：８－１０．

　　［５］刘宏达，周磊．多功能并网逆变器及其在接入配电系统的微电网中的应用［Ｊ］．中国电机工程学报，２０１４，３４（１６）：２６４９－２６５８．

　　［６］侯世玺，汪成，付士利，等．有源电力滤波器神经终端滑模控制［Ｊ］．太阳能学报，２０２３，４４（２）：２７９－２８７

　　［７］ＤＥＳＯＵＺＡＬＬ，ＲＯＣＨＡＮ，ＦＥＲＮＡＮＤＥＳＤＡ，ｅｔａｌ．Ｇｒｉｄｈａｒｍｏｎｉｃｃｕｒｒｅｎｔｃｏｒｒｅｃｔｉｏｎｂａｓｅｄｏｎｐａｒａｌｌｅｌｔｈｒｅｅ－ｐｈａｓｅｓｈｕｎｔａｃｔｉｖｅｐｏｗｅｒｆｉｌｔｅｒ［Ｊ］．ＩＥＥＥＴｒａｎｓａｃｔｉｏｎｓｏｎＰｏｗｅｒＥｌｅｃｔｒｏｎｉｃｓ，２０２１，３７（２）：１４２２－１４３４．

　　［８］杨彦平，贾斌，李晓波．汽轮发电机组甩负荷测试及仿真分析［Ｊ］．内蒙古电力技术，２０２２，４０（３）：８０－８６．

　　［９］罗刚，钱钢，范强，等．改进型光伏并网系统谐波电流检测和补偿算法［Ｊ］．广东电力，２０２１，３４（５）：２８－３７．

　　［１０］商红桃．三相不平衡电网谐波电流检测方法的研究［Ｊ］．自动化技术与应用，２０１３，３２（１２）：７４－７７．

　　［１１］徐岸非，黄晴宇，沈磊，等．局部电网三相不平衡畸变电流补偿方法［Ｊ］．电网与清洁能源，２０２２，３８（１０）：１７－２７．

　　［１２］张静，白士贤，刁晓虹，等．一种基于改进Ｓ变换的三相不平衡检测方法［Ｊ］．电气传动，２０１９，４９（１）：８７－９０．

　　［１３］周俊，刘明，邱爱兵．基于瞬时无功功率的谐波实时检测新方法研究［Ｊ］．电力电容器与无功补偿，２０１５，３６（６）：１８－２２．

　　［１４］马永翔，权学红，闫群民等．基于ＰＩ＋ＱＰＲ控制的单相有源电力滤波器研究［Ｊ］．电测与仪表，２０２３，６０（３）：１６５－１７１．

　　［１５］ＺＨＡＮＧＲ．Ｈｉｇｈｐｅｒｆｏｒｍａｎｃｅｐｏｗｅｒｃｏｎｖｅｒｔｅｒｓｙｓｔｅｍｓｆｏｒｎｏｎｌｉｎｅａｒａｎｄｕｎｂａｌａｎｃｅｄｌｏａｄ／ｓｏｕｒｃｅ［Ｄ］．Ｂｌａｃｋｓｂｕｒｇ：ＶｉｒｇｉｎｉａＴｅｃｈ，１９９８．

　　［１６］王璨，杨明，徐殿国．基于ＰＩ控制的双惯量弹性系统机械谐振的抑制［Ｊ］．电气传动，２０１５，４５（１）：４９－５３．

　　［１７］ＪＩＡＹ，ＺＨＡＯＪ，ＦＵＸ．ＤｉｒｅｃｔｇｒｉｄｃｕｒｒｅｎｔｃｏｎｔｒｏｌｏｆＬＣＬ－ｆｉｌｔｅｒｅｄｇｒｉｄ－ｃｏｎｎｅｃｔｅｄｉｎｖｅｒｔｅｒｍｉｔｉｇａｔｉｎｇｇｒｉｄｖｏｌｔａｇｅｄｉｓｔｕｒｂａｎｃｅ［Ｊ］．ＩＥＥＥＴｒａｎｓａｃｔｉｏｎｓｏｎＰｏｗｅｒＥｌｅｃｔｒｏｎｉｃｓ，２０１４，２９（３）：１５３２－１５４１．

　　［１８］黄京，高仕红，马紫琬，等．一种隔离式三相全控型电子电力调压电源［Ｊ］．湖北民族大学学报（自然科学版），２０２２，４０（４）：４６３－４６８．

　　［１９］张兴．高等电力电子技术［Ｍ］．北京：机械工业出版社，２０１１：２．

　　［２０］周挺．改进ＰＩＤ算法在ＭＴＳ控制系统中的应用［Ｊ］．电脑知识与技术，２０２１，１７（４）：３３－３６．