摘要：传统的钻井设备未考虑外界负载变化的影响，导致稳定性差，为此，提出一种考虑外界负载变化的自调节元件响应控制方法。在设计自调节元件结构过程中，采用单锥、双锥与浅锥3种模式设计冠部结构轮廓，利用被动式液压结构反馈结构组成切削深度控制结构，通过布齿方法与布齿密度设计切削结构，完成自调节元件结构的优化。并分析自调节元件所受外部负载以及自调节元件冠部结构钻压施加情况，构建自调节元件与外部负载相互作用模型，实现自调节元件响应控制。由测试结果可知，该控制方法可减少自调节元件的磨损，提高机械转速，提升了钻井过程中钻井设备自调节元件工作状态下的稳定性，适用于复杂地质条件下的钻井作业。

　　关键词：负载变化；自调节元件；响应控制；冠部结构；切削结构；岩石硬度

　　Response Control Method of Self-Adjusting Element Considering External Load Change

　　Zhang Yujing1，Li Sheng2，Zhang Dong3

　　(1.Port College,Shandong Vocational College,Jinan 250104,China;2.Intelligent Manufacturing College,Shandong Vocational College,Jinan 250104,China;3.Drilling Technology Research Institute,Sinopec Shengli Petroleum Engineering Co.,Ltd.,Dongying,Shandong 257000,China)

　　Abstract:Traditional drilling equipment does not consider the influence of external load change,which leads to poor stability.Therefore,a response control method of self-adjusting element considering external load change is proposed.In the process of designing the structure of self-adjusting element,the crown structure profile is designed in three modes:single cone,double cone and shallow cone,the feedback structure of passive hydraulic structure is used to form the cutting depth control structure,and the cutting structure is designed by tooth arrangement method and tooth arrangement density,so that the structure of self-adjusting element is optimized.The external load on the self-adjusting element and the weight on bit of the crown structure of the self-adjusting element are analyzed,and the interaction model between the self-adjusting element and the external load is built to realize the response control of the self-adjusting element.According to the test results,this control method can reduce the wear of self-adjusting elements,increase the rotating speed of machinery,and improve the stability of self-adjusting elements of drilling equipment in the working state during drilling.It is suitable for drilling operations under complex geological conditions.

　　Key words:load change;self adjusting element;response control;crown structure;cutting structure;rock hardness

　　0引言

　　近些年，我国深探井钻井技术已进入规模应用阶段，钻井过程中钻杆和套管的磨损及防磨问题，已引起钻井界的密切关注。因此，在能源开采领域中，钻井行业中一直致力于研究黏滞问题[1]。若黏滞问题得不到及时解决，在钻井过程中的钻井设备的动态波动性容易造成钻井设备冠部区域形成破损[2]，同时对于切削深度也无法控制[3]。

　　针对这一问题，相关领域研究学者对钻井设备中所使用的自调节元件展开了研究，李琴等[4]针对硬地层环境下钻井机械的钻头出现破岩速度慢、易损坏、效率低等问题，无法满足当前的钻井效率要求，提出了硬地层中采用新型聚晶金刚石复合片(Polycrystalline Diamond Compact，PDC)齿进行破岩效率的优化。优化后的PDC齿具有脊形切削结构且可分层破碎岩石。在该研究中还采用了有限元仿真模拟方法比较了新型PDC齿与常规PDC齿破岩过程。但是，采用PDC齿进行破岩优化即使效率有所提高，但未考虑外界负载显著波动条件下切削深度的控制精度，无法彻底解决钻井过程中的元件磨损问题，因此该方法无法得以广泛的实际应用；蔡安江等[5]分析不同切削参数设备应用的影响，将剃齿径向力试验指数公式引入金属切削力理论公式中，并建立了剃齿切削力模型，获取切削参数的齿形中凹误差形成机理，通过有限元法验证了模型的有效性。但该研究忽略了机械转速对设备工作状态稳定性的影响。

　　针对以上这些问题，本文考虑外界负载变化的自调节元件响应控制方法，以期进一步全面提升钻井设备工作状态的稳定性。

　　1自调节元件响应控制方法

　　1.1自调节元件结构设计

　　1.1.1冠部结构轮廓设计

　　自调节元件的冠部结构轮廓设计过程主要包括3种轮廓模式，分别为单锥、双锥与浅锥：(1)单锥轮廓结构适用于软地层，一般情况下该类型轮廓结构配套的切削齿较大，在软地层内可提升机械转速；(2)浅锥轮廓结构为提升自调节元件的使用寿命，适用于软至中硬地层；(3)双锥轮廓结构以内锥较深和鼻部较尖为主要特征，主要应用于中硬至高硬地层。

　　依照有所差异的设计原则设计自调节元件冠部轮廓过程中，理论上冠部轮廓的冠部曲线方程式也存在差异，以等切削、等磨损与等功率为设计原则[6]，冠部曲线方程式为：

　　式中：r和rs分别为自调节元件冠部轮廓半径与切削齿s所在冠部轮廓径向距离；g和n分别为积分常数和同切削齿有所关联的试验测定指数；θ为切削齿在冠部轮廓rs处的轴向距离。

　　式(1)~(3)所示的方程均涉及到了参数rs，自调节元件冠部轮廓所使用的地层硬度同rs成正比例相关，与冠部外锥成反比例相关，即地层硬度越大，rs值越大，同时冠部外锥越短。

　　1.1.2切削结构设计

　　由于常规的非自调节元件使用过程中普遍存在易崩片、掉片与过度磨损等破损问题[7]。针对非自调节元件受损的各项特征与自调节元件应用区域的特性，在设计切削结构时以避免聚晶金刚石复合片早期损坏为目的，结合相应的布齿方法与布齿密度达到钻井复杂地层的目的。

　　(1)布齿方法

　　自调节元件中切削结构的布齿方法分布径向布置与周向布置两种方法。

　　径向布置方法是在自调节元件半径平面内依照轮廓外形布置切削齿，由此获取径向布齿图，此种布齿方法能够描述自调节元件切削结构上切削齿颈向上的布置与井底半径方向的覆盖情况[8]。依照等切削原则确定径向布齿方法，切削原则如下：

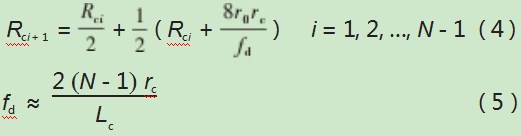
　　式中：Rci+1、Rci分别为第i+1个、第i个切削齿中心在直条机元件上的半径；fd为布齿密度系数；r0和rc分别为冠顶半径与切削齿半径；N和Lc分别为切削齿数量和冠部轮廓弧长。

　　利用式(4)与式(5)即可计算不同切削齿的径向位置，确保井底切削覆盖良好。

　　周向布置方法所描述的是在与自调节元件轴线相垂直的平面中依照相应方式布置切削齿，由此获取的周向布齿图，其能够描述自调节元件平面上切削齿布置方位情况。依照极坐标方程确定周向布齿的表达式：

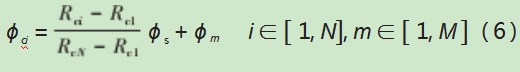
　　式中：ϕci为第m条螺旋线上第i齿的周向位置角；Rci、Rc1和RcN分别为自调节元件上第i齿、中心齿、规径齿的半径；ϕs和ϕm分别为中心齿与规径齿处的极角差与第m条螺旋线的起点极角；N和M分别为自调节元件上切削齿数量与布齿螺旋线数量。

　　基于以上表达式的描述即可计算不同切削齿的周向位置角，确保自调节元件上切削齿科学合理的布局，同时与径向布齿相结合可提升周向布齿图获取的便利性。

　　自调节元件中切削结构的两种布齿方法已经通过计算机编译为对应的软件，令自调节元件中切削结构的切削齿布置更为灵活。

　　(2)布齿密度

　　适用于复杂地层的自调节元件的布齿密度以自调节元件应用区域地层的硬度与研磨性为依据[9]，同时着重考虑区域内夹层较硬的布齿密度。同时自调节元件在复杂地层中工作时有较大概率形成不同类型的振动，导致自调节元件的鼻部与圆弧过渡区域切削齿出现崩片、掉片等破损，因此在这些易破损区域需相应地布置同轨齿提升布齿密度，同时通过双重布置聚晶金刚石复合片切削齿与TSP切削齿二次提升布齿密度，提升外部负载条件下自调节元件切削结构的抗冲击能力。

　　1.1.3切削深度控制结构设计

　　切削深度控制结构主要由被动式液压结构反馈结构组成，其中活塞杆和外界负载刚性连接[10]。在活动进入缓冲腔条件下，腔中油液面积降低，考虑油液的压缩性限制，腔内压力提升，令活塞向下运动，令其运动速度下降至停止。经由缓冲腔内油液面积调节，令切削深度控制结构适用于不同外界负载条件下负载质量与转速的标准。

　　1.2自调节元件与外部负载相互作用模型

　　1.2.1自调节元件所受外部负载分析

　　自调节元件所承受的外部负载主要来自于岩石[11]。在自调节元件应用过程中，来自于岩石的外部负载将压力施加在自调节元件上端，令自调节元件的冠部结构进入岩石内部，转盘自身自动的同时令自调节元件也随之转动，实现切削岩石的目的。由切削岩石的角度进行分析，作为岩石削切的主要环节，自调节元件同岩石间的相互作为是导致扭转振动的关键因素。

　　以βr表示自调节元件运行过程中的扭矩：

　　βc和βf分别表示作用在切削方向与摩擦方向上的力矩，两者的确定公式如下：

　　以W表示自调节元件运行过程中的外界负载：

　　式中：Uc和Uf分别为作用在切削方向与摩擦方向上的外界负载，两者的确定公式如下：

　　式中：σ为接触应力；ξ为切削面上外界负载与扭矩间的相关性。

　　将切削与摩擦相结合，利用下式描述自调节元件的阻力扭矩：

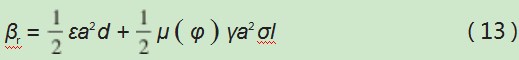
　　其作为非线性函数，自调节元件同岩石间的摩擦因数μ(φ)可通过下式描述：

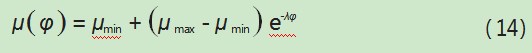
　　式中：λ为衰减系数。

　　μ(φ)在自调节元件转速提升的条件下会逐渐下降，因此在自调节元件转速处于停滞条件下的μ(φ)达到最大值。

　　1.2.2自调节元件冠部结构钻压施加分析

　　在自调节元件工作过程中，所承受的钻压是经由调节大钩提拉力进行控制[12]，在自调节元件与岩石刚接触时处于临界状态，在此条件下的自调节元件未对岩石形成压力，定义在此条件下钻杆的伸长量为临界长度s。当自调节元件进入岩石内部时其处于静态平衡状态。

　　但自调节元件在实际工作状态下，若假设轴向未发生振动，则此条件下的钻压值W(t)为：

　　式中：kc为岩石轴向刚度；d为切削齿切削深度；s为钻杆伸长量的临界长度。

　　根据自调节元件钻压与扭矩间的相关性能够得到，钻压与转盘转动是自调节元件内钻柱的输入能量，而输出则为自调节元件冠部结构的转动，其切削模型与扭转振动模型之间具有耦合相关性[13]。自调节元件冠部结构的扭转振动模型将导致其转速产生变化，由此导致自调节元件冠部结构处的钻压产生变化。自调节元件冠部结构在切削岩石过程中扭矩发生改变是导致其振动的主要因素，其值的波动导致其扭转振动参数的波动。

　　1.3自调节元件切削深度响应控制

　　根据自调节元件钻压与扭矩间的相关性，以改变切削深度来控制结构的高度和自调节元件切削齿尖端间的相对距离为核心[14]，完成自调节元件切削深度控制。在受外界负载作用形成黏/滑振动的条件下，自调节元件的控制结构伸出，有效缓解自调节元件所承受的冲击负载，降低自调节元件上切削结构承受的负载，同时稳定冠部结构，以较高的速度防止产生切削深度突变的问题。在自调节元件正常稳定应用的条件下，自调节元件上的切削深度控制结构逐步收回，对自调节元件所承受的冲击负载不产生影响[15]，由此达到理想的切削深度。自调节元件上的切削深度控制结构的伸缩由外界负载决定，实现动态调节，同时切削深度控制结构不会产生磨损问题。

　　假若钻井中包含3类硬度的岩石，其中Ⅰ类岩石为软岩石，Ⅱ类岩石与Ⅲ类岩石为高硬度岩石。Ⅰ类岩石区域内形成黏/滑的概率较低，而Ⅱ类岩石与Ⅲ类岩石区域内形成黏/滑的概率较高。相关领域研究学者的研究资源显示，在黏/滑振动形成的条件下，切削深度明显提升。

　　自调节元件上的切削深度控制结构在初始阶段处于延伸位置。在开始钻进后，受外界负载所形成的接触力影响，切削深度控制结构逐渐收缩，至瞬时切削深度最低条件下保持接触力下限为止。Ⅲ类岩石区域内形成黏/滑时，接触力点下限值即为切削深度，表现为转速曲线上的最低点。根据切削深度控制啮合曲线得到，在切削深度快速上升的条件下，被动式液压机械反馈机构不服从内向形成命令，同时啮合切削深度控制结构，形成较大的接触力，以此抵抗切削深度提升，避免黏/滑振动形成。不管黏/滑怎样发展，不同黏/滑周期均需循环抵抗或缓解黏/滑问题。在Ⅱ类岩石区域内重复上述过程，切削深度控制结构在初始阶段收缩至与Ⅱ类岩石区域切削深度。

　　Ⅰ类岩石区域与Ⅱ类岩石区域和Ⅲ类岩石区域相比切削深度值更高。切削深度控制结构在初始阶段处于延伸位置，受外界负载所形成的接触力影响后，切削深度控制结构逐渐收缩，在相应时间后接触力降至下限值。在此条件下自调节元件受给定外界负载影响能够达到快速钻进的目的。

　　2测试结果与分析

　　为验证本文所研究的考虑外界负载变化的自调节元件响应控制方法在实际自调节元件响应控制中的应用效果，选取某型号钻井设备为测试对象，将其应用于一个井深为3 km的矿井内，该矿井岩层较为复杂，具有软地层与硬地层两种不同硬度的岩石结构，分别审定不同岩石结构的硬度值，采用本文方法对测试对象进行响应控制测试，所得测试结果如下。

　　2.1自调节元件阻力扭矩变化

　　图1所示为依据矿井情况与测试对象工作参数所得的测试对象冠部区域扭矩随时间的波动情况。由图可知，测试对象冠部结构进行工作的前10 s围绕4.4 kN·m形成波动范围约为0.5 kN·m的循环波动。

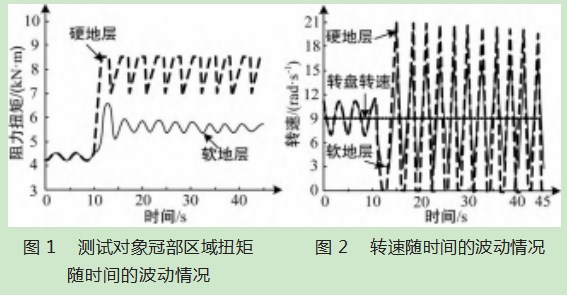
　　(1)在岩石硬度为软地层区域过渡至硬地层区域时，测试对象冠部区域的扭转形成突升现象，快速且直接提升至上限值6.72 kN·m，然后形成突降现象，快速下降至5.20 kN·m。在其后的工作过程中以5.73 kN·m的扭矩为中心，形成波动范围为0.47 kN·m的循环波动。

　　(2)在岩石硬度为硬地层时，测试对象冠部区域的扭转形成突升现象，快速且直接提升至上限8.46 kN·m后持续了约1.74 s，然后形成突降现象，快速下降至下限值7.05 kN·m，然后又逐渐提升至8.46 kN·m，并在随后的工作时间内在7.05~8.46 kN·m范围内循环波动。

　　2.2自调节元件转速变化

　　在两种不同硬度的地层条件下，测试对象冠部区域的转速随时间的波动情况如图2所示。由图可知，在测试对象工作的前10 s内，地层的硬度未出现变化，测试对象冠部区域的转速受较低的初始扰动，转速形成小范围变化。

　　(1)图2内较细的直线所描述的是软地层条件下测试对象的转速随时间的波动情况。在工作10 s后，测试对象的转速由11.17 rad/s快速下降至3.00 rad/s，随后逐渐提升至15.31 rad/s，并在其后的时间范围内以9 rad/s为中心形成循环波动。同时通过图2还能够得到，测试对象的转速形成了波动较为显著的转速变化，但并未形成测试对象转速为0的问题，也就是在此条件下未形成黏滞状态。

　　(2)图2内较粗的段状线所描述的是硬地层条件下测试对象的转速对时间的波动情况。在工作10 s后，测试对象的转速形成突降现象，由11.17 rad/s快速下降至0.00 rad/s，也就是测试对象停止工作，持续时间约为1.04 s后，测试对象再次开始工作，转速由0.00 rad/s提升至20.98 rad/s，在其后的时间范围内以9 rad/s为中心形成循环波动，且振幅随着时间延长逐渐下降。在此条件下，测试对象出现了停止工作的情况，也就是在此条件下测试对象的工作过程中形成了黏滞振动问题。

　　2.3工作条件下的稳定状态

　　对比测试对象(自调节元件)与普通元件在所应用的矿井内冠部区域的稳定边界情况，结果如图3所示。其中黑色方块、灰色方块和白色方块分别表示未形成黏滞状态、形成间歇性黏滞状态和形成持续黏滞状态。

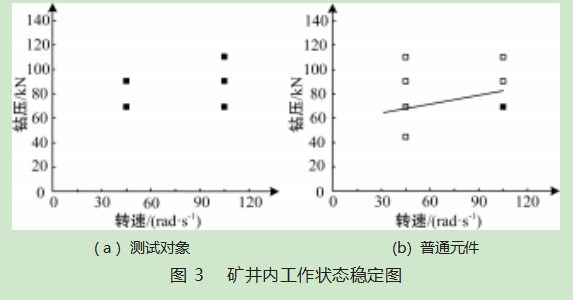
　　分析图3(a)可知，测试对象在本文方法控制下不同转速状态的工作过程中未出现黏滞问题。图3(b)内，分割白色方框与黑色方框的直线所描述的黏滞区域边界位置，由此可知，普通元件在不同转速状态的工作过程中均形成黏滞问题。由此说明本文方法控制下的测试对象在不同转速状态的工作过程中具有较高的稳定状态。

　　2.4机械能比与转速间的相关性

　　图4所示为测试对象与普通元件工作过程中的机械能比与转速间的相关性。其中黑色方块、灰色方块和白色方块分别表示未形成黏滞状态、形成间歇性黏滞状态和形成持续黏滞状态。图中左上角表示快速高效钻井，机械比能与转速分别为最低值与最高值。为提升呈现结果的清晰性，描述地面转速上限值为90 rad/s条件下的数据。

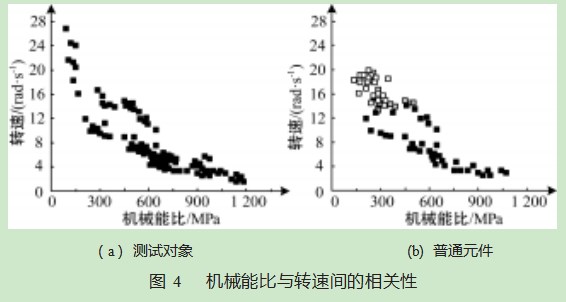
　　由此可知，在钻压较高的条件下，本文方法控制下的测试对象在机械转速达到27.2 rad/s时未形成黏滞问题。而普通元件当转速达到12 rad/s时已经呈现出间歇性黏滞状态，在转速达到13 rad/s时已经为持续黏滞状态。由此说明本文方法控制下的测试对象能够实现稳定作业，有效提升了机械转速。

　　3结束语

　　本文在考虑外界负载变化的前提下提出了一种钻进机械设备自调节元件响应控制方法，通过设计冠部结构轮廓、切削结构、切削深度控制结构，完成自调节元件结构的优化，分析自调节元件所受外部负载以及自调节元件冠部结构钻压施加情况，构建自调节元件与外部负载相互作用模型，实现自调节元件响应控制。对该控制方法下的自调节元件阻力扭矩变化、转速变化、工作条件下的稳定状态、机械能比与转速间的相关性进行了测试。测试结果表明，该自调节元件响应控制方法在复杂的地质环境下能够减少设备振动，减少自调节元件的磨损，提高机械转速，提升钻井设备的稳定性。

　　[1]查春青,柳贡慧,李军,等.PDC钻头扭转振动减振工具设计及现场应用[J].特种油气藏,2019,26(2):170-174.

　　[2]张在兴,周琴,张凯,等.岩石切削深度对切削齿温度分布的影响分析[J].煤炭学报,2019,44(S2):492-501.

　　[3]王昶皓,李士斌,张立刚.PDC破岩条件下的岩石研磨性评价[J].地质与勘探,2019,55(3):850-861.

　　[4]李琴,傅文韬,黄志强,等.硬地层中新型PDC齿破岩机理及试验研究[J].工程设计学报,2019,26(6):635-644.

　　[5]蔡安江,刘立博,刘磊,等.切削参数对剃齿切削力及齿形中凹误差的影响[J].中国机械工程,2020,31(6):655-661.

　　[6]闫炎,管志川,杨才,等.领眼与扩眼双级PDC钻头井底流场数值模拟[J].石油钻采工艺,2019,41(1):31-37.

　　[7]李思琪,田胜雷,闫铁,等.PDC钻头单齿切削天然裂缝地层断裂机理[J].东北石油大学学报,2020,44(4):22-29.

　　[8]刘春生,刘延婷,徐玉芸,等.碟盘刀具上刀齿切削煤岩的载荷特性研究[J].煤炭科学技术,2019,47(7):176-182.

　　[9]祝效华,但昭旺.PDC切削齿破碎干热岩数值模拟[J].天然气工业,2019,39(4):125-134.

　　[10]杨迎新,胡浩然,黄奎林,等.环脊式PDC钻头破岩机理实验研究[J].地下空间与工程学报,2019,15(5):1451-1460.

　　[11]邓聪颖,冯义,魏博,等.基于SVR-GA算法的广义加工空间机床切削稳定性预测与优化研究[J].仪器仪表学报,2019,40(10):227-236.

　　[12]李井辉,孙丽娜,申静波,等.基于ε-SVR的钻柱延伸能力预测技术研究[J].计算技术与自动化,2018,37(3):56-60.

　　[13]谢晗,况雨春,秦超.非平面PDC切削齿破岩有限元仿真及试验[J].石油钻探技术,2019,47(5):69-73.

　　[14]王永现,赵龙归,赵尧.自动垂直钻井工具电机驱动系统的研究[J].机电工程技术,2022,51(4):277-280.

　　[15]赵大兴,朱海峰,丁国龙,等.插齿切削模型的理论与试验研究[J].工具技术,2019,53(5):35-41.