摘要：三点法误差测量分离技术存在无法分离一阶谐波误差分量问题，四点法可以有效减小传感器读数和安装角度对回转误差分离精度的影响，但无法根除其影响。本文提供一种寻找传感器最佳安装角度的方法，以期提升回转误差分离精度。首先通过理论分析构建四点法误差测量分离技术的数学模型，找出误差传递函数，并将其作为目标寻优函数。目标函数与谐波级次数、传感器安装角度、以及权值系数相关。通过分析，在同一谐波级次下，可以将误差分离优化问题转化为路径寻优问题。将带约束的改进蚁群算法应用目标寻优过程，可以快速寻找到最佳安装角度组合，且算法能够避免陷入局部最优。仿真实验结果表明，该方法能够找寻出不同谐波级次下的最佳的传感器安装角度和权值系数，相同谐波级次下不同传感器的安装角度之间相差较大，即4个传感器基本分布在不同象限内。

　　关键词：回转误差；四点法；误差分离；蚁群算法

　　Abstract：The three－point error measurement and separation technology can not separate the first－order harmonic error components．The four－point method can effectively reduce the impact of sensor reading and installation angle on the separation accuracy of rotation error，but it can not eliminate its impact．This paper provides a method to find the best installation angle of the sensor in order to improve the separation accuracy of the rotation error．Firstly，the mathematical model of the four－point error measurement and separation technology is constructed through theoretical analysis，and the error transfer function is found out，which is used as the objective optimization function．The objective function is related to harmonic order，sensor installation angle and weight coefficient．Through analysis，under the same harmonic level，the error separation optimization problem can be transformed into a path optimization problem．Applying the improved ant colony algorithm with constraints to the goal optimization process can quickly find the best combination of installation angles，and the algorithm can avoid falling into local optimization．The simulation experiment results show that the method can find the best sensor installation angle and weight coefficient under different harmonic levels，and the installation angles of different sensors under the same harmonic level differ greatly，that is，the four sensors are basically distributed in different quadrants．

　　Key words：rotation error；four－point method；error separation；ant colony algorithm

　　0引言

　　科技进步要求零件加工精度越来越高，这就需要有加工精度更高的数控机床。提升数控机床加工精度有两种方法：一种提高数控机床本身制造水平，这种方法成本高且需要技术的不断积累；一种是测量出数控机床加工过程的回转误差，再进行误差分离，通过补偿提高加工精度，此方法成本相对较低且较易实现。

　　国内外专家学者对主轴回转误差测量、分离技术做了大量深入研究，分别提出千分表直接测量法、单点端面测量法、双点正交测量法、多点测量法等方法，其中三点法成为多点测量法误差分离技术中一个经典的误差分离方法，得到广泛应用[1]。洪迈生提出了精确的时域三点法圆度误差分离技术[2]；李自军提出了精确的频域三点法直线误差分离技术[3]；卓兴仁对三测头同方位同步测量实时分离回转误差进行了研究[4]；郭学庆[5]提出一种多圈重合三探头矩阵算法用于回转误差检测分离。三点法误差测量精度受采样点数、传感器测量精度、传感器安装角度等多重因素影响，且天然存在无法分离一阶谐波误差分量问题[6]。张宇华等学者提出再增加一个传感器(即四点法)，可以有效减小传感器读数和安装角度对回转误差分离精度的影响[7]。任宁等提出在多点法测量分离误差中，合理选择传感器间的夹角，可以使读数误差和角度误差对各次谐波检测结果的影响较小，提高测量精度[8]。杨赫然等基于四点法，提出一种基于改进遗传算法的回转误差分离技术，便于确定四侧头安装角度[9]。

　　本文对四点法测量传感器安装角度进行深入研究，通过建立误差分离模型，确定优化目标函数，在杨赫然、任宁等学者研究基础上，尝试利用改进蚁群算法进行目标寻优，找到最佳安装角度，提高误差测量分离精度。

　　1四点法误差测量分离原理

　　理想情况下，机床在加工零部件时，主轴围绕回转轴线做回转运动。但机床自身存在制造及安装误差，以及在加工时存在振动等各种因素，导致产生主轴回转误差。主轴回转误差是指主轴的实际回转轴线相对于理想回转轴线产生的偏移量，包括为径向跳动误差、轴向窜动误差、以及角度摆动误差，机床加工时三种误差共同存在、相互叠加。西安交通大学教授严晖和顾崇街把瞬时回转轴线的平均位置定义为主轴回转轴线[10]。

　　产品加工精度要求越高，机床主轴回转误差对加工尺寸影响度就越高。因此，在精密加工中要首先对回转误差精度进行测量，测量方法可分为两种，一种是利用千分表直接测量的方法，一种是利用传感器测量进行误差分离的方法。直接测量方法虽操作简便、测量成本低，但所得到的回转误差精度较低，在高精度加工领域较少使用。误差分离技术是利用传感器进行误差测量，建立误差数学模型，再利用数学方法进行信息源变换，将传感器测得的有用信号分量与误差分量进行分离。误差分离方法操作相对复杂，尤其是各测量传感器的安装位置要求非常高，但该方法的误差测量精度非常高，成为目前高精度加工领域所用的主流方法。

　　误差测量分离技术可分为单点测量法、双点测量法、多点测量法。所谓单点测量法是指使用一个传感器进行误差测量，为提升测量数据变化量的敏感度，通常将测量传感器安装在误差变化量最大的位置，此方法测量精度较低；双点测量法是指在主轴回转运动的二维平面内安装两个传感器同时测量，两个传感器可采用垂直式安装，以及对称式安装，此方法仅能分离出奇数次谐波，无法分离偶数次谐波，使用领域较窄；多点测量法是指在主轴回转运动的二维平面内安装3个或3个以上传感器进行测量，目前使用较多的是三点测量法和四点测量法。三点测量法存在一阶谐波误差分量无法分离的天然弊端，四点测量法能够解决三点测量法存在的谐波抑制问题，测量精度也大大提高，但四点测量法硬件实施较为复杂，数据计算及信息处理量急剧增加，对传感器的安装角度要求非常高。如何快速计算出四个传感器所需的安装角度，成为该领域研究的热点问题。

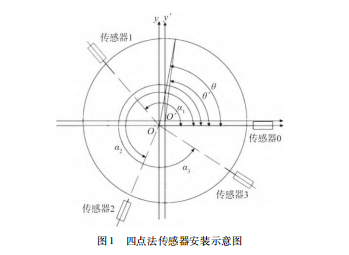
　　四点法误差分离技术是按照特定角度将4个测量传感器S0、S1、S2、S3固定于轴的径向同一端面，且到轴心距离相同，同时确保4个传感器中心线汇聚于该端面与轴线相交的中心点O，则各传感器测量输出为：

　　式中：k为谐波级次；Ak、Bk为各阶次谐波的余弦和正弦系数。

　　4个传感器测出4个误差信号，计算时将各传感器输出的信号进行加权求和，得出混合误差信号，以便进行回转误差分离。将式(1)与权值系数矩阵[c0 c1 c2 c3]相乘，将式(3)代入化简可得：

　　使用四点法进行主轴回转误差分离时，4个传感器围绕被测主轴或工件周围安装，传感器安装角度的不同，会导致测量出来的误差值产生较大差异。这一现象将会极大影响主轴回转误差测量的精度，削弱回转误差分离的效果。因此，4个传感器的安装角度成为影响回转误差分离效果的重要因素。目前，众多专家学者已经对三点法、四点法等多点法回转误差分离技术进行了深度研究，并产生了实际生产效果，提高了加工精度。但通过文献查阅可知，专家学者对于影响回转误差分离精度的最大因素——传感器安装角度和输出权值系数两个参数的研究较少，关注度较低。

　　采用四点法进行误差分离时，第一个传感器位于x轴正方向上，与x轴正方向夹角为0°，其余3个传感器均与x轴正方向成一定角度，如何找到一组最优的角度组合，使测量出的回转误差精度最小，将此问题转化为寻找四点法测量传感器的安装角度最优分布问题。假设在某个谐波级次下，选择某个高灵敏度传感器为第4个传感器，那么误差分离优化问题就转化为路径寻优问题，定义y＝q为目标优化函数，即寻找传感器最佳安装位置，以使传递函数值最小，提高误差分离精度。

　　2改进蚁群算法在误差分离技术中的应用

　　蚁群优化算法(Ant Colony Algorithm，ACO)由意大利学者Marco Dorigo于1992年首次提出，研究人员将蚁群算法用于计算机辅助选配，并探索应用于各领域，以提高产品装配精度和装配质量[11－16]。蚁群算法寻优时，蚂蚁释放的信息素可设定在路径上或节点上。本文将传感器安装角度模拟为节点以构造寻优模型，即蚂蚁信息素释放在节点上。此方法能够确保蚁群快速高效选配出最佳的安装位置，输出一套较优的安装方案，从而提高误差分离精度。

　　2.1解构造图建立

　　根据上述假设，某测量实验用四点法进行误差分离，即选用四个传感器进行回转误差测量。本文提出一种带约束的蚂蚁遍历寻优方法，将传感器Si安装中心线与x轴正方向夹角αi(α0＝0 o)作为选配依据，将c3作为约束条件。

　　如图2所示建立一个N×3矩阵，矩阵元素为某级数k下各传感器的安装角度，N为以经验值所选的各传感器安装角度的个数。第j列的所有节点组成的集合用Aj表示，每只蚂蚁将在节点aij∈Aj和节点al(j＋1)∈Aj＋1之间的路径进行寻优(寻找使y最小)，且进行单向寻优，从aij指向al(j＋1)。定义A0＝{a0}为虚拟起始点，蚂蚁从虚拟起始点开始进行寻优。

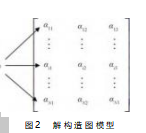
　　2.2安装角度选配的数学描述

　　蚂蚁进行遍历寻优时，在t时刻所有蚂蚁开始选择下一个临近安装角度，并在t＋1时刻同时到达。定义蚁群算法的一次迭代表示在区间(t，t＋1)内，由X只蚂蚁同时进行的X次移动，进行n次迭代后，蚁群中所有蚂蚁都进行一次完整遍历[11]。

　　定义蚂蚁在ｔ＝０时从ａ０（虚拟起始点）出发，按遍历规则（使Ｑ最小），分步选配，定义禁忌表Ｒ［Ｘ－１］［ｎ－１］，用于存储遍历到的安装角度的编号。遍历结束，禁忌表中数据即为一条完整选配链ο。在进行至第ｉ步解构造时，蚂蚁ｘ位于节点ａｉｊ上，定义ο′＝ο（ｊ）为可行部分解，即已构造好的部分节点序列，蚂蚁在约束条件下将选择访问节点ａｉｊ的可行邻域Ｎｘ（ａｉｊ）内的下一个节点ａｉ（ｊ＋１）（ａｉ（ｊ＋１）∈Ａｊ＋１）

　　2.3安装角度选配的寻优过程

　　算法寻优流程如图3所示。经过n次迭代，算出yx值，代表每只蚂蚁在安装角度间遍历长度，找到最小的ys，并记录到数据栈中。重复迭代寻优过程，直至计数器达到NCmax(设定的最大值)，算法停止。

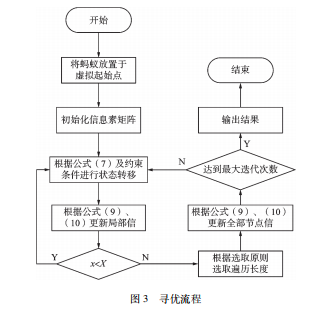
　　3仿真分析

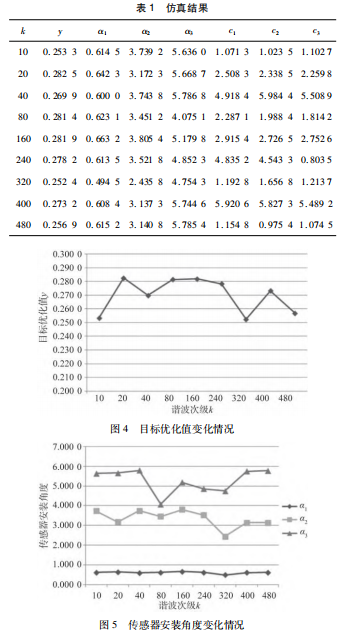
　　基于MATLAB软件进行仿真寻优过程实验，首先建立节点模式解构造图，设N＝10，在选配每一组合适的α1、α2、α3时，均需建立一个10×3的矩阵，设定最大循环次数NCmax＝100进行寻优。分别在谐波级k＝10，20，40，80，160，240，320，400，480下进行仿真，求解目标函数较优化解y，得到传感器较优安装角度、较优权值系数如表1所示。

　　在不同谐波级次k下，目标函数值y的变化规律如图4所示，由图可知，每个谐波级次下均有一组较优的传感器安装角度和传感器权值系数，从而计算出一个较优的目标优化值。各个谐波级次下较优的安装角度和权值系数均是不同的，因此目标优化值也不同，但谐波级次下的目标优化值与对应的谐波级次之间未呈现较明显的变化规律关系。此组仿真结果，谐波级次为320时，目标优化值最小(0.252 4)；谐波级次为20时，目标优化值最大(0.282 5)。随着谐波级次的增加，各级次下的目标优化值在均在(0.253，0.282)间波动，说明目标函数值受谐波级次的影响较小。

　　各谐波级次下传感器较优安装角度分布如图5所示，由图可知，传感器的较优安装角度α1、α2、α3随着谐波级次的增加均不断变化。其中α1波动范围最小，数值基本在0.6(即与x轴正方向夹角为34°)左右浮动，取值较为稳定；α2波动范围稍大，基本在3.1~3.8(即与x轴正方向夹角为178°~218°)之间变化；α3波动范围相对最大，在4.0~5.8(即与x轴正方向夹角为229°~332°)之间变动。从以上分析可知，在不同谐波级次下，α1、α2、α3各安装角度波动范围标红的大小不一样，且相同谐波级次下不同传感器的安装角度之间相差较大，即3个传感器S1、S2、S3与基本分布在不同象限内(S0位置是固定的)，与经验法实测实验总体结果趋于一致。

　　4结束语

　　随着加工精度要求越来越高，对误差分离技术的研究具有重要经济价值。本文通过对四点法误差检测分离的数学理论模型进行分析，构建了目标优化函数，将带约束的改进蚁群算法用于过程寻优。经过仿真计算，在不同的谐波级次下，均能获得较优的安装角度和权值系数，说明该方法在一定程度上能够有效的分离出误差(包括形状圆度误差和主轴回转误差)，同时对比经验值法，具备较高的精度。加工超精密零部件时，为获得超高的加工精度，通常是利用误差防止或误差补偿两种方法确保机床加工尺寸。误差防止是对机床本身零部件加工和装配进行优化，即制造超高精度的数控机床，制造成本过高，且难以实现。误差补偿技术能够通过改变数控加工程序、修改加工参数来减小误差，以较小的成本提高加工精度，实施可行性较高，本文研究结论为高精度数控机床加工的误差补偿提供了实施依据，为后续深度研究提供数据基础。

参考文献：

　　[1]金岸，缪寅宵，刘冬冬，等．主轴动态回转误差测量技术[J]．光学精密工程，2020，28(10)：2227－2243．

　　[2]洪迈生，邓宗煌，陈健强，等．精确的时域三点法圆度误差分离技术[J]．上海交通大学学报，2000(10)：1317－1319．

　　[3]李自军，洪迈生，魏元雷，等．精确的频域三点法直线误差分离技术[J]．机械设计与研究，2002(3)：54－55．

　　[4]卓兴仁，魏文宁，刘焕文，等．三测头同方位同步测量实时分离轴系回转误差[J]．计量学报，2000(2)：29－35．

　　[5]郭学庆．机床主轴动态回转误差检测技术研究[D]．沈阳：工业大学，2018．

　　[6]赵桐．机床主轴径向回转误差分离与补偿技术研究[D]．沈阳：沈阳工业大学，2021．

　　[7]张宇华，王晓琳，张国雄，等．多点法圆度及轴系误差分离方法的若干问题[J]．北京理工大学学报，1999(3)：49－53．

　　[8]任宁，宋德玉，陈岁繁．四点法圆度检测中测头最佳角位置的研究[J]．现代制造工程，2016(1)：118－123．

　　[9]杨赫然，赵桐，孙兴伟，等基于改进遗传算法的机床主轴径向回转误差分离技术研究[J]．仪器仪表学报，2021，42(1)：82－91．

　　[10]严晖，顾崇銜．再论主轴回转轴线[J]．振动．测试与诊断，1983(4)：26－27．

　　[11]刘向勇．计算机辅助选择装配的算法研究[D]．长春：吉林大学，2006．

　　[12]徐知行，刘向勇，周晓勤．基于蚁群算法的选择装配[J]．现代制造工程，2007(9)：83－85

　　[13]叶小丽，刘向勇，何展翅．基于蚁群算法的电梯导轨选择装配[J]．机电工程技术，2013，42(9)：110－114．

　　[14]刘向勇．基于改进蚁群算法的液晶拼接屏选择装配[J]．机电工程技术，2020，9(9)：110－114

　　[15]刘向勇，王鑫鹏．基于改进蚁群算法的单体电池选配技术研究[J]．数学的实践与认识，2021，51(4)：145－152．

　　[16]刘向勇．基于智能算法的计算机辅助选择装配技术[M]．重庆：重庆大学出版社，2021：43－44．