摘要:近几年，高考数学试卷中比较大小是热门题型，同时也是重点、难点，涉及到的知识主要有:作差法、作商法、找中间值法、切线放缩、不等式放缩、三角不等式、函数同构、泰勒展开式等．为了帮助学生更好地掌握“比较大小”题目的相关知识点，文章对2022年高考比较大小题目进行归纳整理，帮助学生准确理解、认识这类问题的常用解题方法．

　　关键词:比较大小的方法;同构;放缩

　　2022年全国甲卷理科第12题、2022年全国甲卷文科第12题涉及到的解法有作商法、三角不等式法、找中间值法、构造函数法及高等数学中的泰勒展开式放缩等，现就这两题给出部分解法。

　　例1(2022全国甲卷理科第12题)已知a=

　　所以b＞a．

　　例2(2022年全国甲卷文科第12题)已知9m=10，a=10m－11，b=8m－9，则()．

　　A．a＞0＞b B．a＞b＞0 C．b＞a＞0 D．b＞0＞a解法1由选项知:可找中间值法，取中间值0．

　　若a＞0，则10m－11＞0．

　　即10m＞11，m＞lg11．

　　由9m=10，得m=log9 10．

　　所以log9 10＞lg11．

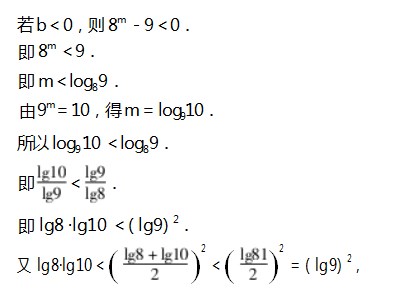
　　所以b＜0成立．

　　综上，a＞0＞b．故选A．

　　解法2由a=10m－11=10m－10－1，b=8m－9=8m－8－1，

　　可构造函数f(x)=xm－x－1，

　　此时a=f(10)，b=f(8)．

　　而f(9)=9m－9－1=9m－10=0，

　　综上，a＞0＞b．故选A．

　　通过对2022年高考比较大小题目的解法可知:要想在短时间内准确解答此类题型，必须熟练掌握相应方法，同时对一些常用的放缩，如:ex≥x+1(当且仅当x=0时等号成立);lnx≤x－1(当且仅当x=1时等号成立)，并在具体题目中归类整理，熟记一些二级结论及其变形公式，对解答此类题目都有很大帮助．

参考文献:

　　[1]盛龙．高中数学不等式解题方法探析[J]．数理化解题研究，2021(25):43－44．

　　[2]沈丽莉．高中数学学考常见不等式基本思路[J]．教育界，2021(35):10－11．

　　[3]李光星．基于高中数学基本不等式解题技巧分析[J]．数理化解题研究，2021(19):16－17．

　　[4]林秋林．“实数中的比较大小”解法探究[J]．数理天地(高中版)，2020(11):10－11+13．

　　[5]徐珊威．高中数学最值问题的解题研究[D]．昆明:云南师范大学，2020．