摘要：滑模变结构控制由于控制对象复杂，被控对象存在时空滞后和延迟性，使得滑模系统的滑模面常常不能准确地工作在理想滑模面上，引起系统抖震，制约了滑模变结构控制的实际应用。针对这一问题，在非线性积分滑模控制思想的基础上，引入了分数阶的概念，设计了一种基于分数阶的非线性积分滑模控制算法及其改进型，通过理论证明和抖震分析，基于分数阶的非线性积分滑模面可以表现出较好的控制性能，特别是减少抖震方面。最后，仿真算例验证了所提的非线性积分滑模控制方法的有效性。

　　关键词：分数阶；非线性积分；滑模算法

　　0引言

　　现代控制理论理论的重要分支之一——滑模变结构控制的研究最早要追溯到20世纪50年代末60年代初，前联学者的研究让控制理论从经典控制理论发展到现代控制理论阶段[1]。和经典控制理论相比，滑模变结构控制可以分析的控制对象更加丰富，涵盖离散系统、分布系统、非线性系统等，另外，和经典控制不同的是，滑模变结构控制系统对系统的扰动和参数变化具有鲁棒性[2]；从20世纪80年代开始，随着计算机技术、电子技术等快速发展，滑模变结构控制由于其设计方法简单，易于实现从理论阶段走向了大规模实践阶段[3]，并被大量应用于航空航天、机器人等被控对象。

　　尽管滑模变结构控制的理论研究取得了重大进展，但是由于控制对象的复杂性，特别是被控对象存在的时空滞后和延迟性，使得滑模系统的滑模面常常不能准确地工作在理想滑模面上，这就会引起系统存在抖震问题，从而大大制约了滑模变结构控制的实际应用[4]。针对这一现象，学者从两个方面进行了研究，首先就是将智能控制理论比如模糊控制等和滑模变结构控制相融合，张碧陶[5]对相关研究成果进行了总结，并提出了可以消除抖震并具有完全鲁棒性的滑模控制系统；另一种思路是采用准滑模控制的方法消除抖震，但是这种方法在一定程度上牺牲了控制系统的鲁棒性，面对这种情况，学者进一步优化改进滑模面，李鹏[6]采用一种新的饱和函数设计了一种带有非线性积分的滑模面。

　　本文在这两种思路的基础上，以一类不确定非线性系统为例，将带有非线性积分项的滑模面和分数阶微积分理论相结合，设计了一种基于分数阶的非线性积分滑模控制算法，可以在有效消除传统滑模变结构控制系统中的抖震问题的同时，改善控制系统的暂态性能。

　　1一类典型的二阶非线性系统

　　对系统(1)、(2)有如下假设：f(x,t)是不确定的有界函数，其估计函数为f~(x,t)，Δf(x,t)=f(x,t)-f~(x,t)且满足|Δf(x,t)|≤F(x,t)d(t)是外部有界干扰，满足|d(t)|≤D(t)，定义系统跟踪误差为e=y-yr，其中yr是参考信号，控制系统设计的要求就是y精确跟踪参考信号yr。

　　2非线性积分的滑模控制律设计

　　对于典型的非线性系统(1)、(2)，设计滑模控制系统和准滑模控制系统，相关的研究成果如图1所示。

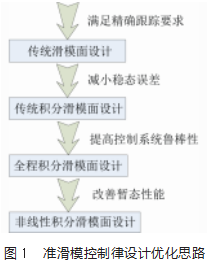
　　其中，一般滑模面设计一般形式可以表示为[7-8]：

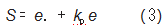
　　其中，kp>0，且为实数。这一控制律的设计可以使被控对象具有一定的鲁棒性，基本满足精确跟踪要求。

　　在式(3)中引入跟踪误差的积分项∫edτ，构成传统积分滑模面[7-8]：

　　对于式(7)~(8)所示的非线性函数有如下性质：

　　(1)若e≠0，则G(e)>0；若e=0，则G(e)=0和g(e)=0。

　　(2)G(e)是连续二次可微的，当|e|<β时，g(e)是严格单调递增函数，当|e|≥β时，g(e)饱和。

　　通过简单运算可以证明上述性质。这种非线性函数具有“小误差放大，大误差饱和”的特点，因此，可以方便地通过选择不同的β来获得期望的误差性态[10-11]。

　　3基于分数阶的非线性积分滑模控制律设计

　　3.1分数阶微积分理论基础

　　相对传统PID控制器而言，分数阶PID控制器具有许多优点：一是增加了调节自由度；二是其微分项也具有积分的功能，这种记忆功能确保了历史信息对现在和未来的影响；三是该控制器本身也是一个滤波器，能够提高控制精度和系统的稳定性。

　　3.2基于分数阶的非线性积分滑模面和控制律设计

　　在式(6)设计的一种非线性积分滑模面基础上，加以改进，设计了一种基于分数阶的非线性积分滑模面，即：

　　3.3稳定性分析

　　(1)条件1

　　这里基于李雅普诺夫(Lyapunov)稳定性理论分析滑模逼近条件。

　　3.4全局滑模性能分析

　　3.5抖震分析

　　抖震问题的存在在一定程度上极大限制了滑模变结构控制实际应用，分析其产生原因主要是由于许多工程应用中被控对象执行机构的实际相应速度远远跟不上理论响应，特别是当存在高频切换时，抖震问题会非常严重，主要表现为时间上的延迟性。分数阶系统和整数阶相比，具有更多的系统可调自由度，同时，分数阶系统自身也是一个滤波器，因此，在一定程度上消除抖震变成了可能[12-14]。

　　以图2所示的收敛过程为例进行分析。假设系统的初态为s(x0,y0)，切换面为s(x,y)=0，在控制规律的作用下，s(x0,y0)将穿越s(x,y)=0，如果执行机构响应速度很快，那么被控对象将实现很好的跟随效果，一旦执行机构响应速度较慢，被控对象需要经过一定的时间tm才能跟随。这种情况下，整数阶系统以指数etm的形式，从状态1′到状态2′再到其它状态以致在区域Δ'内来回抖动。而分数阶系统相比于整数阶系统，由于分数阶系统特殊的性能，其将以t的速度从状态1到状态2再到其他状态，以致在区域Δ内来回抖动。通过比较有Δ'>Δ，因此，如果采取分数阶系统，产生的抖震幅值将会在一定程度上减少。

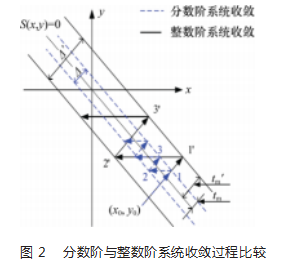
　　3.6基于分数阶的非线性积分滑模控制律等效分析

　　针对式(14)的非线性积分滑模控制律，假设输入受控，那么控制律可以表示为：

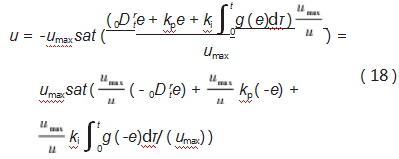
　　则上式控制律可等效为控制受限时的PDλ(分数阶比例微分)+非线性I(积分)控制。

　　3.7基于分数阶的非线性积分滑模面的进一步改进

　　在式(13)的基础上，可以对这一非线性积分滑模面进行优化，设计一种改进型的非线性积分滑模面，如下：

　　根据分数阶系统的理论，由于增加了调解的自由度，可以进一步优化非线性函数g(e)，从而在有效减少抖震的同时，进一步提升控制系统的控制性能。

　　4仿真分析

　　以典型二阶非线性系统为研究对象，通过相应的滑模变结构控制理论设计相应的滑模面，实现变结构控制。

　　比较这几种非线性滑模面的控制性能，假设考虑如下二阶非线性系统：

　　这是本文提出的一种基于分数阶非线性积分滑模控制的改进形式。非线性函数g(e)的设计参数β=0.05。

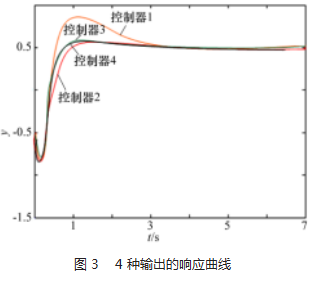
　　以上4种控制律均为“等效控制+切换项”的形式，其中边界层厚度均为u=0.2。仿真步长为0.001 s，仿真结果如图2所示。由仿真结果可知，控制器1、控制器2、控制器3和控制器4都有效消除稳态误差，控制器3和控制器4和控制器1、控制器2相比，其暂态性能更好。

　　5结束语

　　滑模变结构的被控对象存在的时空滞后和延迟性，使得滑模系统的滑模面常常不能准确工作在理想滑模面上，引起系统存在抖震问题。本文主要针对这一问题，在相应研究成果的基础上，对滑模变结构控制进行了一定的优化改进，设计了一种基于分数阶的非线性积分滑模面，通过理论证明和抖震分析，该基于分数阶的非线性积分滑模面表现出较好的控制性能，特别是减少抖震方面，但是对于复杂时延被控对象，这一控制方法仍然存在切换作用，即抖震只是得到一定削弱，并不会被消除。另外，这一控制方法是一种非线性综合方法(PDλ(分数阶比例微分)+非线性I(积分)控制)，因此，在设计控制律时，对被控对象模型具有相当一定的依赖性，也就是说系统的鲁棒性不是很强，这些问题都有待后续的进一步研究。

　　参考文献：

　　[1]V Emelyanov,N E KOstyleva.Design of variable structure control systems with discontinuous switching funetion[J].Engineering⁃Cybemeties,1964,2(1):156-160.

　　[2]O Boubaker,J P Babary.on SISO and MIMO variable structure control of nonlinear distributed Parameter systems:Application to fixed bed reactors[J].Joumal of Proces Control.2003,13(8):729-737.

　　[3]K K Shy U,W J Uu,KC Hsu.Design of large-scale time-delayed systems with dead-zone in Put via variable structure control[J].Antomatica,2005,41(7):1239-1246.

　　[4]胡跃明.变结构控制理论与应用[M].北京:科学出版社,2003.

　　[5]张碧陶.智能分数阶滑模控制及系统参数整定方法的研究[D].广州:华南理工大学,2012.

　　[6]李鹏,郑志强.非线性积分滑模控制方法[J].控制理论与应用,2011,28(3):421-425.

　　[7]CHERN T L,WU Y C.Design of integral variable structure con⁃troller and application to electrohydraulic velocity servosystems[J].IEEE Proceedings-D,1991,138(5):439-444.

　　[8]In Cheol Baik,Kyeong Hwa Kim.Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J].IEEE transactions on control systems technology:A publication of the IEEE Control Systems Society,2000,8(1):47-54.

　　[9]CHO D,KATO Y,SPILMAN D.Sliding mode and classical control⁃ler in magnetic levitation systems[J].IEEE Confirol Sysfierre Mag⁃azine,1993,13(1):42-48.

　　[10]LEE J H.Highly robust position control of BLDDSM using an improved integral variable structure systems[J].Aufiomafiica,2006,42(6):929-935.

　　[11]LU Y S.Integral variable-structure control with variable-struc⁃ture sliding dynamics for antireset windup[J].Proceedings of fihe Insfiifiution of Mechanical Engineers,Part I:Journal of Systems and Control Engineering,2008,222(3):209-216.

　　[12]OKABAYASHI R,FURUTA K.Design of sliding mode control systerns with constrained inputs[C]//Proceedings of fihe 35fih IEEE Conference on Decision and Confirol.New York:IEEE,1996:3492-3497.

　　[13]KOTHARE M V,CAMPO P J,MORARI M,et al.A unified frame⁃work for study of the anti-windup designs[J].Aufiomafiica,1994,30(12):1869-1883.

　　[14]PENG Y,VRANIR D,HANUS R.Anti-windup,bumpless,and conditioned transfer techniques for PID controllers[J].IEEE Con⁃firolstern Magazine,1996,16(4):48-57.