摘要：针对某款新能源汽车永磁同步电机在急加减速、扭矩突变等工况下，引起的噪声增大及转速变化等影响驾驶及乘坐舒适性的指标进行研究。通过对永磁同步电机进行运动及动力学建模，列出动力学方程并对其进行坐标变换及简化，得到简化及单一控制变量。基于PID搜索算法（PSA）对永磁同步电机的变频器输出电流进行控制。设计电机测试及采集设备，并通过在电机上布置的加速度传感器采集永磁同步电机阶跃载荷及冲击载荷振动加速度信号，布置在电机周围的麦克风采集电机的噪声信号，通过测功机采集转速信号，对加速度及噪声信号时域到频域进行变换。试验结果表明PSA控制方法相对于传统PID控制方法，永磁同步电机振动加速度、转速及噪声均有明显的改善，在电机3 000 r/min时加载100 N·m的阶跃扭矩时，其平均噪声由68.7 dB（A）降低到62.5 dB（A）；最大加速度由0.645 m/s2降低到0.247 m/s2，降低了61.7%，速度波动最小值由2 675 r/min升高到2 740 r/min，最大值由3 255 r/min降低到3 155 r/min。其他转速及扭矩下均有同等的改善效果，验证了该控制方法及控制模型对永磁同步电机振动抑制及噪声有明显的改善效果。

　　关键词：永磁同步电机；运动及动力方程；坐标变换；PID搜索算法；振动抑制

　　0引言

　　面对环境和能源的双重危机，汽车电驱动系统相对于传统的燃油驱动系统得到了越来越多的重视。驱动电机作为电驱动系统的关键部位，是振动噪声的主要来源。对此，国内外学者对电机振动及噪声性能做了大量研究，分析其机理，寻找优化方法。驱动电机产生电磁振动主要因素有电磁力、转矩脉动和齿槽转矩。Islam R等比较了4种不同拓扑结构的微型永磁同步电机的振动及噪声性能，最后发现电磁力才是产生噪声和振动的主要原因，而不是转矩脉动和齿槽转矩。Tao Sun等利用结构有限元分析对两种极槽组合不同的永磁同步电机进行了研究，分析了极槽配合对噪声和振动的影响。Islam M等也通过研究了几种分数槽永磁拓扑结构的径向力波，在分析极槽配合对振动噪声的影响基础上，还同时分析了绕组结构对振动噪声的影响。Qi F等推导了永磁直流电机电磁振动和声辐射公式，利用有限元法对永磁直流电机进行了切向力和谐波分析，发现切向电磁力波会是电机二阶模态的激励源，提出切向电磁力波也是引起电磁振动与噪声的主要原因。

　　本文也从永磁同步电机的结构入手，对其模型进行简化，得到其运动学及动力学模型，通过相关的坐标变换，采用PID搜索算法（PSA）对永磁同步电机电磁力的进行控制，优化新能源汽车永磁同步电机控制，减弱电机振动及噪声对驾驶及乘坐舒适性的影响。

　　1电驱系统噪声采集与处理

　　1.1测试环境搭建

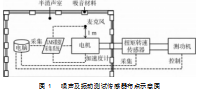
　　噪声采集场地为半消声室，以地板为反射面的消声室，是模拟半自由空间的房间，本底噪声小于15 dB（A）。采集设备采用LMS SCM2E05数据采集系统，采样频率200 kHz，保证电机在高速旋转时也能采集其精确采集电机在不同旋转角度时的噪声值，有助于模型分析。噪声及加速度信号由LMS数据采集系统进行采集，扭矩及转速信号信号通过RS485通讯方式直接读取，工控机通过TCP/IP协议连接测功机，向测功机发送指令并读取测功机的状态。测试及采集如图1所示。

　　考虑到测功机等噪声对试验结果的影响，采用通用的做法，将测功机等噪声较大的部件移出到半消声室外，以尽量消除其对测试结果的影响。

　　1.2采样工况的选择

　　针对某款新能源电机，其最大扭矩350 N·m，最大功率215 kW，减速比10.1，设计了表1所示的采样工况。考虑到电机扭矩输出特性，起步时即可输出最大扭矩，随着转速的升高，扭矩逐渐衰减，此时变为恒功率输出，故表1删除了大扭矩高转速的工况（实际上电机也无法在高转速下输出高扭矩）。测试电机在不同转速下，上位机给定一个阶跃的扭矩信号，控制测功机输出一个阶跃的扭矩，测试电机的噪声、振动加速度情况及速度波动情况。

　　2永磁同步电机控制优化

　　对永磁同步电机进行控制，需对其进行建模，根据一定的假设，对其运动及动力学方程进行简化，并对影响电机振动和噪声的关键因素进行调节及控制，以改善电机的NVH性能，提高舒适性。

　　2.1永磁同步电机动力学模型

　　永磁同步电机（PMSM）在旋转的dq坐标系中定子电压和定子磁链方程为：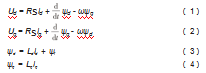

　　式中：Ud,Uq为电机d轴和q轴的定子电压；Ld,Lq为电机d轴和q轴的电枢电感；id,iq为电机d轴和q轴的电枢电流；id,iq为电机d轴和q轴的定子磁链；R s为电枢绕组电阻；ψf为永磁铁产生的磁链，是一个常量；ω为电机电角速度。

　　因为电机转子旋转一圈，每个电极均旋转一圈，故有以下公式：

　　ω=pωr（5）

　　式中：ω为电机电角速度；p为电机极对数；ωr为电机转子角速度（电机转速）。

　　由以上公式可得到如下公式：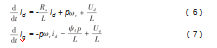

　　同步电机在旋转dq坐标系中电磁转角方程为：

　　Te=1.5p(ψdiq-ψq id)=1.5p[(Ld-Lq)id iq+ψfiq]（8）

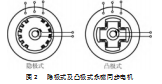
　　永磁同步电机对于隐极式电机其Ld=Lq=L，而对于凸极式电机Ld≠Lq，故对隐极式同步电机，式（8）可进一步简化为：

　　Te=1.5pψfiq（9）

　　永磁同步电机的转子动力学方程为：

　　Te-Tm-bω=J（10）

　　式中：Te为电机的电磁转矩；Tm为电机的负载扭矩；b为电机的阻尼系数；J为电机的转动惯量。

　　由式（9）和（10）可推导出：

　　状态方程为：

　　X.=AX+Bu+C（12）

　　选取X=[id iqωr]T，u=[ud uq]T由式（6）~（7）及（11）可计算出：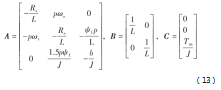

　　2.2永磁同步电机控制模型

　　由式（8）~（9）可知，p、ψf均为常数，电磁转矩方程线性化后，只需要控制电流即可控制永磁同步电机的扭矩。如图3所示为永磁同步电机典型的控制逻辑，ωr为控制器给定的速度，根据编码器反馈的角度θ的微分为永磁同步电机实际速度ωr，进行比较后运算得到需要的电流i，i为q轴给定电流，通过采集变频器的三相电流ia,ib,ic及编码器反馈的角度θ,根据变换矩阵计算出q轴实际电流iq，及d轴实际电流id，进而计算出Uq*和U，Uq*为q轴给定的电压，U为d轴给定的电压。再通过逆变换矩阵控制变频器。根据文献可得Clarke变换矩阵D，其为2行3列矩阵，非方阵，故无法对其进行求逆运算，该文献提供了一种在不改变能量大小的前提下，将其扩增为方阵E，再见过Park变换将电机q轴及d轴电流转换为变频器输出的三相电流ia,ib,ic，如式（14）。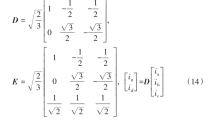

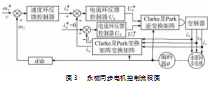
　　2.3基于PID搜索算法的永磁同步电机的控制方法。

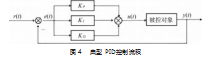
　　经典PID控制，其控制原理如图4所示。输出可以通过以下公式计算：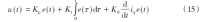

　　式中：u(t)为控制量；e(t)为偏差，即期望值与实际值之差；Kp为比例系数；Ki为积分系数；Kd为微分系数。

　　考虑到乘坐的舒服性，电机驱动输出不应有较大的波动，故采用增量式PID控制，其输出的控制量为增量，如果计算机出现故障或采集数据异常，误动作影响较小，而执行机构本身有记忆功能，可仍保持原位，不会严重影响系统的工作。对人的直观感受是平稳，无急加减速。

　　增量式PID控制的公式为：

　　Δu(t)=KpΔe(t)+KiΔe(t)+Kd(e(t)-2e(t-1)+e(t-2))（16）

　　式中：Δu(t)为当次控制量的增量的；e(t)为当次偏差；e(t-1)为上次偏差；e(t-2)为上上次偏差。

　　PID搜索算法（PID-based Search Algorithm，PSA）是一种基于PID算法的新型启发式优化算法，PID算法通过将偏差的比例P、积分I和微分D通过线性组合构成控制量，用以控制被控对象。通过不断调整系统偏差将整个群体收敛到最优状态。研究将总体的历史最佳个体（每次调节后的误差）抽象为目标值，将每个个体抽象为真值，然后模拟PID的调节过程来修正每个个体相对于最佳个体的偏差，使整个总体达到较好的状态。方法的实现方式如下。

　　（1）种群初始化

　　初始化种群可以表示为：

　　xij=(uj-lj)r1+lj（17）

　　（2）计算系统偏差

　　ek(t)=x*(t)-x(t-1)（18）

　　式中：x*(t)为对应于总体历史最小值的个体（即所有迭代后偏差最小的值）；ek(t)为当前总体偏差。

　　对增量式PID调节公式（15）改造后可得：

　　Δu(t)=Kpr2Δe(t)+Kir3Δe(t)+Kdr4(e(t)-2e(t-1)+e(t-2))（19）

　　式中：r2，r3，r4为0~1的随机数；e(t-1)为上次调整后系统总体偏差；e(t-2)为上上次调整后系统总体偏差。

　　同时为防止算法陷入局部最优，增加一个零输出条件因子，以达到总体种群均达到较好的控制水平。其定义为：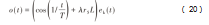

　　式中：r5为0~1的随机数。

　　其中λ根据下式更新：

　　λ=(ln(T-t+2)/ln T2（21）

　　根据式（17）、（18）、（19）可以导出PID搜索算法下一次迭代的输出值公式为：

　　x(t+1)=x(t)+ηΔu(t)+(1-η)o(t)（22）

　　式中：η=r6 cos(t/T)，r6为n行1列中的0~1的随机数矩阵。

　　可以看出基于PID搜索算法下一次的迭代输出x(t+1)是基于当次的迭代输出x(t)及当次误差Δu(t)以及零条件输出因子o(t)三个参数决定，这就最大程度地保证了输出的稳定，避免了较大的输出变化。同时，以上公式中使用的r 1、r2、r3、r4、r5、r6，均为0~1的随机数或随机矩阵，实际控制时，可以根据不同的场景，随时选择调整其数值，以适应不同场景的需求。将此控制方法应用于永磁同步电机的控制，从理论上解决了永磁同步电机的平稳输出，有助于减轻乘坐的不适感，提升新能源汽车的驾驶体验及声品质，同时较少的波动也可提升新能源汽车的寿命。

　　3测试验证

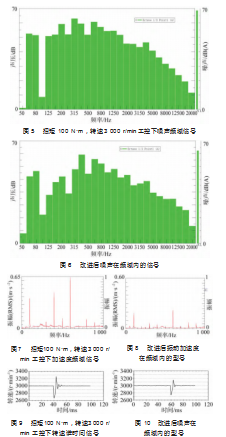
　　对传统PID控制及采用PID搜索算法（PSA）控制的永磁同步电机，均按表1的工况，在不同的转速下，电机空载且转速达到稳定的转速后，控制测功机输出对应的阶跃扭矩，同时采集永磁同步电机的振动加速度、噪声及转速信号，并对振动加速度信号及噪声信号进行频域变换。因采集工况较多，且每种工况下的数据处理方式一致，选择转速3 000 r/min时，施加100 N·m的阶跃信号（对应扭矩传感器扭矩为1 010 N·m，减速比10.1）的工况对采样数据处进行阐述，其他工况测试数据类似。图5为采用传统PID控制时，在电机转速3 000 r/min，施加100 N·m阶跃扭矩时采集在频域内的噪声信号，图6为采用PID搜索算法（PSA）控制时电机在频域内的噪声信号。图7为采用传统PID控制时电机在频域内的加速度信号，图8为采用PSA控制的电机在频域内的加速度信号。图9为采用传统PID控制时电机转速随时间信号，图10为采用PSA控制的电机转速随时间信号。

　　图5、7、9分别为采用传统PID控制时，电机的噪声、振动加速度及转速曲线。对比采用了PID搜索算法（PSA）控制的电机，如图6、8、10所示，其平均噪声由68.7 dB（A）降低到62.5 dB（A），降低了9.0%；最大加速度由0.645 m/s2降低到0.247 m/s2，降低了61.7%，速度波动最小值由2 675 r/min升高到2 740 r/min，最大值由3 255 r/min降低到3 155 r/min。在其他转速及阶跃扭矩下，其噪声、振动加速度及转速波动均有同等的优化效果，由此可见，采用PSA控制的永磁同步电机振动加速度、噪声及转速波动均有明显的降低，可有效增加驾驶员及乘客的驾驶及乘坐新能源汽车的舒适性。

　　4结束语

　　本文针对永磁同步电机的运动学方程进行变换及简化，对控制变量采用优化的控制方式，试验证明在采用传统可控制器的速度调节系统中，速度和电机转矩的超调量较大。而使用PID搜索算法可控制器的速度调节系统中，其噪声值由降低了5 dB（A）；最大加速度由0.645 m/s2降低到0.247 m/s2，降低了61.7%，速度波动最小值由2 675 r/min升高到2 740 r/min，最大值由3 255 r/min降低到3 155 r/min。速度和电机转矩曲线较平滑，振动较小，说明该控制系统具有较好的响应性和稳定性。这说明PID搜索算法具有更好的跟随性和抗扰动性，有更好的适应性和灵活性。PID搜索算法能够根据负载转矩和速度的突变，通过实时地修正参数中的随机数及随机矩阵，使其适应系统的变化，从而控制电机平稳地运行，提高新能源汽车驾驶及乘坐的舒适性。

      参考文献：

　　[1]Islam R,Husain I.Analytical model for predicting noise and vi⁃bration in permanent-magnet synchronous motors[J].IEEE Transactions on industry applications,2010,46(6):2346-2354.

　　[2]Sun T,Kim J M,Lee G H,et al.Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor[J].IEEE Transactions on magnetics,2011,47(5):1038-1041.

　　[3]Islam M S,Islam R,Sebastian T.Noise and vibration characteris⁃tics of permanent-magnet synchronous motors using electromag⁃netic and structural analyses[J].IEEE Transactions on industry applications,2014,50(5):3214-3222.

　　[4]Qi F,Wang X.Tangential force effect on the vibration and noise of PMDC motor[C]//2013 5th International Conference on Power Electronics Systems and Applications(PESA).IEEE,2013:1-5.

　　[5]Humbert L,Pellerey P,Cristaudo S.Electromagnetic and structur⁃al coupled simulation to investigate NVH behavior of an electri⁃cal automotive powertrain[J].SAE International Journal of Alter⁃native Powertrains,2012,1(2):395-404.

　　[6]尚治博.永磁同步电机模型预测电流控制策略研究[D].阜新:辽宁工程技术大学,2023.

　　[7]洪清泉,程颖.一种齿轮副模型及其在动力学仿真中的应用[J].兵工学报,2003,24(4):509-512.

　　[8]李耀华,杨启东,等.基于模糊控制的永磁同步电机动态有限状态集模型预测转矩控制[J].电机与控制学报,2021(9)[9]曹志强.电驱动总成NVH性能分析与优化[D].重庆:重庆理工大学,2020.

　　[10]潘卓.电动汽车电驱动总成机电耦合振动特性及其扭振主动控制研究[D].重庆:重庆大学,2019.

　　[11]刘泽宇.电驱动动力总成系统声品质评价维度及综合评价预测研究[D].天津:河北工业大学,2021.

　　[12]Gao Y.PID-based search algorithm:A novel metaheuristic algo⁃rithm based on PID algorithm[J].Expert Systems With Applica⁃tions,2023,232:120886.

　　[13]白钧生,冯浩,白新力,等Clarke变换中系统/2/3的推导[J].微电机,2012,45(7):79-81.

　　[14]陈荣.永磁同步电机控制系统[M].北京:中国水利水电出版社,2009.

　　[15]汪海涛,肖子涵,张世乾,等.基于参数优化的PMSM双闭环滑模控制策略研究[J].电力电子技术,2022,56(12):87-90.

　　[16]夏亮,孙天夫,李鑫宇,等.基于线性自抗扰控制技术的伺服控制系统研究[J].电气工程学报,2023,18(4):43-49.

　　[17]杨明,刘铠源,陈扬洋,等.基于PI-Lead控制的永磁同步电机双环位置伺服系统[J].电工技术学报,2023,38(8):2060-2072.

　　[18]张涵.开绕组永磁同步电机预测控制系统性能优化[D].北京:北方工业大学,2024.

　　[19]王鹏,李梁京,田久东,等.高可靠性永磁同步电机控制系统设计[J].制造业自动化,2023,45(12):131-135.

　　[20]王治国,郑泽东,李永东,等.交流电机模型预测控制综述[J].电机与控制学报,2022,26(11):14-30.

　　[21]罗世超.PMSM三矢量模型预测电流控制策略研究[D].西安:西安工业大学,2024.

　　[22]章回炫,范涛,边元均,等.永磁同步电机高性能电流预测控制[J].电工技术学报,2022,37(17):4335-4345.

　　[23]贾成禹,王旭东,周凯.基于电感辨识的内置式永磁同步电机电流模型预测控制[J].电机与控制学报,2021,25(11):75-82.