摘要：针对电子产品装配生产线效率低、堆积严重、负荷不均衡等问题，以某公司无线路由器装配生产线为例展开研究。首先，搜集生产数据，分析该生产线存在的问题；其次，基于0-1整数规划构建以最小节拍时间为目标函数的生产线平衡优化模型，该模型考虑了工序与设备、工序与工序间的关联性，以满足特殊工站的需求，并借助Lingo软件编程求解，探究通过合理分配作业工序，降低生产节拍时间，提升生产线平衡率；最后，通过AnyLogic仿真软件建立仿真模型，验证改善后方案的可靠性。验证结果表明，该方案使生产线平衡率由61.8%提高到84%，均衡系数从10.8降到3.5，单位产能由136件/h提高到185件/h，大幅提高生产效率和降低员工负荷，降低了企业生产成本和提高市场竞争力，为电子制造业提高生产线平衡率提供有效的途径。

　　关键词：生产线平衡；0-1整数规划；AnyLogic；Lingo

　　0引言

　　随着市场需求疲软、全球制造业重新分工以及人力、原材料等成本上涨，我国消费类电子产品制造业正面临较大压力。降本增效成为制造业企业发展的第一要务。加强企业内部管理，改善瓶颈工序、提高生产线平衡率是降低生产成本、提升企业效益的有效途径。

　　为解决生产线平衡问题，许多学者对此做了大量研究。生产线平衡优化方法主要有传统工业工程理论、数学精确算法如整数规划、智能优化算法如遗传算法、候鸟迁徙算法以及建模仿真方法如Anylogic仿真、Flexsim仿真。受限于单一方法的局限性，多种方法的相互结合成为当下解决生产线平衡问题的主流途径，比如传统工业工程理论和数学精确方法相结合、传统工业工程理论与智能优化算法相结合、智能优化算法和仿真建模方法相结合等。

　　对于中、小规模生产线平衡问题，传统工业工程理论与数学精确算法相结合应用广泛。Esmaeilbeigi等对SALBP-E问题提出了一种混合整数规划求解方法，并用基础数据集验证其可靠性；Akpinar等采用线性规划方法（Linear Physical Programming，LPP），以最小节拍时间、最小工作站、最小产品空闲时间差、最小空闲时间、最大生产线平衡率为优化目标，运用整数规划求解，并以实例验证该方法的优越性和科学性；刘菲以传统工业工程分析方法进行定性优化，再以最小生产节拍为目标函数构建数学模型进行定量分析，采用Lingo编程求解，大幅提高生产线平衡率；姜晨光等借助Lingo软件以SALBP-Ⅰ数学模型求解最小工作站，再以SALBP-Ⅱ数学模型求解最小节拍时间，进行组合优化，使发动机装配生产线平衡率提高至90.49%，改善效果显著。

　　在实际生产中，生产设备位置具有相对固定性，对需要使用设备的工序必须分配到相应工站上，其次，部分特殊工序具有联动性，也需要分配在同一工站上配合作业，已有的研究容易忽视工序与工序、工序与设备间的关联性。基于该类特殊问题的考虑，以某电子产品装配生产线平衡问题为例，构建0-1整数规划数学模型，再以Anylogic建立仿真模型，验证方案的可行性。

　　1生产线平衡优化理论概述

　　1.1生产线平衡理论

　　生产线平衡源于木桶定律，生产线上的瓶颈工序决定了生产线的产能。生产线平衡改善是通过合理的技术手段和方法使各个工站作业时间均衡，消除工站间的等待浪费，提高生产线整体效率。其实质是对有约束条件的有序的作业要素进行组合排序优化，是典型的NP-hard问题。

　　学术界将生产线平衡问题划分为两大类问题[15]：简单线平衡问题（Simple Assembly Line Balancing Problem，SALBP）和广义线平衡问题（General Assembly Line Bal‐ancing Problem，GALBP）。在SALBP研究中，生产线各工序总作业时间固定，其优化目标是使生产线平衡率最大化，即工作站和节拍时间乘积最小。按照工作站数量和节拍时间是否已知情况，将SALBP问题划分为SALBP-Ⅰ、SALBP-Ⅱ、SALBP-E、SALBP-F四大类。SALBP-Ⅰ问题已知节拍时间CT，求最小工作站数量m。SLABP-Ⅱ问题已知工作站数量m，求最小节拍时间CT或最小均衡系数SI。SALBP-E问题已知最小生产线节拍时间CT和最小工作站数量m，求解最大平衡率。由于节拍时间和工作站数量都未知，SALBP-E问题不再是线性模型，但可将SALBP-E问题转化为SALBP-Ⅰ或SALBP-Ⅱ问题。

　　生产线平衡评价指标主要有生产线平衡率和均衡系数。计算方法如式（1）和式（2），生产线平衡率反映了生产线各工序作业均衡状况，均衡性指数反映生产线作业时间分布状况，表明各工序作业负荷程度，其值越小，作业间的负荷差距越小，工序作业负荷越均衡。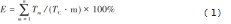

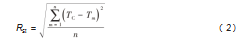
　　式中：E为生产线平衡率；RSI为均衡系数；n为工站数量；Tm为第m个工站的作业工时间；TC为节拍时间。

　　1.2基于AnyLogic的离散型系统仿真

　　离散型系统仿真是借助计算机软、硬件技术利用系统抽象模型来模拟离散型系统的运行过程，从而统计模型运行结果，总结变化规律，为管理策略提供决策支持。AnyLogic是一款基于Java语言、多方法建模的仿真软件。集成了离散事件、系统动力学、多Agent技术建模仿真方法。与其他仿真软件相比，AnyLogic仿真具有以下优势。

　　（1）内置多种建模方法和图形化显示。避免了因建模技术和方法差异而造成仿真误差，大大提高了仿真效率和准确性，其次，支持二维和三维动画展示，使仿真更直观、真实。

　　（2）扩展性强。基于Java语言，可直接导入Java、Python等插件。

　　（3）自带统计分析工具，如折线图、直方图等，可直接与Excel、数据库交互，导出仿真数据。

　　2生产线现状分析

　　某公司是一家集研发、生产、销售为一体的OEM/ODM制造商。主力产品有交换机、电力猫、无线路由器等。高端双频无线路由器是车间A主要产品，产品工艺流程具有较大相似性。WR950是该车间生产的一款高端无线路由器，此产品订单量大，具有较强的代表性。该产品工艺流程主要有插件、射频校准、组装、整机测试、包装，该生产线为直线型布局，共划分为34道作业工序，20个工位。生产线主要设备有分板机、机械臂自动测试平台、波峰焊、自动塑封机等。以此机型为例，对该生产线进行线平衡分析和改善，测定作业工时，改善生产瓶颈，提升生产线平衡率。

　　2.1确定标准作业工时

　　（1）计算观察次数

　　采用秒表测时法测定作业时间，并综合考虑作业复杂性、作业强度等，设定评比系数和宽放政策，计算标准作业时间。在现场进行秒表测时时，作业时间越短的工序在一次测时过程中产生的误差越大。观测次数越多，精度越高，观测次数可以采用误差界限法进行计算，方法如式（3）。

　　式中：ti为第i次记录的作业时间；N为最低观测次数；n为初始观测次数。

　　（2）数据可靠性检验

　　数据测量由人工完成，主观因素较大，同时，作业偶发因素也会导致数据波动，因此，有必要剔除异常值，保证数据的可靠性。常采用三倍标准差法消除异常数据。计算公式如式（4）和式（5）所示。

　　式中：为n次测验的平均值；δ为n次测验的标准差；和t都应该在3δ内。

　　（3）标准作业时间

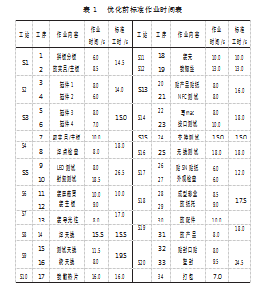
　　在确保每个工序作业时间数据可靠后，便可计算每个工序的标准作业时间。标准作业时间计算公式如式（6）。设定评比系数为1，宽放率为15%，得到每个工站的标准作业时间表，如表1所示。

　　TS=ti·γ·(1+η)（6）

　　式中：TS为标准作业时间；ti为工站观测的作业时间；γ为评比系数；η为宽放率。

　　（4）作业优先关系

　　根据产品工艺流程，绘制作业优化图如图1所示。

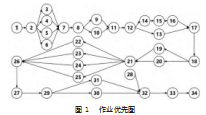
　　2.2生产线现状分析

　　根据表1可知，该生产线改善前瓶颈工时为26.5 s，总用时328 s，最长用时为26.5 s，最少用时10 s，根据式（1）和式（2）计算可知，生产线平衡率为61.8%，均衡性指数为10.8，平衡率远低于标准80%，生产线浪费严重，员工负荷极不均衡，产能为136件/h，产能严重落后，逾期交付风险高，仍具有较大改善空间。

　　3生产线平衡优化模型

　　3.1 0-1整数规划数学模型

　　Lingo软件内置强大的建模语言和多种函数，方便灵活且执行速度快，是求解优化问题的最佳选择。该生产线平衡问题属于中小规模生产线平衡问题，可以选择该软件求解。拟定假设条件如下：（1）所有工序为最小作业单元，工时已确定，且为最优工时；（2）每个工序只能分配给一个工作站，每个工作站都需要分配；（3）工序具有优先顺序；（4）允许工序存在限制，即某些工序不能放入同一工作站或某些工序需要在同一工作站；（5）该生产线上没有并行工位。

　　此数学模型有共3个基本要素：约束条件、决策变量、目标函数，根据生产线实际情况，将生产线平衡问题转换为数学模型，拟定模型各要素。

　　3.1.1模型参数

　　该数学模型中使用到的参数定义如下。i为第i个工

　　序，i=1,2,…,n；k为第k个工站，k=1,2,…,m；TC为生产节拍时间；P set为作业优先集，P set={(i,j)}表示工序i在工序j前；ti为第i个工序的作业时间。

　　3.1.2决策变量

　　作业分配过程就是工序i分配到哪个工作站k的过程，可定义0-1决策变量表示：

　　3.1.3约束条件

　　工序i必须分配到工作站k上，工序和工作站都必须分配完成：

　　Xik=1 i=1,2,…,n

　　每个工站作业时间不能超过节拍时间：

　　Xikti≤TC k=1,2,…,m

　　满足工序优先顺序，若i为j的紧前工序，当j分配到k工站时，则i工序必须分配1~k工站，不能在k工站之后：

　　∀(i,j)∈P set

　　设备位置约束，某些工序需使用设备，受设备限制，工序必须安排到相应的工站，即其决策变量为1：

　　Xef=1 e=1,2,…,n,f=1,2,…,m

　　工艺或操作原因，某些工序必须安排到同一个工站：Xrq=Xsq=1 r,s=1,2,…,n,q=1,2,…,m

　　3.1.4目标函数

　　基于SALBP-Ⅱ生产线平衡问题，即在工站数量确定的情况下，节拍时间最小，以使生产线平衡率最大。

　　min z=TC

　　综上，该问题的数学模型如下：

　　min z=TC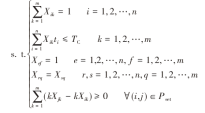

　　3.2 Lingo编程求解

　　基于各作业单元的标准作业时间和工艺优先图，在Lingo软件中编写求解程序。分板工序需使用分板设备，固定在工位1，炉后检查工序须在波峰后第1个工位，固定在第4工位，射频校准工序采用机械臂作业，固定在第5工位，即X(1,1)=1，X(7,4)=1，X(10,5)=1。塑封和打包工序使用塑封自动化设备，两工序必须同一工站，即X(33,M)=X(34,M)。运行程序，得出最优解为19.5，即生产节拍为19.5 s，Lingo求解结果如表2所示，X(i,k)=1表示第i个工序分配到第k个工站。例如X(1,1)=1表示第1个工序分配到第1个工站。

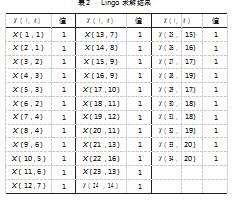
　　因生产线为直线型布局，除了上述固定工序外，其他工序可重排，在保证满足工艺流程和作业优先图下，根据表2对工站的作业单元进行重排，组建新的工站，绘制优化后的作业山积图，如图2所示。改善后生产线瓶颈时间为19.5 s，由式（1）和式（2）计算可知，生产平衡率为84%，均衡系数3.5。标准产能提升至185件/h。

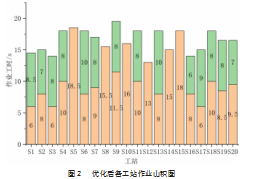
　　改善后各工站标准时间曲线比改善前更均衡，如图3所示，改善后生产平衡率比改善前提高了36%，均衡系数降低了67.5%，标准产能提高了34%，生产线负载均衡，等待浪费时间大幅减少。各指标得到进一步优化。

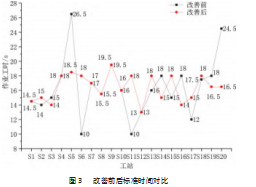
　　4基于Anylogic的生产线仿真模型

　　4.1模型参数设定

　　为了验证方案的可靠性和优越性，基于Anylogic仿真软件构建生产线仿真模型。并对运行结果进行分析和评价。

　　为了使仿真模型在最大程度上反映生产系统的真实情况，需要对生产系统用仿真语言表示。系统仿真时间单位设定为s，系统总运行时间为28 800 s（8 h），使用流程建模库和物料搬运库建立仿真模型。仿真系统中每个工站的作业时间抽象为时间的延迟，用流程库中的Delay来实现，每个工站的作业时间设定为三角分布，最小值为每个工站的最小值，最大值为每个工站的最大值，典型值为工站的平均值。同一时刻只允许1个产品加工，仿真系统中工站的等待用流程库中的Queue表示，Source表示原材料到达，由于生产瓶颈工时为19.5 s，设置间隔时间19.5 s，Sink表示产品离开仿真系统。参数id表示每个产品序列号，time()函数表示当前时间，inTime为变量，产品进入时inTime=time（），则Queue和Delay的时长为time（）-inTime，即为产品在系统等待时间和作业时间。统计产品在系统的等待时间和作业时间，并将数据保存到excel中进行分析。

　　4.2模型数据分析

　　（1）产能分析

　　产品进入系统，即Source有1 476件，Sink离开系统有1 459件，即8 h产能为1 459件，单位产能为183件/h，在制品库存为17件，单位产能比未改善前提升35%，符合企业交付需求。

　　（2）逗留时间

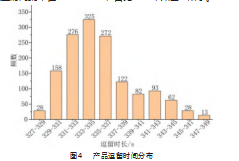
　　逗留时间是产品从进入仿真系统到离开系统所需要的总时间，包括产品加工时间和等待时间，逗留时间越小，则系统的流畅度越高，生产线效率越高。该系统平均逗留时间为334.4 s，最小逗留时间327.4 s，最长为347.8 s，完工时间集中在331~337 s，占比60%，如图4所示。

　　工站S9为瓶颈工位，平均逗留时间为22.1 s，平均作业时间为19.7 s，平均等待时间为2.4 s。生产线整体平衡率为76%。均衡系数5.8，生产线运行初期，作业均衡，没有等待现象，运行较为通畅，当生产线运行一段时间后，由于作业时间上的差异，存在等待情况。生产线各工站平均逗留时间如图5所示。

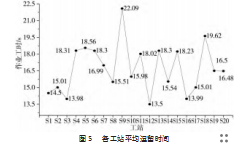
　　从产能和生产线整体平衡率来说，对比未改善前均有较大的提升，经AnyLogic仿真验证表明，改善后的方案具有优越性和可靠性。

　　5结束语

　　以无线路由器装配生产线为研究对象，分析生产线现状。为解决生产线瓶颈时间过长、等待浪费严重和负荷不均衡问题点，考虑电子产品装配生产线工序与设备、工序与工序间的关联性，基于0-1整数规划理论构建以最小化生产节拍为目标函数的数学模型，使用Lingo软件编程求解，以求解结果为依据对工序进行重排，组建新的工站，以降低工站作业时间，最后，以AnyLogic仿真软件建立仿真模型验证方案可行性，结果表明，整数规划和仿xx结合方法可以进一步提高生产线平衡率，减少生产线等待浪费时间，使各工作站作业负荷均衡，进而降低生产成本，在制造业负重前行的大背景下，为电子制造业实现生产线均衡提供了有益的借鉴。

　   参考文献：

　　[1]卞靖.全球制造业分工加速演变对我国的挑战及应对[J].中国物价,2023(9):3-6.

　　[2]戴琳琳.基于工业工程方法的汽车门线生产平衡优化[J].汽车实用技术,2022,47(7):147-151.

　　[3]李柯.基于0-1整数规划的H公司生产线平衡率优化研究[J].内燃机与配件,2018(24):143-144.

　　[4]李贻婷.基于混合算法的云制造资源配置研究[J].自动化与信息工程,2022,43(2):41-44,48.

　　[5]王科,官思佳,殷希彦,等.基于混合遗传禁忌搜索算法的混流装配线平衡优化研究[J].系统仿真学报,2023:1-13.

　　[6]李晗,范文慧,冯袁,等.基于系统动力学的汽车连杆生产线建模与仿真[J].系统仿真学报,2018,30(9):3351-3359.

　　[7]张颖,赵京鹤.基于Petri网和Flexsim模型的注塑生产线仿真与优化[J].物流技术,2023,42(8):143-148.

　　[8]郭继东,张开彬,江俊豪,等.基于程序分析和0-1整数规划模型的1号车间生产线平衡改善设计[J].机电工程技术,2020,49(2):12-16.

　　[9]陈磊,娄恒权,王相柠,等.IE与遗传算法在C公司生产线平衡中的应用研究[J].现代制造工程,2022(5):122-129.

　　[10]杨尚,施乃勇,侯智.基于Flexsim与遗传算法的混流组装线仿真与优化[J].重庆理工大学学报(自然科学),2021,35(3):86-92.

　　[11]Esmaeilbeigi.The type E simple assembly line balancing prob‐lem:A mixed integer linear programing formulation[J].Comput‐ers&Operations Research.2015,xx:168-177.

　　[12]Akpinar.A linear physical programming model for assembly line balancing problem[J].Journal of Engineering Research,2022,10(1A):316-329.

　　[13]刘菲,郑参,刘正,等.基于IE及整数规划理论的生产线平衡研究[J].现代制造工程,2021(6):101-115.

　　[14]姜晨光,严广乐.基于Lingo的发动机装配线建模优化研究[J].智能计算机与应用,2020,10(8):202-205.

　　[15]谭家兴.复杂生产线平衡问题的集成建模与求解系统研究[D].北京:北京交通大学,2021.

　　[16]裴志坚,邓志辉.基于Flexsim的D产品智能生产线平衡优化研究[J].北京工业职业技术学院学报,2023,22(4):11-15.

　　[17]龙嘉玲,张存吉,宁黎华,等.基于改进遗传算法的装配线平衡优化研究[J].机电工程技术,2023,52(8):153-156.

　　[18]孙兆琦,刘明勇,张华全.面向第Ⅱ类装配线平衡问题的蚁群-禁忌搜索混合算法[J].制造业自动化,2023,45(7):174-178.

　　[19]黄鹏鹏,邓增钰.基于Witness的生产线平衡率分析与提升[J].制造业自动化,2021,43(9):50-55.

　　[20]苗志鸿,杨明顺,xxx,等.环网柜装配线平衡改善与优化研究[J].制造业自动化,2019,41(5):34-38.