摘要：联邦学习在旋转机械故障诊断领域有着很好的发展前景，然而面对数据异构的问题，现有方法准确性严重下降。对此，提出了一种基于自适应聚类与预聚合的联邦学习框架（FLACPA）。通过改进遗传算法，实现了无需预设簇类的自适应聚类，从而得到最优的数据集群划分，此外，该框架还引入了预聚合的策略，各数据集群同时进行预聚合，通过在中介服务器上训练局部模型，有效地存储了局部信息，为联邦学习的发展提供了新的思路。在两个数据集上的实验结果表明，所提方法相较于之前联邦学习框架准确率均有提升，准确率平均提升了约2.75%。同时，该方法降低了模型训练对计算资源的需求，收敛时间最高提升了43%，显著提高了模型训练的效率。这一创新性的联邦学习框架为旋转机械故障诊断领域提供了一种有效而可行的解决方案。

　　关键词：故障诊断；联邦学习；自适应聚类；预聚合

　　0引言

　　旋转机械是工业生产中的关键设备，广泛应用于航天航空、电力、交通、林业机械、石油化工、国防工业等领域。振动故障是旋转机械在使用过程中最容易出现的故障种类之一，其不仅会制约企业的生产效率、降低产品质量，使企业蒙受巨大经济损失，甚至造成无法弥补的人员伤亡。因此，旋转机械振动故障的准确诊断意义重大。随着人工智能的迅速发展，基于深度学习的故障诊断已取得了显著的成果。卷积神经网络（CNN）、循环神经网络（RNN）、长短时记忆网络（LSTM）、生成对抗网络（GAN）等深度学习框架被广泛应用于故障诊断。以上可以看出，深度学习在数据驱动的故障诊断问题上取得了巨大成功。

　　然而在实际工业生产中，由于故障数据稀缺且隐私性较强，传统的集中式训练模型方法面临着困难。联邦学习作为一种新兴的机器学习技术，可保护用户的数据隐私。随着联邦学习的发展，逐步实现了共享特征而不是共享数据，这进一步保证了数据的隐私性。因此，联邦学习被广泛应用于故障诊断领域。文献将联邦学习与故障诊断相结合，提出一种联邦学习（FL）模型，即FL信道注意力型卷积神经网络（CA-CNN），该模型采用分层参数聚合策略对模型进行更新，仅共享模型参数，保护数据隐私。但联邦学习在处理不同参与方之间存在的数据差异性上仍需进一步优化。为了解决这一问题，文献引入了一种使用生成对抗性网络（GAN）的数据增强方案。经过训练的GAN允许每个设备本地复制来自所有设备的数据样本，从而使训练数据变得独立和同一分布（IID）。

　　与此同时，多项研究致力于在联邦学习中引入聚类技术，以进一步解决数据异构性带来的挑战，主要包括分层聚类、分阶段聚类以及迭代联合聚类。此外，文献将基于个性化聚类算法的联邦学习应用于故障诊断领域，为每个客户端订制模型参数聚合的权重,提高全局模型在每个客户端上的识别率。

　　以上聚类方法为联邦学习提供了很好的思路，但面对工况复杂的故障数据无法保证模型的准确率，此外，大量的故障数据对算力的要求较高，实际工业生产无法满足其算力需求。对此本文提出了一种基于自适应聚类与预聚合的联邦学习框架方法，主要贡献如下：（1）提出了一种自适应调整阈值的方法，通过改进遗传算法实现在不同数据分布下自适应地调整相似性阈值，进而优化聚类效果；（2）提出了预聚合的同步训练策略，引入中介服务器，针对集群进行预聚合。该策略可以降低复杂数据集对计算机的算力需求，更符合故障诊断领域的实际情况；（3）在两个旋转机械数据集上的实验验证，该方法能够解决数据异构导致的模型效果较差的问题。结果表明，该方法在故障诊断领域具有很好的应用前景。

　　1基于自适应聚类与预聚合的联邦学习框架

　　图1给出了本文提出的基于自适应聚类与预聚合的联邦学习框架整体流程，该方法主要概况为以下4个步骤：（1）通过改进遗传算法划分集群，确保每个集群具有最佳的数据相似性；（2）加入中介服务器，在不泄露隐私信息的情况下，所有集群同步预聚合；（3）预聚合后的局部模型被上传至中央服务器，通过全局聚合生成具有广泛适应性的全局模型；（4）全局模型被下发至各用户，用户结合本地数据进行进一步的个性化训练，确保模型在每个用户端都能更好地适应本地特征。

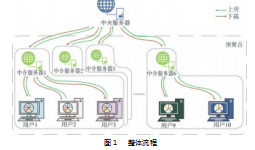
　　2关键技术

　　2.1自适应聚类

　　在联邦平均算法中，中央服务器通过加权平均来训练全局模型，这种加权方式虽然简单，但前提条件过于理想化。在实际工业领域中，各工厂故障数据分配不均衡，普通的加权平均不仅需要耗费大量的算力资源，还会影响最终的模型效果。考虑到故障数据集的规模较大且数据类别较多，本文选用遗传算法来实现用户的无监督聚类，在没有任何关于正确簇类数量的先验知识的情况下实现用户的最优划分。

　　遗传算法是一种受到进化和自然遗传原理启发的随机搜索和优化技术，在复杂、大规模和多模态的问题中能够提供接近最优解的解决方案。然而在算法执行过程中，如果种群的多样性无法得到保证，就会导致算法陷入局部最优解，错失全局最优解。在遗传算法中，交叉和变异概率直接影响算法的探索和利用能力，这就需要动态调整交叉和变异概率，确保种群保持足够的多样性，防止过早的种群收敛。本文通过对遗传算法进行改进，加入动态阈值调整，当种群多样性较低时，增加交叉概率以增加探索；当多样性足够时，减小交叉概率以增加利用，并将改进后的遗传算法应用于用户的划分，具体算法如表1所示。

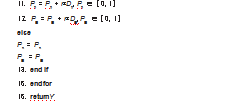
　　改进后的遗传算法具体步骤如下。

　　（1）初始化：首先设置进化代数计数器t=0，最大迭代次数为n，交叉概率Pc和变异概率Pm。此外，生成一个初始种群P，其中包含随机生成的m个个体，作为算法优化的起点。

　　（2）个体评价：对初始种群P中的每个个体进行适应度评价。适应度衡量了个体在问题空间中的优劣程度，是遗传算法进化的基础。本文综合考虑集群内的相似度和集群间的差异度，定义了适应度函数F，评价函数如下：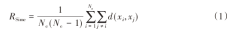

　　式（1）为集群内相似度函数。其中，RSimc为集群c内数据点之间的相似度，Nc为集群c中的数据点数，d(xi,xj)为数据点xi和xj之间的相似度度量。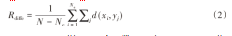

　　式（2）为集群间差异度函数。其中，Rdiffc为集群c与其他集群的差异度，N为总数据点数，Nc为集群c中的数据点数，d(xi,yj)为数据点xi和yj之间的相似度度量。

　　F=ωc⋅RSimc-ωd⋅Rdiffc（3）

　　式（3）为适应度函数F。其中，ωc和ωd为权重参数，用于平衡RSimc与Rdiffc的重要性，ωc和ωd的范围通常是[0,1]。

　　（3）选择运算：本文采用“锦标赛方案”选择出优秀的个体，使其直接遗传到下一代。

　　（4）交叉运算：通过对种群中的个体两两进行配对交叉，促使不同个体之间的信息交流，创造出具有更好特性的后代，保留种群中有价值的基因组合。交叉运算函数如下：

　　Crossover(Rparent1,Rparent2,α)

　　=α×Rparent1+(1-α)×Rparent2（4）式中：α为随机生成的值，α∈[0,1]；Rparent1和Rparent2是父代个体。

　　（5）变异运算：通过变异概率的控制，对种群中的个体进行基因的随机调整。变异操作有助于引入新的基因变化，增加种群的多样性，从而避免陷入局部最优解。变异运算函数如下：

　　Mutation(R child,Pm,r)=R child+Pm×0.1×r（5）

　　式中：R child为子代个体；Pm为变异概率，Pm∈[0,1]；r为随机生成的值，r∈[0,1]。

　　（6）更新全局最优解：对下一代的种群P new中个体进行适应度评价，这个新的种群将作为下一轮进化的起点。

　　（7）计算多样性度量：对P new中个体的多样性进行度量。通过计算个体间的多样性指标，评估算法的全局探索能力。多样性度量函数如下：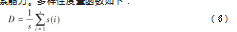

　　式中：s为种群大小；s(i)为个体i的轮廓系数。

　　s(i)函数如下：

　　式中：a(i)为个体i与同簇其他点的平均距离；b(i)为个体i与最近其他簇的平均距离。

　　D值越高，表示整体种群的个体之间差异越大，即多样性越高。

　　（8）阈值比较与参数更新：设定多样性阈值。当个体的多样性低于设定的阈值，可能表明算法陷入了局部最优解，缺乏全局探索。在这种情况下，调整算法的参数以增加探索性。交叉概率与变异概率更新函数如下：

　　Pc=Pc+r*Dc（8）

　　Pm=Pm+r*Dm（9）

　　式中：Pc为交叉概率；Pm为变异概率；Dc为交叉步长；Dm为变异步长；r为随机生成值，r∈[0,1]。

　　若个体多样性高于阈值，则表明个体多样性足够高，算法已经较好地探索了解空间，此时维持交叉概率和变异概率不变。

　　（9）得到全局最优解：经过n次迭代，逐步优化种群，找到问题空间中的最优解Y。

　　2.2预聚合

　　联邦平均算法需要在每个轮次中将模型参数从用户发送到中央服务器，然后进行聚合，整个过程涉及大量的通信开销，对计算机的算力要求较高。尤其是在故障诊断领域，数据规模巨大且类别丰富，通讯开销和时间消耗更是平常的数倍。

　　对此，本文提出了一种名为预聚合的策略。该策略引入了中介服务器，用于在信息传输到中央服务器之前在同一集群内进行局部模型参数的预先聚合。由于同一集群内的用户数据分布相似，这种预聚合能够加速模型的收敛速度。相似的数据分布意味着模型在同一集群学到的知识更具有泛化性，从而使模型更快地适应新的数据。此外，由于数据分布相似，训练模型所需的计算资源更少，从而降低了对计算机算力的需求。这一策略有效地减少了通信开销和训练时间，特别适用于大规模、丰富类别的故障诊断领域。

　　中介服务器在收到来自同一集群内的所有用户的本地聚合模型参数后，进行预聚合操作。考虑到集群数据分布相似，本文采用平均操作，中介服务器预聚合函数如下：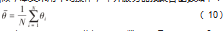

　　其中，N为同一集群内的用户数量，是预聚合后的模型参数。下一步，中介服务器将预聚合的模型参数传输给中央服务器。

　　式中：M为中介服务器的数量；All为聚合后的模型参数。

　　3实验研究
       3.1数据描述

　　（1）凯斯西储大学轴承数据集

　　凯斯西储大学（CWRU）滚动轴承数据集广泛应用于故障诊断领域，数据集包含从电机驱动端采集的振动加速度信号，采样频率为12 kHz。轴承主要有4种状态，即健康（Hea）、内圈故障（IF），外圈故障（OF）还有滚动体故障（BF）。对于每个故障状态，还包括3个级别的故障体量级别，即故障直径为7密耳，14密耳，21密耳（以密耳为单位）。同时，在转速分别为1 797、1 772、1 750和1 730 r/min的4种操作条件下收集不同健康状态下的数据。数据集在4个领域中各包含10种健康状况。

　　（2）东北林业大学数据集

　　东北林业大学数据集（NEFU-PHM）来自“XXX”型号推进减速器，减速器安装在试车台上，试车台牢牢固定在厂房地面，左侧通过电机带动转轴来推进减速器转动，试车台共设有4个振动测点，共有4路振动加速度传感器来同时采集减速器4个方位的振动信号，4个传感器测点分别位于设备的左方、右方、上方和下方。数据集由4个通道采集而成，共有6种故障状态（正常以及5种不同的故障状态），每个域下边有又根据不同的转速分为7个类别（70、75、80、85、90、95、100 r/min）。数据集在4个领域中包含6种健康状况。

　　CWRU数据集和NEFU-PHM数据集描述如表1所示。

　　3.2实验设置

　　本实验对用户本地数据的故障类别进行诊断，并对诊断任务进行评估。考虑到故障数据分布的实际情况，本文在CWRU和NEFU-PHM数据集的研究中，考虑了10个用户，各用户在各种工作条件下包含了类别齐全，缺少一种或多种类别的情况，形成了对于所有可能情况的完整覆盖。以上设置模拟了具有偏差数据的情况，符合真实的工业场景，更适用于评估真实工业环境中的模型性能。

　　3.3实验分析

　　3.3.1对比实验

　　对于CWRU和NEFU-PHM数据集，本文采用了Resnet18作为特征提取器，并采用一层全连接神经网络作为分类器。对于模型训练，本文采用了改进遗传算法（Improving Genetic Algorithm，IGA）优化器，学习率为0.01。本实验的所有方法都是在相同的环境中实现的，进行了3次试验来记录平均准确率。

　　在本文中，通过对比不同的个性化联邦学习框架，以表明所提出的FLACPA框架在故障诊断领域的有效性。具体而言，本文对比了FedAvg[17]，FedProx[18]，FedBN[19]，FedDuAp[20]四个框架，对比框架与所提框架实验设置相同。实验结果如表2所示。

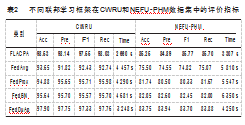
　　以上结果显示，本文提出的FLACPA框架在两个数据集上的表现均为最佳。在CWRU数据集上，FLACPA的准确率高达98.53%，其次为FedDuAp，准确率较FLACPA降低了0.63%。值得一提的是FedDuAp的耗时较其他方法少，这是由于FedDuAp对异构数据进行了不同层次的剪枝操作，减少了冗余数据的计算量，提高了效率。由于提前对用户进行自适应聚类，提高了种群的相似性，因此与FedAvg对比，FLACPA时间提升近40%，且精度提升4.88%。此外，由于FedBN在FedAvg的基础上加入了批量归一化层，因此收敛时间较FedAvg更慢，但精度稍有提升。

　　相较于CWRU数据集，上述联邦学习框架在NEFU-PHM数据集整体表现有所不同，该数据集涉及的振动故障信号工况更复杂，具体来说，CWRU数据集采样频率为12 kHz，而NEFU-PHM数据集采样频率为20 kHz，高采样频率会导致数据量增加，引入冗余信息和噪声，使得模型更容易过拟合训练数据中的细节，增加计算负担和数据处理复杂性，进而导致训练准确率下降。此外，CWRU数据集收集了3个位置的数据样本，而NEFU-PHM数据集收集了4个方向的数据样本，维度的增加可能导致维度灾难问题，即在高维空间中样本变得更为稀疏，难以准确捕捉模式和特征。在NEFU-PHM数据集上，FLACPA准确率最高，为85.25%，相较于FedAvg提升了9.75%，收敛时间提升了近43%，比CWRU数据集的提升效果更好，这说明所提出的FLACPA更适用于复杂工况的故障数据集。此外，FedDuAp的准确率和训练时间都位于第二，FedBN的收敛时间最长，比FLACPA高了近一倍。

　　本文接着在两个数据集上进行了聚类方法的对比实验，验证了基于改进遗传算法的自适应聚类在故障数据集上的优越性。实验结果如图2~3所示。

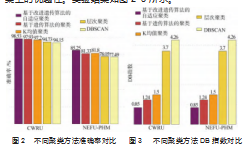
　　本文用准确率和Davies-Bouldin（DB）指数两个评价指标来对比上述聚类方法。其中，DB指数通过计算各簇之间的平均相似性和簇的半径之和来评估聚类效果。从图中可以看出，本文提出的基于改进遗传算法的自适应聚类在两个数据集上的表现均为最佳。在CWRU数据集上，基于遗传算法的聚类效果次之，第三是K均值聚类，二者差距并不大，说明二者都更擅长处理大规模数据集，层次聚类和DBSCAN在处理大规模数据集上反而效果较差。在NEFU-PHM数据集上，本文提出的方法DB指数明显升高，说明应对工况更复杂的数据集时，所提方法的聚类效果也会受到影响。与CWRU数据集不同的是，K均值聚类的表现比基于遗传算法的聚类更好，但是K均值聚类需要提前设置聚类数量，这无疑增大了试错的工作量。总体来说，不论是效果最好的自适应聚类还是效果最差的DBSCAN，都比FedAvg的准确率高，这也从侧面反映了本文所提出的聚类后再训练的策略具有一定的优越性。

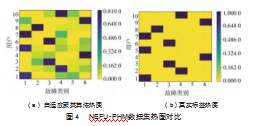
　　此外，本文还将NEFU-PHM数据集上聚类热图与真实标签热图进行对比，如图4所示。其中深色为最大占比故障类别。可以较为明显地看出，自适应聚类算法可以准确地识别故障数据特征，判断出用户所拥有的故障类别，实现用户的精准聚类。

　　3.3.2消融实验

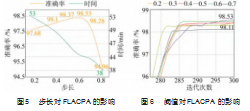
　　本研究针对步长对模型效果的影响进行了消融实验。具体来说，步长较大可以使算法快速收敛，同时避免陷入局部最优解；步长较小有助于在搜索空间做更精细的调整，更适用于复杂数据集。因此，本研究通过改变步长，评估模型的效果。本研究在CWRU数据集上进行实验，实验结果如图5所示。从图中可以看出，步长从0.2~0.6，准确率逐步升高，最高达到98.53%，说明较小的步长有助于在搜索空间中进行更细致的探索，导致准确率的提升。当步长为0.7时准确率开始下降，0.8时骤降至94.96%，说明随着步长的逐渐增大，算法过快地跳过最优解，导致模型参数偏离最优值，从而准确率下降。

　　从时间来看，随着步长的增大，模型收敛的时间逐渐降低，这是由于较大的步长促使算法更快速地收敛到全局最优解，从而减少了训练的迭代次数。这意味着模型参数更迅速地在参数空间中移动，可能更早找到最优解并跨越平坦区域，从而降低了梯度下降的步骤和训练的总体时间。

　　在本研究中，观察到当步长设置为0.6时，模型表现出最高的准确率并在相对较短的时间内完成训练，因此综合考虑，将其认定为步长的最优超参数。

　　此外，本文还研究了阈值对模型效果的影响，在CWRU数据集上的实验结果如图6所示。可以较为明显地看出，当阈值小于0.6时模型的准确率一直高于98.3%，其中阈值为0.5时模型的准确率最高，继续升高阈值，准确率反而降低。这是由于阈值设置过高，导致增加种群多样性的频率降低，种群过早收敛，陷入局部最优解。此外，模型收敛时间与阈值呈负相关，当阈值较低时，增加种群多样性的频率高，所涉及的计算量也随之增大；反之，当阈值较高时，由于更新交叉概率和变异概率的概率降低，算法会更快速地收敛，模型的探索能力也随之降低。

　　4结束语

　　本文针对故障诊断领域中用户数据异构问题，提出了一种创新性的联邦学习框架。该框架对遗传算法进行改进，创建了更适合复杂数据集的自适应聚类方法，可以在未知簇类的情况下划分最优集群，实现对用户的有效分组，尽可能地降低异构数据对模型训练效果的影响。同时，本文引入了预聚合的策略，在传统联邦学习框架中加入中介服务器，预先聚合种群的局部模型。此外，通过分组、分层训练模式，减小了对计算机算力的需求，提高了模型的收敛效率，显著减少了模型聚合时间。综上，本文提出的联邦学习框架充分利用了自适应聚类和预聚合的优势，可为复杂工况下的数据异构问题提供高效且可行的解决方案。

　    参考文献：

　　[1]Zhang R,Gu Y.A transfer learning framework with a one-dimen‐sional deep subdomain adaptation network for bearing fault diag‐nosis under different working conditions[J].Sensors,2022,22(4):1624.

　　[2]范国栋,李博涵.基于机器学习的工业机械设备故障预测方法[J].自动化与信息工程,2023,44(4):13-18,50

　　[3]ZHANG J,SUN Y,GUO L,et al.A new bearing fault diagnosis method based on modified convolutional neural networks[J].Chi‐nese Journal of Aeronautics,2020,33(2):439-447.

　　[4]Shenfield A,Howarth M.A Novel Deep Learning Model for the Detection and Identification of Rolling Element-Bearing Faults[J].Sensors,2020,20(18):5112.

　　[5]LIU G,GU H,SHEN X,et al.Bayesian long short-term memory model for fault early warning of nuclear power turbine[J/OL].IEEE Access,2020,8:50801-50813.DOI:10.1109/AC‐CESS.2020.2980244.

　　[6]Tao H,Wang P,Chen Y,et al.An unsupervised fault diagnosis method for rolling bearing using STFT and generative neural networks[J].Journal of the Franklin Institute,2020,357(11):7286-7307.

　　[7]Jiao J,Zhao M,Lin J,et al.Deep coupled dense convolutional network with complementary data for intelligent fault diagnosis[J].IEEE Transactions on Industrial Electronics,2019,66(12):9858-9867.

　　[8]刘子豪,陈浩棠,钱尚斌.基于区块链的快时尚供应链联邦共享平台[J].机电工程技术,2022,51(8):40-43.

　　[9]Zhang W,Li X,Ma H,et al.Federated learning for machinery fault diagnosis with dynamic validation and self-supervision[J].Knowledge-Based Systems,2021,213:106679.

　　[10]Lin J,Ma J,Zhu J.Hierarchical federated learning for power transformer fault diagnosis[J].IEEE Transactions on Instrumen‐tation and Measurement,2022,71:1-11.

　　[11]Jeong E,Oh S,Kim H,et al.Communication-efficient on-device machine learning:Federated distillation and augmentation under non-iid private data[J].arXiv preprint arXiv:1811.11479,2018.

　　[12]F Sattler,KR Müller,W Samek.Clustered federated learning:Model-agnostic distributed multitask optimization under priva‐cy constraints[J].IEEE TNNLS,2020,32(8):3710-3722.

　　[13]C Briggs,Z Fan,P Andras.Federated learning with hierarchical clustering of local updates to improve training on non-IID data[J].IJCNN,2020:1–9.

　　[14]Kim Y,Al Hakim E,Haraldson J,et al.Dynamic clustering in federated learning[C]//ICC 2021-IEEE International Confer‐ence on Communications.New York:IEEE,2021.

　　[15]AGhosh,J Chung,D Yin.An efficient framework for clustered federated learning[J].NeurIPS,2020(33):19586-19597.

　　[16]柳秀.基于深度学习的航空发动机附件机匣故障诊断研究[D].哈尔滨:哈尔滨理工大学,2024.

　　[17]McMahan B,Moore E,Ramage D,et al.Communication-effi‐cient learning of deep networks from decentralized data[C]//Arti‐ficial intelligence and statistics.PMLR,2017.

　　[18]Li T,Sahu A K,Zaheer M,et al.Federated optimization in het‐erogeneous networks[J].Proceedings of Machine Learning and Systems,2020(2):429-450.

　　[19]Li X,Jiang M,Zhang X,et al.Fedbn:Federated learning on non-iid features via local batch normalization[J].arXiv preprint arXiv:2102.07623,2021.

　　[20]Zhang H,Liu J,Jia J,et al.Fedduap:Federated learning with dynamic update and adaptive pruning using shared data on the server[J].arXiv preprint arXiv:2204.11536,2022.