摘要：家禽养殖时，影响家禽生存状态的因素很多，其中最直接的因素是温度。由于温度控制的滞后性比较大，温度控制的要求不同，控制参数和设定要求存在差异。针对不同环境下的控制要求，结合普通PID的控制调节方式，提出一种能普遍适应的控制方法。其核心是基于常规PID的控制基础建立预测自适应控制模型，实现对控制系统中温度的预测自适应PID调节。该方法将模型预测所得的未来一段时间内系统输出值与期望值的均方误差作为性能指标，以间接的方式动态调节PID参数，控制精度较高，充分发挥了PID方法的鲁棒性。所提方法实现了温度的精准控制，能够改善家禽的生活环境，实现高效的无人化管理环境，对于实际的家禽饲养提供参考。

　　关键词：温度控制；自适应PID；模型预测

　　0引言

　　目前，我国在家禽饲养方面大多还在延续比较传统的饲养方式。为满足市场的需求，各种大规模家禽饲养方式正在得到推广。由于家禽对环境的温度要求尤为苛刻，因此改善自动化温室控制系统显得尤为重要。

　　传统的PID算法有3个可调参数，应用广泛。但由于温度控制具有延迟和一定的非线性和滞后性，面对控制要求的不断提升，单纯依赖传统的PID已无法满足控制要求。近年来，有研究尝试将PID作为基础控制器，结合模糊PID、神经网络PID或蚁群等一些先进的算法去完成对温度的控制，均取得很好的控制效果。

　　随着自适应控制与预测控制方法的应用推广，面对复杂的控制对象（如时变、非线性、多变量等）更苛刻要求，结合PID控制方法的控制不足，预测控制、自适应控制与PID的三者结合得到了广大学者的高度关注。除此之外，专家还尝试将PID控制与其他先进理论相结合，很大程度上扩充了时变滞后系统的控制体系。

　　针对不同环境对温度的不同要求，本文提出了模型预测控制的自适应PID控制方法，其中包含系统模型建立，通过该模型得到预测的系统输出，以未来一段时间内预测的系统输出值与期望值之间的平方误差和最小原则指导PID控制器的参数变化。与其他模型的PID控制相比，本文模型预测指导的参数自适应，其控制精度较高，输出稳定，有易于实现和普遍适用的特点，可满足不同多种养殖生物的温度要求，实现智能高精度的温度控制。

　　1建立温度预测模型

　　环境温度直接影响家禽的生存状态。通过深入了解了家禽饲养环境中温度的变化的特性，通过预测模型与传统PID算法控制的结合，可以实时反馈未来时间的系统输出的大致基本状态。在建立预测模型时，可以针对未来若干个不同采样点的输出值作为反应目标，预测模型而不需要精准，省去了繁琐的理论求解过程。

　　1.1 PID控制法则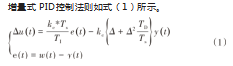

　　式中：u（t）、y（t）、w（t）分别为系统输入信号、输出信号和参考输入信号；Kc、TI和TD分别为比例增益、积分时间常数和微分时间常数，Ts为采样时间，Δ＝1-z-1为差分算子。

　　为了便于计算，可以令L（Z-1）=KC{Δ+Ts/Tl+Δ2 TD/Ts}。可以得出以下等式：

　　L（z-1）y（t）+Δu（t）-L（l）w（t）=0（2）

　　1.2预测控制法则

　　根据预测控制的基本原理，预测控制算法用二次型函数作为系统性能的指标：

　　J=(Yd--Yf)2+(Δ*U)2（3）

　　式中：Yd为期望输出的向量，不使用柔化方法时，可以使其作为设定值向量；为系统的未来输出自由响应估计向量，=Y（y（t），y（t-1），…，y（t-n1），Δ*u（t-1），Δ*u（t-2），…，Δ*u（t-m））；Yf为系统的未来输出强迫响应估计，Yf=Y（Δ*u（t），Δ*u（t+1），…，Δ*u（t+m2））；

　　Δ*u（t）为未来的待优化的控制向量。对J进行极小化分析，求得最优解：

　　Δ*u=P（Yd-0）（4）

　　对于Δ*u（t）、y（t）、yd（t）的相关算式。

　　P=[P1、P2、···Pn]=[1，0，0，···，0]*G，可以看出G是一矩阵组合，由0和Yf求得。

　　1.3预测模型建立

　　根据实际的家禽饲养环境，结合PID控制算法进行优化改进。

　　选用一阶系统的离散时域形式：

　　y（n）=Ay（n-1）+Bx（n）

　　式中：y（n）为系统第n个采样点的输出量，表示温度；A与B为比例系数；x（n）为第n个采样点的输入量。

　　一般情况下，温度控制系统中，加热装置和冷却装置对温控系统的影响比较大，其中热传导和热对流占比比较小，在大部分的情况下可以忽略不计。但是温控系统中温度存在滞后性，还有持续干扰等不确定性，可以采用以下预测模型：

　　y'（n）=Ay（n）+∑Bix（n-i）（5）

　　式中的y'（n）为模型预测系统中第n个采样点输出量，系数A和Bi为系统运行中实时反馈校正的系数。

　　根据Delta学习规则，先对该系统模型进行优化校正，可以得到如下等式：

　　A（n）=A（n-1）+ZAey（n）y（n-1）Bi（n）=Bi（n-1）+ZBiey（n）x（n-1）

　　ey（n）=y（n）-y'（n）（6）

　　式中：ey（n）为预测系统中输出与实际系统输出的偏差量；其中ZA、ZBi（i=1，2，…，τ）为系统模型反馈校正的学习速率，该参数可以根据后续的实际情况进行重新设定和选择适当的级别。

　　该建立的模型工作量相对较小，在采集临近时刻参数时还是相对比较准确的，可以满足实际的控制需求。

　　1.4控制器的建立

　　首先，选择位置式PID为基础控制器，公式为：

　　x（n）=KPe（n）+KIeI（n）+KDeD（n）（7）

　　式中：其中e（n）、eI（n）与eD（n）分别表示在第n个采样点控制系统输出的误差值、误差对时间的积分值与误差的微分值；KP、KI、KD分别为对应各部分的系数。将上式代入以上的预测模型：

　　y'（n）=Ay（n）+∑Bix（n-i）（8）

　　可得出根据历史数据预测未来一段时间中各个时刻对应的数据输出。将设定值设为Y，预测系统的偏差值表示为ef，可得出：

　　ef（n+j）=Y-y'（n+j）（9）

　　利用Delta学习规则，设定对PID的3个参数KP、KI、KD进行求偏导，求偏导过程与常规的自适应PID不一样，重新设定3个新的PID中间变量K、KI1、K，所以可得以下表达式：

　　K(n)=K(n-1)+ZP(-∂J(n)/∂KP)KI1(n)=KI1(n-1)+ZI(-∂J(n)/∂KI)

　　K(n)=K(n-1)+ZD(-∂J(n)/∂KD)（10）

　　式中：ZP、ZI、ZD均表示预测模型中的学习参数，通过式（10）与基础的位置式PID表达式可以整理化简为：

　　KP(n)=KK(n)/(|KP(n)|+|KI1(n)|+|K(n)|)

　　KI(n)=KKI1(n)/(|KP(n)|+|KI1(n)|+|K(n)|)

　　KD(n)=KK(n)/(|KP(n)|+|KI1(n)|+|K(n)|)（11）

　　式中：K为比例系数，其值是对整个预测模型的初始值，PID的对应系数需要根据实际情况选择设定。

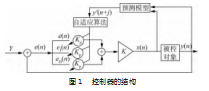
　　综上分析可得，在预测自适应模型中需要考虑4个参数，分别为K、KP、KI、KD，并没有因选用了自适应预测模型增加过多的参数，保留PID的控制优势。控制器的结构如图1所示。

　　2工业控制系统设计

　　2.1系统硬件设计

　　PLC作为比较常用的工业控制器，本文选用的S7-200 SMART PLC作为控制，CPU型号为SR40，加热器和制冷风扇作为控制系统中的被控对象。

　　在控制系统中，被控对象采用1个半封闭式的箱体，半封闭的容器内放置了1个液体容器，箱体内部的温度可以通过改变内部的液体利用控制器上的温度采集模块进行温度的数据采集，输出控制信号分别控制加热装置和制冷装置；热电偶的作用是采集温度的实时数据；最后通过上位监控系统实现对数据进行读取。控制系统的结构如图2所示。

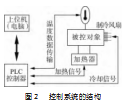
　　被控对象中的温度加热至100℃需15 min左右，被控对象中的装有制冷风扇和热电偶，可以对箱体的温度进行降温，若箱体内温度需要降温可启动制冷风扇，需要升温时可开启热电偶。

　　控制器的设置为：频率为1 Hz，系统输出为-1 000~1 000之间。

　　2.2系统软件设计

　　控制系统PLC编程软件为STEP 7-MicroWIN SMART，上位机组态软件为Kingview（组态王）。控制系统中温度通过温度采集模块和热电偶获取，PLC编程软件实现对加热器和制冷风扇的控制，使用Kingview组态软件绘制监控界面实现对控制系统监控作用。

　　Kingview组态软件监控界面的建立步骤如下：

　　（1）新建工程；（2）绘制监控界面；（3）数据词典中新建IO变量和内存变量；（4）监控界面中的图素和变量之间的动画链接；（5）编写监控界面的命令语言；（6）组态软件与硬件之间进行监控运行。通过以上操作步骤完成上位机监控界面的设计。

　　针对控制系统的运行，使用普通PID的控制方法与预测模型中的自适应PID控制方法进行比较，比较两种方法的控制效果。

　　通过经验试凑法，先确定PID中KP=30，KI=1，KD=10，将3个参数作为普通控制下的设定参数；在有预测模型中自适应算法中，将控制的4个参数选取K=0.1、KP=30，KI=1，KD=10。利用以上两种设定参数对不同温度下的数据进行记录。

　　3系统测试实验与效果分析

　　控制系统中选取50℃与60℃两种设定值在不同时刻情况的数据进行记录，被控对象在有无自适应算法的两种情况下对数据进行记录，针对不同时刻记录下的一系列数据进行温度走势的曲线绘制，绘制的控制曲线如图3~4所示。

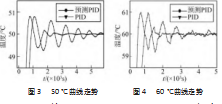
　　根据以上绘制的控制曲线走势，可以得出对应每一种控制曲线下的上升时间、温度的调节时间、最大动态偏差值、稳态误差值，具体的控制效果数据如表1所示。

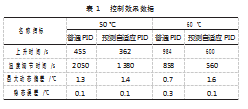
　　由表中控制指标数据可得，在50℃与60℃两种不同设定温度下，本文模型提高温度达到设定温度的时间较短；受到扰动时，普通PID需要的调节时间要比预测自适应PID的调节时间长；最大动态偏差与稳态误差在预测自适应PID的控制下相对比较稳定，控制效果要好于普通PID控制。

　　通过以上两个不同温度的控制效果，在有预测自适应模型的优化下，温度的控制响应速度和控制稳定性能较快地进入平稳状态。

　　结果表明，预测模型自适应PID对温度的控制响应时间比普通的PID控制时间要短，缩短了温度的响应时间，同时提高了控制精度，能最大化地提升对温度的控制效果，减少温度的不稳定对家禽生存的影响，提高家禽的存活率。

　　4结束语

　　本系统设计基于在家禽的饲养环境中，鉴于温度的控制存在很大的滞后性，响应速度相对比较慢，温度对家禽的生存环境起着至关重要的作用，针对家禽环境中温度进行控制，基于传统的PID控制算法，结合一阶系统的离散时域形式，建立了预测模型，模型中将自适应算法与PID控制配合调节温度控制，在不同的温度设定值前提下，将自适应的PID控制算法与传统的PID控制算法对不同温度进行了控制结果的分析，得出预测模型在自适应PID算法的基础上温度的控制效果在时间响应上明显高于普通的PID温度控制系统，在调节时间和系统稳态误差上对温度的控制响应和收敛性都比较好，提升了家禽饲养环境中温度的控制效果，对实际家禽饲养中有很好的参考价值。

      参考文献：

　　[1]姚顺峰.温湿度对鸡饲养管理的重要性[J].当代畜禽养殖业,2020(2):10-11.

　　[2]麻丽明,何应良,谷子中,等.基于MCGS家禽饲养温控系统的设计与开发[J].机电工程技术,2022,51(11):134-137.

　　[3]冯程程,龚希武,刘要.蔬菜大棚温度自动控制系统设计[J].安徽农业科学,2017,45(22):171-173.

　　[4]唐华兴.吹塑机温度智能实时控制系统研究与设计[J].装备制造技术,2023,(01):207-209,228.

　　[5]刘艳君,毛亚文.一类基于预测的自适应PID控制器[J].系统仿真学报,2015,27(11):2778-2783,2790.

　　[6]董伟鹤,国亮.基于预测控制的自适应PID控制器设计与仿真[J].电子技术,2009,36(9):22-24.

　　[7]孙艳萍,黄东安.基于广义预测控制的自适应PID电厂主温度控制仿真研究[J].科技信息,2009(35):1201,1193.

　　[8]王江荣.基于灰色广义预测模型的自适应PID控制算法[J].电气自动化,2013,35(1):12-13,106.

　　[9]宿刚,刘浩,乔君丰,等.适用于温度系统的预测自适应PID控制方法[J].吉林大学学报(信息科学版),2022,40(1):1-6.

　　[10]姚立平,吴文明,姜杨阳,等.一种引入不完全微分PID控制算法在温控系统中的应用[J].科技创新与应用,2022,12(19):8-12,17.

　　[11]李兵,范莉惠.灰色预测模糊自适应PID控制在供热系统中的应用[J].唐山学院学报,2015,28(3):18-20.

　　[12]张立优,马珺,贾华宇,等.基于在线序贯极限学习机的温室温度预测方法及其自适应控制系统设计[J].江苏农业科学,2018,46(14):226-230.

　　[13]李宁,尚雯珂.基于分布式温度传感的在线学习自适应模糊温度预测法[J].电气传动自动化,2022,44(4):52-57.

　　[14]谢七月,周超.基于改进自适应GPC的锅炉主蒸汽温度预测控制[J].热能动力工程,2018,33(12):86-92.

　　[15]向晓汉.S7-200 SMART PLC完全精通教程[M].北京:机械工业出版社,2013.

　　[16]麻丽明,赵海志,殷忠敏.基于组态王小型生产线监控系统的设计与开发[J].机电工程技术,2022,51(3):207-210.

　　[17]胡冬雪,张宗达,王睿,等.基于新型模糊PID算法的恒温控制系统研究[J].吉林大学学报(信息科学版),2018,36(3):312-317.

　　[18]凡占稳,单琼飞,尹承锟,等.基于单神经元PID的真空炉自适应温度控制[J].金属热处理,2020,45(12):237-241.