摘要：针对五轴数控机床在加工过程产生的多类别融合误差影响着机床加工精度的问题，提出一种基于误差耦合的综合误差模型建立方法。从误差源的角度出发，分析影响机床加工精度的主要因素，探究不同误差对机床加工精度的影响。在此基础上建立了目标机床的拓扑结构和低序体阵列，从而完成了基于多体系统理论的理想状态和实际状态下的综合误差齐次坐标变换矩阵的推导，由此建立起目标机床的综合误差模型，并给出了综合误差模型正确性的验证。提出了一种先插值后拟合方法对五轴数控机床误差进行拟合。实验结果表明，该方法可有效地处理误差波动较大的数据，相较而言，拟合偏差降低了3.04%，提高了五轴数控机床综合误差模型精度。

      关键词：五轴数控机床；多体系统；误差拟合；综合误差模型

　　0引言

　　五轴数控机床被广泛应用于工业领域的高端精密装备。其作业的高精度要求使其成为研究热点。一般提高机床加工精度的途径是对机床误差进行补偿，而补偿精准与否，取决于机床加工时误差辨别的精准度。为此，机床作业时的误差建模方法一直备受关注。

　　从误差源表征特性分析，数控机床误差建模大致分为几何误差建模、力误差建模、热误差建模三类，在机床众多原始误差类别中，几何误差是影响最大的。尽管针对数控机床的误差建模研究有着瞩目的成果，但就现在的技术而言，机床加工精度与所产生的误差之间的关系仍未能采用单一模型完美地体现。

　　针对不同误差源的分析，已证明了不少模型是可行的。而单一误差建模分析往往会由于其他误差源的影响而造成拟合精准度不高，因此建立统一的、综合的误差模型会有更高的通用性和灵敏性[。特别地，吴剑波针对大型龙门自动铺丝机（AFP）提出重力变形与几何误差综合建模与补偿方法，实验表明经补偿后的位置误差降低了90%，位姿误差降低了80%。为研究精密数控机床的加工精度，王伟文[19]提出面向四轴抛光平台的几何与热的综合误差建模方法，采用切比雪夫与最小二乘法对误差进行拟合，该方法建立的模型确实具有强预测性和鲁棒性，但由于最小二乘法拟合并不要求拟合函数经过样本点，只要求总体误差最小，导致该方法只适合拟合呈线性分布的误差。

　　综上，精密数控机床的综合误差建模取得了阶段性进展，但模型精度有待进一步提高。另外针对高精五轴龙门数控加工中心的综合误差分析寥寥无几，为此本文基于多体系统理论，开展高精五轴龙门数控加工中心的综合误差建模研究。提出一种基于误差耦合的综合误差模型建立方法。具体而言，基于多体系统理论分析理想状态和实际状态的综合误差齐次坐标变换状态，并由此建立起目标机床的综合误差模型，且给出了综合误差模型正确性的验证，最后提出一种先插值后拟合方法，完成对五轴数控机床误差的拟合。

　　1综合误差建模

　　由于多种因素影响着五轴数控机床的误差，给研究带来了复杂的运算，甚至难以得到其准确的结果，所以本文对同一位置的误差进行相互耦合，例如：机床沿X轴的定位误差δxX受到几何误差（g），热变形误差（t），力变形误差（f）三个因素的影响，现整合成一个误差为δxX（g，t，f）。其他误差整合如表1所示。

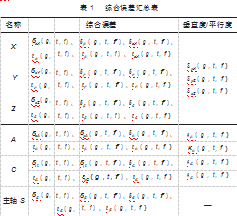
　　1.1目标机床拓扑结构与低序体阵列

　　机床误差最直接的反映就是待加工工件与刀具相对位置的偏移量。目标机床结构如图1所示，机床各坐标轴的正方向的误差是正误差，根据右手螺旋定理决定转角误差的正负。机床的拓扑结构如图2所示，床身、A轴、C轴、工件、Y、X、Z轴、S主轴、刀具相对应的坐标系编号依次为0、1、2、3、4、5、6、7、8，其中A、C轴为旋转轴，X、Y、Z轴为移动轴。目标机床的低序体阵列如表2所示。

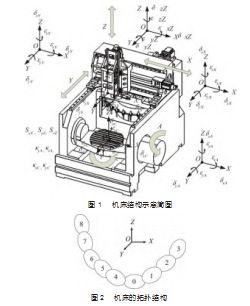
　　1.2理想状态综合误差齐次坐标变换

　　对目标机床进行分析时，假设3个移动轴分别移动x距离，y距离和z距离；两个旋转轴分别旋转a角度和c角度，因此可以通过齐次变换来求出工件到刀具的误差变化分量。另外，为了简化计算量，若相邻序体无明显的相对位移，假设它们之间的变换矩阵为单位矩阵。现在进行理想状态下机床各轴的齐次坐标变换矩阵推导。可以得出在理想状态下，目标机床从工件到刀具的齐次坐标变换矩阵为：

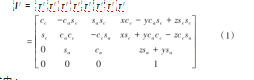
　　式中：

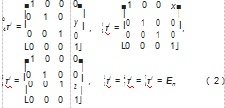
　　从工件链分析，τi、τi、τi、τi、τi分别为从A轴到床身的变换矩阵、从C轴到A轴的变换矩阵、从工件到C轴的变换矩阵；从刀具链分析，τi、τi、τi、τi、τi分别是从床身到Y轴的变换矩阵、从Y轴到X轴的变换矩阵、从X轴到Z轴的变换矩阵、从Z轴到S主轴和从S主轴到刀具的变换矩阵。

　　1.3实际状态综合误差齐次坐标变换

　　为改善模型的复杂性，简化运算量，把几何、热、力等3个因素作用的9个移动误差整合成3个移动误差，分别为δxY（g，t，f）、δyY（g，t，f）、δzY（g，t，f）。转角误差仍为εyY（g）、εxY（g）、εzY（g）。根据最小误差假设理论得到实际床身到Y轴的变换矩阵τe、实际从Y轴到X轴的变换矩阵τe、实际从X轴到Z轴的变换矩阵τe、实际从A轴到床身的变换矩阵τe、实际从C轴到A轴的变换矩阵τe、从工件到C轴τe，从Z轴到S主轴τe、从S主轴到刀具的变换矩阵τe，具体如下：

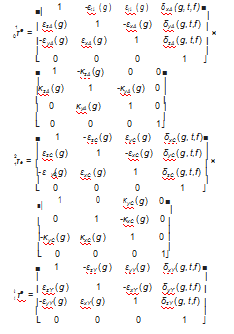
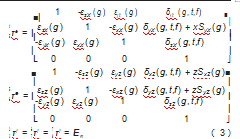
　　由式（3）可以得出，在实际状态下，目标机床从工件到刀具的齐次坐标变换矩阵为：

　　τ=τiτeτiτeτiτeτiτeτiτeτiτeτiτeτiτe（4）

　　根据小误差假设理论，误差变换矩阵等于实际状态下的齐次坐标变换矩阵减去理想状态下的齐次坐标变换矩阵。即E=τ-I，则有

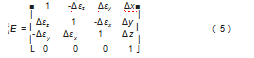
　　根据最小误差理论，且不考虑二阶及二阶以上小量，得出五轴数控机床实际加工的各误差分量：

　　Δx=cc[-δxC(g,t,f)-yεzC(g)-yκzA(g)]+sc[-δyA(g,t,f)-δyC(g,t,f)+

　　δyX(g,t,f)-δyY(g,t,f)+δyZ(g,t,f)-

　　yεzC(g)-xεzA(g)-xεzY(g)+zεxB(g)-zεxX(g)+zεxY(g)-xκyC(g)-xSyX(g)-zSyZ(g)]-zκyC(g)ca+cc c a[-δxB(g,t,f)+δxX(g,t,f)-δxY(g,t,f)+δxZ(g,t,f)]+

　　Cc C a[δxC(g,t,f)-δzX(g,t,f)+

　　δzY(g,t,f)-δzZ(g,t,f)-xεzC(g)-

　　xεzA(g)-xεzY(g)]+ca cc[-xεzC(g)-zSxZ(g)-

　　yεxA(g)+zεxC(g)-xκzA(g)+zκzA(g)]+

　　S c Sa[xεxC(g)+zεzC(g)+xκyA(g)+zκyA(g)]  （6）

　　Δy=cc[-δyA(g,t,f)-δyC(g,t,f)+

　　δyX(g,t,f)-δyY(g,t,f)+δyZ(g,t,f)-

　　xεzA(g)-xεzY(g)+zεxA(g)-zεxX(g)+

　　zεxY(g)-xSyX(g)-zSyZ(g)]+zκxC(g)ca+

　　sc[δxC(g,t,f)+yεzC(g)+yκyA(g)]+

　　xκxC(g)s a+sc sa[δyA(g,t,f)-δxX(g,t,f)+δxY(g,t,f)-δxZ(g,t,f)+zSxZ(g,t,f)]+s c sa[δzA(g,t,f)+δzX(g,t,f)-δzY(g,t,f)+δzZ(g,t,f)]+ca sc[yεzA(g)+zεyA(g)+

　　zεzC(g)-zεyX(g+zεyY(g)]+cc s a[zεzC(g)+

　　xκyA(g)+zκzA(g)+xεxC(g)+s c sa[xεyA(g)+

　　xεyC(g)+xεyY(g)+yεyA(g)]（7）

　　Δz=δzC(g,t,f)+y[εxC(g)+κyA(g)]+ca×

　　[-δzA(g,t,f)+δzX(g,t,f)-δzY(g,t,f)+

　　yεxA(g)δzZ(g)+xεyA(g)+xεy C(g)+

　　xεyY(g)+yεyA(g)]+s a[-δxA(g,t,f)+

　　δxX(g,t,f)δxY(g,t,f)+δxZ(g,t,f)-

　　yεzA(g)-zεyA(g)-zεyC(g)+zεyX(g)-

　　zεyY(g)]-zSxZ(g)+yκxC(g)cc-

　　yκyC(g)sc+xκyC(g)cc c a+xκxC(g)sc ca-

　　zκyC(g)s a cc-zκxC(g)sc sa（8）

　　Δεx=-κyA(g)-εxC(g)+cos(a)[-εxA(g)+

　　εxX(g)-εxY(g)+εxZ(g)]-cos(c)×

　　κxC(g)+sin(a)[εzA(g)-εxX(g)+

　　εxY(g)-εxZ(g)]+sin(c)κyC(g)（9）

　　Δεy=-εyC(g)ca+sc[εxA(g)-εxX(g)+εxY(g)-εxZ(g)]+ca cc[-εyA(g)-εyC(g)+

　　εyX(g)-εyY(g)+εyZ(g)]+ca cc[εxC(g)+

　　κyA(g)]+sa sc[κzA(g)+εzC(g)]（10）

　　Δεz=cc(εzX(g)-εzA(g)-εzY(g)+εzZ(g))+

　　s aκxC(g)+ca cc[-εzC(g)-κzA(g)]+

　　cc s a(εxC(g)+κyA(g))+sa sc(εyA(g)+

　　εyC(g)-εyX(g)+εyY(g)-εyZ(g))（11）

　　2综合误差模型正确性分析

　　由于所建立的五轴数控机床的综合误差模型受多种因素影响，很难直接对其整体的正确性进行验证，因此本文为不失一般性地分析五轴数控机床综合误差模型正确性，设定以下条件：A轴的旋转角度a和C轴旋转的旋转角度c足够小，且忽略热变形误差与力变形误差，省略二阶及二阶以上小量，根据式（5）得出特殊状态下的齐次变换矩阵为：

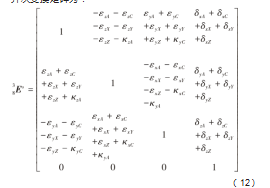
　　各误差分量为：

　　Δx=δxA+δxC+δxX+δxY+δxZΔy=δyA+δyC+δyX+δyY+δyZΔz=δzA+δzC+δzX+δzY+δzZ

　　Δεx=εxA+εxC+εxX+εxY+εxZ+κxC+κyAΔεy=εyA+εyC+εyX+εyY+εyZ+κyC

　　Δεz=εzA+εzC+εzX+εzY+εzZ+κzA（13）

　　将式（13）与式（6）~（11）进行对比，结果相一致，从而验证了五轴数控机床综合误差模型的正确性。

　　3误差辨识与验证

　　在不失一般性的前提下，本节误差模型仅探究移动轴，旋转轴暂不探究。即A轴与C轴不处于工作状态。五轴数控机床X轴几何误差数据来源文献。

　　本文结合最小二乘法与三次样条插值法，针对变化波动较大的误差提出了先三次样条插值，再最小二乘法拟合的策略。仿真结果如图3~5所示。此外为验证所提方法的性能优越性，对X移动轴Z向直线度误差进行拟合时将所提方法与最小二乘法进行对比，对比结果如图6所示。

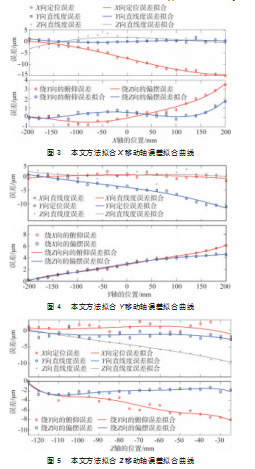
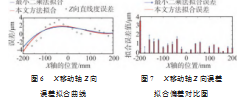
　　从图3可以得出，用最小二乘法拟合出来的结果并不理想。这是因为最小二乘法拟合并不要求拟合函数经过样本点，只要求总体误差最小，所以十分适合拟合一些呈线性分布或者变化波动较小的误差。但是，当拟合变化波动较大的误差时，拟合出来的曲线精准度会有所下降。相较之下，在图7和表3中可知本文所提先插值后拟合的方法拟合出来的曲线均更能逼近原始数据，具体而言，本文所提出方法的拟合误差相较最小二乘法降低了3.04%。此外，由图3~5可见，在各轴误差拟合方面，本文所提先插值后拟合的方法拟合出来的曲线均能逼近原始数据。
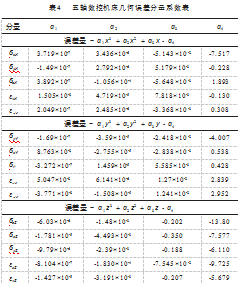
     利用MATLAB计算得出五轴数控机床几何误差分量，结果如表4所示。

　　4结束语

　　本文针对五轴数控机床在加工过程产生的多类别融合误差影响着机床加工精度的问题，提出了一种基于误差耦合的综合误差模型建立与误差拟合的方法。具体而言，首先建立了目标机床的拓扑结构和低序体阵列，在此基础上运用多体系统理论对理想状态和实际状态下的综合误差进行齐次坐标变换推导，由此建立起目标机床的综合误差模型，并验证了综合误差模型的正确性。最后本文提出的先插值后拟合的方法，实验结果表明，该方法可有效地处理误差波动较大的数据，相较最小二乘法而言，拟合偏差降低了3.04%，因而拟合精度得到了提高。

　   参考文献：

　　[1]李高强,张宇,李鸣.基于GA-LSSVM的数控机床热误差建模方法研究[J].机床与液压,2021,49(2):26-30.

　　[2]王艳红,喻伟男,李冬,等.五轴数控机床非线性误差建模及补偿方法[J].组合机床与自动化加工技术,2022(2):25-28.

　　[3]NI Y,JIA S,ZHANG Z,et al.A manufacturing-oriented error modelling method for a hybrid machine tool based on the 3-P RS parallel spindle head[J].Advances in Mechanical Engineering,2019,11(5):168-181.

　　[4]LYU Dun,LIU Qing,LIU Hui,et al.Dynamic error of CNC machine tools:a state-of-the-art review[J].The International Journal of Advanced Manufacturing Technology,2020,106(5/8):1869-1891.

　　[5]李海洲,谢丽军,周梦洁,等.进给系统机电耦合仿真建模与误差影响规律分析[J].机电工程技术,2023,52(12):154-158.

　　[6]TAN Zhou,LIAO Yinghua,JIANG Jie,et al.A method of sensi‐tivity analysis and precision prediction for geometric errors of five-axis machine tools based on multi-body system theory[J].The International Journal of Advanced Manufacturing Technolo‐gy,2022,123(9-10):3497-3512.

　　[7]宋占群.可重构数控机床几何误差高效建模与敏感性研究[D].扬州:扬州大学,2022.

　　[8]ZHANG C J,LIU H L,ZHOU Q L,et al.A support vector re‐gression-based method for modeling geometric errors in CNC machine tools[J].The International Journal of Advanced Manu‐facturing Technology,2023,131(5-6):2691-2705.

　　[9]LEETE DL.Automatic compensation of alignment errors in ma‐chine tools[J].International Journal of Machine Tool Design and Research,1961,1(4):293-324.

　　[10]魏丽霞,李向丽,张勇.基于支持向量机算法的数控机床切削力误差实时补偿[J].机械制造与自动化,2016,45(5):58-60,86.

　　[11]刘焕牢,苏妙静,刘璨,等.数控机床切削力误差研究方法探讨[J].制造技术与机床,2020(8):58-62.

　　[12]宋飞虎,王梦柯,尹静,等.基于数字孪生控制的精密机床热误差模型[J].机电工程,2023,40(3):391-398.

　　[13]杜柳青,余永维.基于序列深度学习的数控机床热误差建模与预测方法[J].机床与液压,2020,48(23):88-92.

　　[14]白路,罗忠辉,阮毅,等.数控立式加工中心主轴热变形测试与建模研究[J].机电工程技术,2019,48(10):57-59.

　　[15]王子涵,杨秀芝,段现银,等.基于贝叶斯神经网络的机床热误差建模[J].制造技术与机床,2022(1):141-145.

　　[16]刘九庆,金雨飞,丁禹程,等.MXK3120单端铣机床加工工艺参数综合误差模型的构建及对铣削主轴结构参数的优化[J].东北林业大学学报,2022,50(2):93-99.

　　[17]牛亚军.数控机床加工过程综合误差分析[J].现代农机,2020(5):58-59.

　　[18]吴剑波,李俊,郑成淦,等.大型龙门铺丝机综合误差建模及补偿[J].浙江大学学报(工学版),2022,56(2):398-407.

　　[19]王伟文.精密多轴数控机床误差建模研究[D].长春:长春工业大学,2020.

　　[20]程亚平.多轴精密数控机床误差测量与建模研究[D].长春:长春工业大学,2018.