摘要：随着列车速度的进一步提高，轨道激扰对车体振动的影响也更为明显。因此，在高速运行时，列车更容易受到制动系统动态特性的影响，对车辆运行的安全性构成威胁。为了研究车辆振动对高速列车制动系统力承载边界的影响，首先建立了具备制动系统的高速列车整车动力学模型，并进行了仿真计算。其次，研究了制动初速度、减速度、轴重以及线路不平顺幅值对制动盘压力波动的影响。研究结果表明，受到线路激扰的影响，位于轮对上的制动盘与位于转向架构架上的制动夹钳之间产生相对振动，导致制动压力在额定压力附近波动（约为±5%）。此外，制动初速度和线路不平顺的增大、减速度的降低均会加大制动压力的波动。因此，在分析评估高速列车制动系统温度和振动特性时，特别是在高干扰线路条件下，需要考虑车辆振动环境的影响。

　　关键词：高速列车,制动系统,动力学,轨道不平顺

　　0引言

　　近年来，高速铁路因其安全性高、速度快、运营时刻准等特点，成为了人们日常生活中被广泛接受的交通方式。随着列车速度的不断提高，对制动的安全性和可靠性的要求更为严苛。面向“十四五”规划，聚焦国家战略亟需，对高速列车进一步提速提出要求。速度要提高至450 km/h，既对轻量化提出了要求，又对制动性能的要求更高。然而由于轨道激扰等因素，高速列车在制动时极易产生制动盘磨损，缩短服役寿命[1-2]，甚至还会产生严重的噪声，影响司机及乘客乘坐舒适性并且可能会对乘客相关人员的身心健康造成潜在危害[3]。此外，由于制动盘是安装在车轴上的，因此轨道激扰对车体产生的影响也会直接作用在轮盘上，这会导致高速列车在运行时极易受到制动系统动态性的影响，从而对车辆运行的安全性构成威胁[4]。

　　张天成[5]从材料的自身特性出发，研究制动盘的温度特性与疲劳损伤。唐斌等[6]考虑到沙区铁路制动盘的磨损，从沙粒特性角度出发，研究不同的沙粒对于制动盘表面磨损的演变过程。项载毓等[7]从结构出发，设计了一种三明治阻尼结构降低制动块摩擦时的表面接触，改善摩擦块的摩擦磨损特性，从而减少制动系统动态性对高速列车运行产生的影响，提高列车运行的安全性。Waddad等[8]考虑到制动界面粗糙度的影响，在此基础上对制动盘进行仿真，获得了考虑粗糙度的制动盘温度场分布规律。丁思源等[9]从温度出发，研究不同低温影响下高速列车制动盘材料的力学性能，分析其对于制动盘疲劳裂纹扩展速率的影响。孙洪雨等[10]在4种不同温度梯度下研究高速列车制动盘的磨损行为。童欣[11]则是研究了一种纳米级相变储热材料，以满足长大坡道线路对于制动盘的高效散热要求。喻亮等[12]也建立了一种带有三维网络碳化硅骨架增强铝基复合材料的制动盘，并研究了制动初速度380 km/h下的温度变化情况。周素霞等[13]设计了3种不同散热筋结构的制动盘，并对其进行热力耦合研究。张英才[14]也从散热筋的尺寸参数与位置参数出发，采用4因素正交实验方法，研究得到具有最佳散热性能时的制动盘结构参数。吕雪梅等[15]从接触热阻的角度研究制动盘的热机耦合行为。此外，当研究制动系统时，研究人员通常会采用如数值模拟、缩比试验和全尺寸试验等方法来研究其摩擦震颤、制动噪声及其他特性[16-18]。范志勇等[19]发现由于闸片制动时表面会由于受力不均，闸片的摩擦粒子会产生过度磨损、偏磨等现象，从优化摩擦粒子的角度出发，改善高速列车运行的安全性。陈有洁[20]也从材料特性出发，开展树脂基合成材料、半金属基合成材料及铜基粉末冶金材料与锻钢制动盘配副的对比试验，探究不同材料对制动盘最高温度的差异。吴元科[21]、项载毓[22]等均研究了闸片摩擦块的不同结构、数量及排布对于制动盘摩擦特性的影响。以上虽然对制动系统都进行了深入的研究，但是忽略了不同制动特性与外界激扰对于制动系统力承载边界的影响。事实上，尤其是在高速运行下，不同制动特性与外界激扰对于制动盘的震颤、噪声以及温度特性都有着重要的影响[23-24]。因此，研究不同制动特性与外界激扰下的制动盘力承载边界是非常重要的。

　　基于以上问题，本文建立了高速列车整车动力学模型，并考虑了制动系统服役过程中的车辆振动环境。基于建立的模型，研究了制动盘的力承载边界，为后续开展车辆振动环境下高速列车制动系统的温度和振动特性研究提供了理论依据。

　　1高速列车动力学模型

　　1.1仿真计算模型

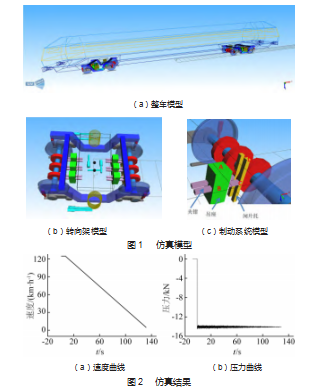
　　建立标准动车组车辆动力学模型和制动系统（图1（a）），每根车轴设置3个制动轴盘并跟随车轴转动（图1（b）），制动系统如图1（c）所示。单个制动系统包括1个吊座，左右2个夹钳，左右两个闸片托（闸片与闸片托固结为一体），1个制动盘。其中，吊座于A点通过橡胶套筒与转向架连接，左右夹钳于B点绕Z轴旋转与吊座连接，闸片托于C点沿着Z轴平动与夹钳连接，并在D点通过垂向弹簧与转向架连接。制动时，左右闸片托夹紧制动盘，产生正压力和摩擦力，摩擦因数设置为0.33。

　　模型采用套管模拟橡胶的各向刚度，各项刚度值为：轴向刚度500 N/mm；径向刚度5 000 N/mm；扭转刚度5 000 N·m/(°);偏转刚度25 000 N·m/(°)[25]。

　　1.2仿真计算

　　设定以下工况：车辆在直线线路运行，初始运行速度450 km/h，仿真计算时间132 s，从7 s后施加德国低干扰谱。此外，车辆在7 s时刻开始制动减速，减速度为1 m/s2。

　　仿真结果如图2所示。从图2（a）中可以看出，列车在7 s时刻在制动力的作用下按照设计的1 m/s2的减速度从初始速度450 km/h开始均减速运动，表明制动力已成功施加在车辆模型上。此外，由于线路激扰的影响，导致位于转向架构架的制动夹钳与位于车轴上的制动盘之间发生横向相对位移。车辆制动过程中，由于制动盘与夹钳的横向位移，导致同一制动盘左右两侧的制动压力发生波动（图2（b））。除此以外，从图2（b）中可以看出，制动压力随着车辆速度的降低而逐渐降低。

　　2不同制动工况下的制动盘力承载边界

　　2.1工况参数设置

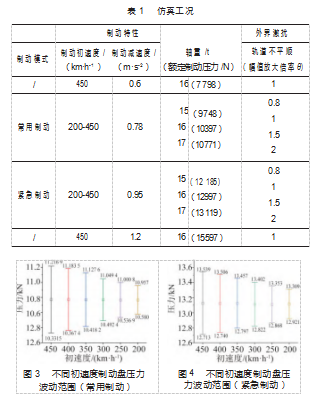
　　基于标准动车组车辆动力学模型，对列车常用制动工况与紧急制动工况进行仿真计算，分别研究制动初速度、减速度、轴重以及轨道不平顺、车轮磨损、制动盘偏磨等多种因素对碳陶制动盘力承载边界的影响。针对每一种参数设定多个取值，利用动力学仿真模型对设定工况进行仿真分析，提取制动过程中的压力波动范围，为后续探讨力承载边界变化对碳陶制动盘的影响提供研究基础。本文涉及的所有工况汇总如表1所示。

　　2.2制动初速度变化对制动盘力承载边界的影响

　　本节主要研究制动初速度对制动盘力承载边界的影响规律。将列车轴重设置为17 t，制动减速度为0.78 m/s2（常用制动）与0.95 m/s2（紧急制动），制动初速度分别设置450、400、350、300、250、200 km/h，继而对不同列车制动初速度进行仿真计算，可得到不同制动初速度下制动盘压力波动，仿真结果如图3~4所示。

　　对于紧急制动，从压力值角度分析，当制动初速度为200 km/h时，制动盘最大压力约为13 309 N，此后速度每提升50 km/h，压力大约提升50 N，速度基数越高，压力提升值越大，当制动初速度为450 km/h时，制动盘最大压力约为13 539 N。对于常用制动，从压力值角度分析，当制动初速度为200 km/h时，制动盘最大压力约为10 957 N，此后速度每提升50 km/h，压力大约提升60 N，速度基数越高，压力提升值越大，当制动初速度为450 km/h时，制动盘最大压力约为11 217 N。

　　为了更直观地对制动盘力承载边界进行对比分析，分别以制动初速度为横坐标、压力偏差百分比为纵坐标，画出不同制动初速度下制动盘压力偏差百分比曲线，如图5~6所示。

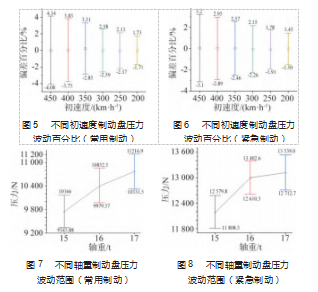
　　分析上图可得，不论是常用制动还是紧急制动，制动初速度越大，压力波动就越大。初速度为450 km/h时，常用制动压力波动为-4.08%~4.14%；紧急制动压力波动为3.1%~3.20%。

　　2.3轴重变化对制动盘力承载边界的影响

　　本节主要研究轴重对制动盘力承载边界的影响规律。将列车初速度设置为450 km/h，制动减速度为0.78 m/s2（常用制动）与0.95 m/s2（紧急制动），轴重分别设置为15、16、17 t，继而对不同列车制动初速度进行仿真计算，可得到不同轴重下制动盘压力波动，仿真结果如图7~8所示。

　　对于紧急制动，从压力值角度分析，当轴重为15 t时，制动盘最大压力约为12 580 N，轴重基数越高，压力提升值越大，当制动初速度为17 t时，制动盘最大压力约为13 539 N。对于常用制动，从压力值角度分析，当轴重为15 t时，制动盘最大压力约为10 166 N，轴重基数越高，压力提升值越大，当轴重为17 t时，制动盘最大压力约为11 217 N。

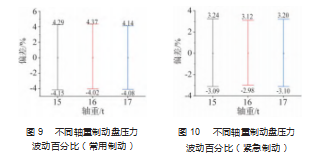
　　与上节类似，分别以轴重为横坐标、压力偏差百分比为纵坐标，画出不同轴重下制动盘压力偏差百分比曲线，如图9~10所示。

　　从图中可以看出，当轴重为15 t时，常用制动压力偏差百分比为-4.15%~4.29%，紧急制动压力偏差百分比为-3.09%~3.24%；当轴重为17 t时，常用制动压力偏差百分比为-4.08%~4.14%，紧急制动压力偏差百分比为-3.10%~3.20%，二者相比制动压力偏差百分比误差不大。这是因为，不论是常用制动还是紧急制动，随着轴重增加，压力偏差值也随之增大；但由于轴重增加的同时伴随着额定制动压力的增加，因此计算得到的压力偏差百分比值并没有随着轴重增大而增大。

　　2.4制动减速度变化对制动盘力承载边界的影响

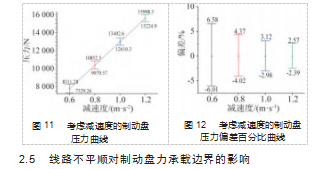
　　本节主要研究制动减速度对制动盘力承载边界的影响规律。将列车初速度设置为450 km/h，制动减速度为0.6、0.8、1.0、1.2 m/s2，轴重为16 t，继而对不同列车制动减速度进行仿真计算，可得到不同制动减速度下制动盘压力波动，仿真结果如图11所示。

　　从压力值角度分析，当制动减速度为0.6 m/s2时，制动盘最大压力约为8 311 N，伴随着减速度提高，压力提升值也随之增大，当制动减速度为1.2 m/s2时，制动盘最大压力约为15 998 N。

　　同样，分别以减速度为横坐标、压力偏差百分比为纵坐标，画出不同制动减速度下制动盘压力偏差百分比曲线，如图12所示。从图中可以看出，当制动减速度为0.6 m/s2时，压力偏差最大为513.28 N，此时的偏差百分比达到6.58%；当制动减速度为1.2 m/s2时，压力偏差最大为401.3 N，此时的偏差百分比达到2.57%。因此，不难看出，随着减速度增加，压力偏差值和压力偏差百分比都随之降低。这是因为，随着制动减速度增加，额定制动压力也随之增加，这也意味着此时制动盘被夹得越紧，这时的压力偏差值也会因为制动盘晃动减小而变小。

　　2.5线路不平顺对制动盘力承载边界的影响

　　本节主要研究线路不平顺对制动盘力承载边界的影响规律。由于仿真选用德国低干扰谱，考虑线路磨损的不同，本节将幅值相应缩放0.8~2倍。因此具体仿真工况如下：选取初速度450 km/h，制动减速度为0.78 m/s2（常用制动）与0.95 m/s2（紧急制动），轴重为17 t，线路谱幅值放大倍率θ分别为0.8、1、1.5、2。继而对不同线路不平顺幅值进行仿真计算，可得到不同线路不平顺幅值下的制动盘压力波动，仿真结果如图13~14所示。

　　对于紧急制动，从压力值角度分析，当线路谱幅值放大倍率θ为0.8时，制动盘最大压力约为13 489 N，伴随着线路谱幅值放大倍率θ提高，压力提升值也随之增大，当线路谱幅值放大倍率θ为1.2时，制动盘最大压力约为13 768 N；对于常用制动，从压力值角度分析，当线路谱幅值放大倍率θ为0.8时，制动盘最大压力约为11 164 N，伴随着线路谱幅值放大倍率θ提高，压力提升值也随之增大，当线路谱幅值放大倍率θ为1.2时，制动盘最大压力约为11 478 N。

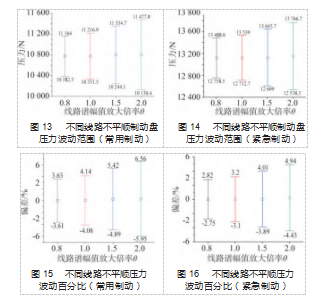
　　分别以线路谱幅值放大倍率θ为横坐标、压力偏差百分比为纵坐标，画出不同线路不平顺下制动盘压力偏差百分比曲线，如图15~16所示。从图中可以看出，无论是常用制动还是紧急制动，随着线路谱幅值放大倍率θ增加，制动压力的最值和压力偏差百分比都随之增大；当线路谱幅值放大倍率θ为2时，常用制动压力偏差百分比为-5.95%~6.56%；紧急制动压力偏差百分比为-4.43%~4.94%。这是因为，随着线路谱幅值放大倍率θ增加，线路条件也越差，线路不平顺波动越大，这也意味着此时制动盘震颤得更厉害，因此压力偏差值也会因为制动盘晃动增大而增大。

　　3结束语

　　本文分析了不同工况下的制动盘力承载边界，通过对高速列车动力学模型进行仿真研究，得到如下结论。

　　（1）制动过程中由于轨道不平顺的激扰，导致制动盘与夹钳产生横向位移，引起同一制动盘左右两侧的制动压力发生波动。此外，随着车辆运行速度的降低，制动盘与夹钳的振动幅度减弱，制动压力、制动摩擦力的波动也逐渐减少。

　　（2）主要研究了线路激扰下制动盘的压力波动特性，初步分析了制动初速度、减速度、轴重以及线路不平顺幅值对制动盘压力波动的影响，计算结果表明：由于受到线路激扰的影响，位于轮对上的制动盘与位于转向架构架上的制动夹钳之间产生相对振动，导致制动压力在额定压力附近波动（约为±5%）。此外，随着制动初速度和线路不平顺的增大、减速度的降低均会加大制动压力的波动。

　　参考文献：

　　[1]付强,卢纯,莫继良.考虑残余应力和制动工况的制动盘热机耦合仿真分析[J].重庆理工大学学报(自然科学),2022,36(4):120-130.

　　[2]GEBREYOHANES M Y,莫继良,楚明,等.制动条件下高速列车轮轨动态响应特性分析[J].重庆理工大学学报(自然科学):2022,36(12):289-296.

　　[3]刘铭倩,姜春鹏,钟升凯,等.城市轨道车辆车内噪声的来源及控制[J].内燃机与配件,2024(01):49-51.DOI:10.19475/j.cnki.issn1674-957x.2024.01.021.

　　[4]杨国伟,魏宇杰,赵桂林,等.高速列车的关键力学问题[J].力学进展,2015,45(1):217-460.

　　[5]张天成.高速列车制动盘热疲劳裂纹萌生机理及磨损性能研究[D].长春:长春工业大学,2023.

　　[6]唐斌,项载毓,范志勇等.沙粒介入高速列车制动界面对摩擦块摩擦磨损行为的影响[J/OL].摩擦学学报:1-15[2024-01-28].https://doi.org/10.16078/j.tribology.2023082.

　　[7]项载毓,莫继良,贺德强等.基于三明治阻尼结构的高速列车制动摩擦振动噪声抑制[J/OL].机械工程学报:1-13[2024-01-28].http://kns.cnki.net/kcms/detail/11.2187.TH.20230922.1441.004.html.

　　[8]WADDAD Y,MAGNIER V,DUFRENOY P,et al.Multiscale thermomechanical modeling of frictional contact problems con‐sidering wear-Application to a pin-on-disc system[C]//22nd In‐ternational Conference on Wear of Materials,Miami,2019,426:1399-1409.

　　[9]丁思源,马蕾,石含波,等.低温环境对高速列车制动盘材料疲劳裂纹扩展性能影响研究[J].机械强度,2022,44(5):1082-1090.

　　[10]孙洪雨,马元明,陈辉,等.高速列车制动材料高温摩擦磨损行为研究[J].机械,2018,45(10):5-10.

　　[11]童欣.基于相变储热原理的高速列车制动盘散热研究[D].北京建筑大学,2023.

　　[12]喻亮,周立智,姜艳丽.SiC3D/Al复合材料高速列车制动盘紧急制动热流耦合有限元模拟[J].热加工工艺,2019,48(12):75-79.

　　[13]周素霞,童欣,孙宇铎,等.基于相变储热原理的高速列车制动盘散热研究[J].机械工程学报,2022,58(6):202-210.

　　[14]张英才.高速列车制动盘散热筋优化设计[J].中国科技信息,2022(10):115-117.

　　[15]吕雪梅,王曦,罗明生.考虑接触热阻的高速列车制动盘热机耦合行为分析[J].机械工程学报,2021,57(22):296-304.

　　[16]钱坤才,吴射章,乔青锋,等.高寒雨雪气候下高速动车组盘片摩擦副摩擦性能[J].西南交通大学学报,2017,52(6):1188-1192.

　　[17]李小彭,岳冰,王丹,等.制动参数对制动系统稳定性的影响[J].振动、测试与诊断,2016,36(1):73-79.

　　[18]BELHOCINE A,BOUCHETARA M.Thermal analysis of a sol‐id brake disc[J].Applied Thermal Engineering,2012,32:59-67.

　　[19]范志勇.摩擦粒子填充对高速列车闸片制动摩擦学行为的影响[D].成都:西南交通大学,2023.

　　[20]陈有洁.摩擦材料对制动温度及摩擦性能的试验研究[D].大连:大连交通大学,2021.

　　[21]吴元科.高速列车闸片摩擦块结构及排布对制动摩擦学行为的影响[D].成都:西南交通大学,2022.

　　[22]项载毓,范志勇,刘启昂,等.高速列车制动闸片摩擦块形状对制动界面摩擦学行为的影响[J].摩擦学学报,2021,41(1):95-104.

　　[23]WANG Z W,CHENG Y,MEI G M,et al.Torsional vibration analysis of the gear transmission system of high-speed trains with wheel defects[J].Journal of Rail and Rapid Transit,2019,234(2):123-133.

　　[24]ZHANG T,CHEN Z G,ZHAI W M,et al.Establishment and val‐idation of a locomotive-track coupled spatial dynamics model considering dynamic effect of gear transmissions[J].Mechanical Systems and Signal Processing,2019,119:328-345.

　　[25]曾梁彬,孟永帅.动车组制动夹钳悬吊刚度对频率响应特性的影响[J].中国铁路2019(2):82-88.