摘要：短期电力负荷预测是电力部门生产调度的重要参考，不同地区影响电力负荷的因素有所不同，因此，为探索电力负荷与气象因子之间的因果关系，以某变电站逐小时电力负荷和气象要素数据为基础，采用格兰杰因果检验分析气象要素与电力负荷的因果关系。采用ADF检验验证气象因子与电力负荷数据的平稳性，将通过ADF检验的平稳性变量进行格兰杰因果检验。结果显示，温度、相对湿度和风速均是电力负荷的格兰杰原因，温度和相对湿度对电力负荷变化的影响是实时的，风速对电力负荷变化的影响具有1 h以上的滞后性。采用灰色关联度和余弦相似度建立综合相似性指标，基于相似日法提出一种短期电力负荷预测模型，以2018—2020年的气象数据和电力负荷数据作为样本库，采用2021年的数据对模型预测准确性进行检验。经验证，模型在天气因子变化不明显或变化缓慢情况下预测准确率为90%以上，可作为电力部门生产调度参考。

　　关键词：短期电力负荷预测，格兰杰因果检验，相似日法

　　0引言

　　随着社会经济高速发展和人民生活质量不断提高，电能作为主要能源渗透社会生活、生产各个方面，电力工业的发展建设对国家各行业起到至关重要的作用[1]。随着智能电网技术的不断发展，电力生产和消费更加市场化，对电能生产与供给规划提出更高要求。电力负荷预测是电力市场交易的重要依据之一，其准确性和实时性对电力系统运行的安全性、稳定性、经济性具有重要意义[2]。

　　国内外众多学者对电力负荷的影响因素和预测方法进行了大量的研究。许多学者的研究表明，气象因素是导致电力负荷产生变化的关键因素。早在20年前就有学者在能源消费结构变化与气候特征分析中证实，电力负荷与气温的线性关系在不断增强[3]。冯瑶等[4]在分析了电力负荷与多种气象因子之间的相关性后指出，气温是使电力负荷产生变化的最敏感要素。安徽、湖北、江苏、河北、上海等多地的学者均发现气温是影响电力负荷变化的重要气象要素，并以气温为主要因子建立了电力负荷预测模型[5-10]。除气象要素外，周末／节假日效应对电力负荷的分布也有一定影响。张彦恒等[11]发现冀北地区日最大电力负荷的周变化呈单谷型分布；汪付华等[12]在对淮北市电力负荷进行预测时对周末／节假日的预测结果进行了订正。

　　电力负荷预测按预测时间可分为长期、中期、短期、超短期和特殊日［13］，其中短期电力负荷对电力系统的生产与调度至关重要。DRYAR H A［14］对电力负荷预测的研究起步较早，美国早在1949年就有学者研究了天气与电力负荷的关系，并根据不同天气类型指导电力负荷调度。

　　SAVI S等［15］通过研究电力负荷与冷暖气团维持的关系，采用支持向量机模型对当地电力负荷进行了预测。我国也有许多类似的研究成果，李湘华等［16］引入综合气象指数，基于差分法建立了多元线性短期电力负荷预测模型，对湖南省夏季日最大负荷进行预测，取得了良好的效果；王惠中等［17］在引入综合气象指数的同时，结合了预测日期类型，采用最小二乘支持向量机的方法建立预测模型，提高了电力负荷预测的准确率。在电力部门的研究中，多将相似日法与机器学习法相结合进行短期电力负荷预测，王瑞等［18］运用相似日选择与长短期记忆的短期负荷双向组合预测方法，提高了短期电力负荷预测的精度；马立新等［19］提出了一种基于特征提取相似日的极限学习机（ELM）方法，提高了短期电力负荷预测的精度与速度；陈弘川等［20］采用果蝇优化算法对相似日模型进行了智能优化，使得短期电力负荷预测准确率明显提高。随着人工智能技术的兴起，以大数据和数据挖掘为基础的深度学习方法在电力负荷预测中得到了广泛应用。董彦军等［21］综合考虑了时间日期因素和气候因素，采用随机森林和长短期记忆网络结合的混合模型，有效地提高了短期电力负荷的精度；孔祥玉等［22］采用深度信念网络（DBN），在训练样本大且负荷影响因素较多的情况下，有效提高了电力负荷预测精度。短期电力负荷预测主要是对电力负荷功率的预测，是电力部门生产调度的重要参考，其准确性和实时性对电力系统运行至关重要。针对短期电力负荷预测的研究多是以日最大电力负荷预测为主，对逐小时电力负荷的精细化预测较少。以逐小时电力负荷和气象要素数据为基础，分析电力负荷与气象要素的因果关系，基于相似日法提出一种短期电力负荷预测模型，对逐小时电力负荷进行预测，并用实际负荷数据对模型进行检验，分析不同类型天气下预测模型适用性，以期对特定区域的电力负荷调度提供参考。

　　1资料和方法
       1.1资料来源

　　所用资料为某110 kV变电站2018年1月1日—2021年10月28日逐小时电力负荷平均功率数据；气象数据为同期的逐小时温度、相对湿度、平均风速以及天气现象，来自某国家气象观测站。

　　1.2研究方法

　　1.2.1 ADF检验

　　为采用格兰杰因果检验分析逐小时温度、相对湿度、风速与电力负荷之间的因果关系，首先对变量进行平稳性检验。采用ADF单位根检验对逐小时气象要素（温度T、相对湿度VRH、风速F）变量和电力负荷变量P进行平稳性检验，对未通过ADF检验的变量进行一阶差分处理［8］，然后再进行格兰杰因果检验。

　　对温度T、相对湿度VRH、风速F、电力负荷P分别采用公式（1）建立自回归模型：

　　Xt=λXt-1+ωt（1）

　　式中：X为时间序列变量（温度T、相对湿度VRH、风速F、电力负荷P）；ωt为白噪声。

　　对回归系数λ进行显著性检验，若λ显著等于1，则表示变量X存在单位根，为不平稳性变量；若λ显著小于1，则表示变量X不存在单位根，为平稳性变量。

　　1.2.2格兰杰因果检验

　　采用格兰杰因果检验对气象要素（温度T、相对湿度VRH、风速F）与电力负荷P之间的因果关系进行分析。格兰杰因果检验是通过定量分析一个变量X的变化是否能够预测另一个变量Y的变化，进而判断变量X是否为导致变量Y的原因［23］。以温度T与电力负荷P两个变量为例，采用式（2）、（3）建立格兰杰因果检验计算模型。

　　式中：α0为常数项；p和q分别为电力负荷变量P和温度变量T的最大滞后期数；μt为白噪声。

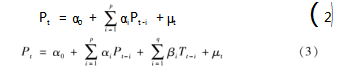
　　式（2）为P对P的滞后项Pt-1，Pt-2，…，Pt-p的回归，但在这一回归中没有把温度变量T的滞后项包括进来，这是一个受约束的回归，从此回归得到受约束的残差平方和RSSr；式（3）在式（2）的基础上加入了温度变量T的滞后项，是一个无约束的回归，由此回归得到无约束的残差平方和RSSu。利用RSSr和RSSu构造统计量F：

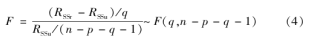
　　式（4）中n为样本容量。检验温度变量T是否为电力负荷变量P的格兰杰原因的具体方法是判断F统计量的临界值是否大于F分布的标准值，若临界值的概率小于0.05，则表示通过检验［24］，即温度变量T是引起电力负荷变量P变化的原因。

　　1.2.3基于相似日法的电力负荷预测模型

　　将2018—2020年（共1096 d）数据作为样本组，样本组中每日的气象数据（逐小时温度、湿度、风速）构成的气象特征向量Xi组成样本库；将2021年（共301 d）数据作为检验组，检验组某日（即预测日）的气象特征向量为X0。

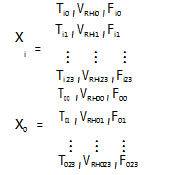
　　式中：Ti0~T i23为样本组中第i日逐小时温度，℃；VRHi0 VRHi23为第i日逐小时相对湿度；Fi0~Fi23为第i日逐小时平均风速，m/s；T00~T023为预测日逐小时温度，℃；VRH00VRH023为预测日逐小时相对湿度；F00~F023为预测日逐小时平均风速，m/s。

　　采用灰色关联度Ri结合余弦相似度Dcosi构建综合相似性指标Si，用来量化样本库中Xi与预测日X0的相关关系。灰色关联度Ri表示样本库中Xi与预测日X0的总i值越接近于1表示越相关。灰色关联度计算公式如下：

　　式中：εi（k）为预测日与样本库中气象特征分量（温度分量、相对湿度分量、风速分量）之间的关联系数；为气象要素的个数（本文m=3）。

　　关联系数计算公式为：

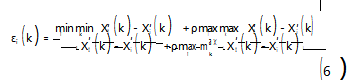
　　式中：X′（k）为第k个气象特征向量归一化后的值；ρ为介于0~1的分辨系数，一般取ρ=0.5。

　　余弦相似度Dcosi反映样本库中Xi与预测日气象特征向量X0的变化趋势的相似性，D cosi值越接近1表示越相关。余弦相似度计算公式为：

　　式中第i个样本库中的第k个气象特征向量分量。

　　综合相似性指标Si计算公式为：

　　式中：α为经验权重系数，结合具体天气情况取值，当气象因素发生剧烈波动时，α取值应接近0，否则接近1。

　　选取样本库中综合相似性指标Si最高的5日作为相似日样本D1~D5，根据式（9）得出预测日逐小时电力负荷值。

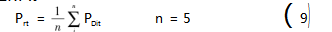
　　式中：Prt为预测日t时刻电力负荷预测值；PDit为相似日样本中Di日t时刻的电力负荷值。

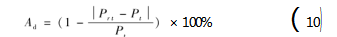
　　1.2.4准确性检验

　　根据2021年逐小时电力负荷实际值对模型预测结果的准确性进行检验。采用式（10）计算预测准确率，其中Prt某时刻电力负荷预测值，Pt为该时刻电力负荷实际值，A d为该时刻电力负荷预测准确率。

　　2结果与分析

　　2.1电力负荷与气象因子因果关系分析

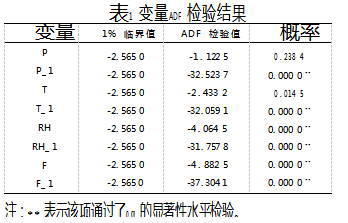
　　为分析电力负荷与气象因子之间的因果关系，首先采用SPSS对温度T、相对湿度VRH、风速F、电力负荷P进行平稳性检验。表1为各变量ADF检验结果。其中P_ 1、T_ 1、RH_ 1、F_ 1分别表示一阶差分后的电力负荷、温度、相对湿度、风速变量。可以看出，逐小时温度T和电力负荷P两个变量原序列未通过ADF检验，不是平稳性变量，不能进行格兰杰因果检验；经一阶差分后的P_ 1和T_ 1均通过了平稳性检验，在进行格兰杰因果检验时，采用一阶级差分后数据进行检验。相对湿度VRH和风速F及一阶差分后的RH _ 1和F_ 1均通过了ADF检验，可直接进行格兰杰因果检验。

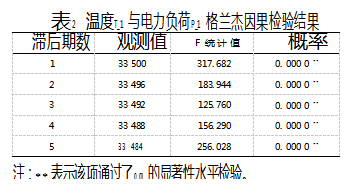
　　采用EViews软件对一阶差分后的温度T_ 1和电力负荷P_ 1进行格兰杰因果检验，从1~5个不同的滞后期数揭示温度对电力负荷影响的时期特征。如表2所示，在不同滞后期情况下均通过了0.01显著性水平的检验，这表明温度是电力负荷的格兰杰原因，即温度的变化能够造成电力负荷的变化，且5 h之内的温度变化均会对某时刻的电力负荷变化产生影响，二者之间存在因果关系。

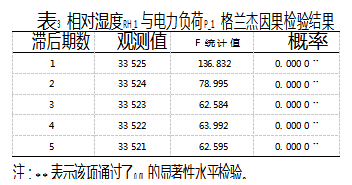
　　同样采用1~5个不同的滞后期数分析相对湿度VRH和风速F对电力负荷影响的时期特征。表3和表4分别为相对湿度和风速与电力负荷的格兰杰因果检验结果。

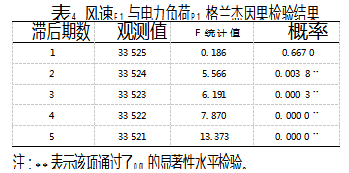
　　可以看出，相对湿度在不同的滞后期情况下均通过了显著性检验，表明相对湿度是电力负荷的格兰杰原因，电力负荷对相对湿度的变化响应较为敏感。风速在滞后期2~5时对电力负荷的影响显著，表明风速对电力负荷的影响有滞后性，滞后期超过1h。

　　2.2电力负荷预测及检验

　　2.2.1算例分析

　　为检验不同天气类型情况下电力负荷预测效果，从检验组中分别选取晴天、雨天、复杂天气（冰雹，雨天）3种天气类型典型日，采用相似日法计算样本与典型日的综合相似性指标Si值，筛选出Si值最大的5日对典型日的逐小时电力负荷值进行预测，并与实际电力负荷进行对比分析。表5为选取的不同天气类型典型日，以及通过计算Si筛选出的相似日。

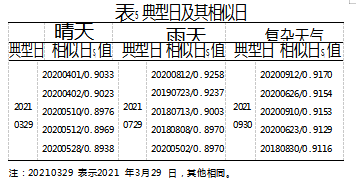
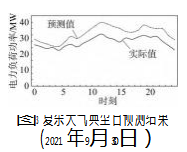
　　根据筛选出的相似日对晴天天气状况下电力负荷进行预测，以2021年3月29日为例，图1为该日逐小时电力负荷预测结果。从图中可看出，预测值与实际值变化趋势整体一致，其中夜间(0时—07时，19时—23时）预测值与实际值差别较小，主要是晴天天气状况下，夜间气象要素变化较平稳，且用电组成较单一，预测准确性较高。

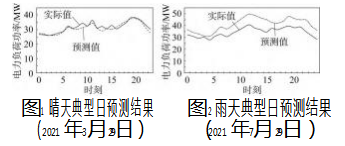
　　图2所示为雨天天气状况下电力负荷预测结果。该典型日天气状况为小雨，连续性降水。从图中可看出，虽然预测值与实际值变化趋势整体一致，但整体比实际值值高，差值在12时—14时最大。经分析，筛选出的5个相似日中仅2020年8月12日有小雨且降水时间较短，其他相似日为轻雾或晴天，无降水天气，在模型计算过程中未考虑降水对电力负荷的影响，导致预测结果整体偏高。该典型日降水自02时开始持续至23时，且在15时—19时为中雨，在优化模型时，也应考虑降水持续时间和降水强度的影响。

　　复杂天气情况下电力负荷预测结果如图3所示。该典型日天气状况较复杂，0时—02时降水为小雨转中雨，03时—07时为晴天，08时开始出现间歇性小雨和中雨，13时出现冰雹，15时之后为晴天，21时开始出现轻雾。由图3可看出，复杂天气下实际电力负荷波动性较大，这表明剧烈的天气变化对电力负荷的影响较大，电力负荷存在较大的随机性和波动性，预测准确性较低。

　　2.2.2模型检验

　　为验证电力负荷预测模型整体的准确性，运用Python编程对检验组逐小时电力负荷进行预测，用实际电力负荷对预测效果进行检验，并对不同天气状况下的平均预测准确率进行统计。

　　根据观测的天气现象对2021年逐小时电力负荷预测准确率进行统计分析，观测的天气现象分类依据为地面气象观测相关技术规定[25]。表6所示为不同天气现象时的平均电力负荷预测准确率。可以看出，在晴天或无明显天气情况下预测准确率在90%以上，霾和轻雾天气情况下准确率在88%以上，降水强度较小时（小雨、毛毛雨）预测准确率在85%以上，在间歇性降水（中雨、大雨）和冰雹情况下预测准确率均较低(76%~82%),这表明在天气较稳定情况下，预测效果较好。根据日平均电力负荷预测准确率统计，有连续降水或剧烈天气变化（冰雹）日期(18 d)的日平均电力负荷预测准确率为77.36%,其他日期平均预测准确率为90.05%,这也表明该模型在无明显天气变化或轻微降水天气情况下预测效果较好。

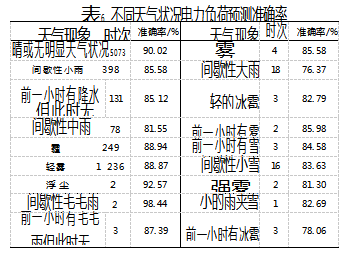
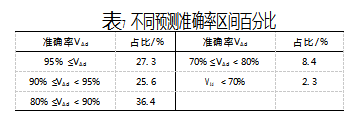
　　表7所示为不同预测准确率区间占比。可看出，准确率超过90%的数据占所有数据的52.9%,超过一半以上，准确率小于80%的数据仅占10.7%,表明该模型整体预测结果较好。

　　3结束语

　　为了提高短期电力负荷预测精度，提升气象保障能源供给能力，保障电力安全稳定运行，分析了气象要素与电力负荷之间的因果关系，基于相似日法提出一种短期电力负荷预测模型，得出以下结论。

　　(1)格兰杰因果检验表明，抚宁某地的气象要素与电力负荷有着明显的因果关系，逐小时温度、相对湿度、风速均是电力负荷变化的格兰杰原因。其中温度和相对湿度在1~5个滞后期都表现出对电力负荷的影响特征，风速在2~5个滞后期对电力负荷影响显著，表明电力负荷对温度和相对湿度的变化响应较快，而风速对电力负荷的影响存在1h以上的滞后期。

　　(2)典型日预测结果表明，在晴天天气状况下模型的预测值与电力负荷实际值变化趋势整体一致，夜间预测效果更好；雨天天气状况预测值整体高于实际值；复杂天气对电力负荷的影响较大，实际电力负荷存在较大的随机性和波动性，预测难度较大。

　　(3)预测模型在天气状况变化不明显或变化缓慢情况下预测准确率为90%以上，预测效果较好，可作为电力部门生产调度参考。在天气变化剧烈情况下预测准确率明显偏低，这主要与模型本身参数设定有关。此外，电力负荷与节假日、季节等因素有关，在后续的研究与应用中，应深化电力负荷与各因素之间关系的分析，细化天气类型，优化模型参数，以期提高预测精度，增强模型的实用价值。

　　参考文献：

　　[1]王栋．电力系统负荷预测综述[J].电气开关，2020,58(1):6-8,20.

　　[2]钱育树，孔钰婷，黄聪．电力负荷预测研究综述[J].四川电力技术，2023,46(4):37-43,58.

　　[3]袁顺全，千怀遂．我国能源消费结构变化与气候特征[J].气象科技，2003(1):29-32.

　　[4]冯瑶，金顺梅，董元元，等．长春市电力负荷与气象要素相关分析[J].气象灾害防御，2017,24(01):15-20.

　　[5]吴迪，王正风．气象敏感性负荷特性分析及预测[J].东北电力技术，2020,41(1):4-8.

　　[6]任永建，熊守权，洪国平，等．气象因子对夏季最大电力负荷的敏感性分析[J].气象，2020,46(9):1245-1253.

　　[7]李艳，俞剑蔚，蔡芗宁，等．南京市电力负荷特征及夏季极端负荷与气象条件关系[J].气象科技，2021,49(4):637-646.

　　[8]张海东，孙照渤，郑艳，等．温度变化对南京城市电力负荷的影响[J].大气科学学报，2009,32(4):536-542.

　　[9]张振，聂建春，萨仁高娃，等．基于内蒙古区域气候特征的110 kV变电站建筑节能分析[J].内蒙古电力技术，2021,39(6):33-39.

　　[10]刘红亚，曹亮．上海市电力负荷与气象因子关系及精细化预报[J].应用气象学报，2013,24(4):455-463.

　　[11]张彦恒，杨琳晗，武辉芹，等．冀北电网电力负荷特征与气温的关系[J].干旱气象，2016,34(5):881-885.