摘要:政策性银行的负债核心依赖政策性金融债发行,且近年面临净息差下降的经营压力,发行利率的精准预测是其“择机发债、控制成本”的关键前提。本文以2019年1月—2024年12月政金债发行数据为训练基础,整合宏观经济、资金供给、债券要素三大维度的17项核心指标,构建了BP神经网络回归、随机森林回归和支持向量机(SVR)回归3种机器学习的预测模型。通过2025年1—6月的实际发行数据验证显示:3种模型对政金债发行利率的预测走势与实际走势高度吻合,其中随机森林回归表现最优,对国开债的预测精度尤为突出(MSE=0.015,R2=0.987);国开债整体预测效果优于农发债和口行债,后两者因数据特征变化(如农发债浮动利率债券占比变动)和积累程度差异存在一定偏差。研究表明,机器学习模型可有效捕捉政金债利率波动规律,为政策性银行择机发行提供科学参考。

　　关键词:政金债;发行利率;BP神经网络回归;随机森林回归;支持向量机(SVR)回归

　　0引言

　　研究聚焦机器学习在政金债发行利率预测中的应用,主要是由于政策性银行(包括国家开发银行、中国农业发展银行和中国进出口银行,以下简称国开行、农发行和进出口行)降低发行债券成本的实践需求。上述政策性银行因无法吸收居民存款,负债核心依赖政金债发行,而近年来银行业整体受净息差持续收窄影响,其经营业绩面临下行压力。发行利率的高低直接决定融资成本,精准的预测工具可助力政策性银行把握“低利率窗口期”。因此,开发精准的预测工具,服务于政策性银行“降本增效”的经营管理目标,显得尤为迫切。

　　党的二十大明确提出“坚持把发展经济的着力点放在实体经济上”[1],而政策性银行作为服务实体经济的“国家队”,其融资成本直接影响基建、三农、科技创新、进出口贸易等国家重点战略领域的资金供给成本。2023年中央金融工作会议首次将“坚持把金融服务实体经济作为根本宗旨”写入中国特色金融发展之路,明确金融需为高质量发展提供“优质服务”[2]。政策性银行承担棚改、农业、水利、基础设施建设等公益性项目,传统的“国债加点”价格预测模型难以应对“低收益+长周期”的资金匹配需求。研究通过机器学习捕捉利率波动规律,突破传统线性思维局限,帮助政策性银行以更低成本筹集资金,确保政策性贷款利率低于市场水平,高效履行政策性金融职责。

　　近几年,面对复杂多变的内外部环境,我国宏观经济运行和银行业发展均展现出较强韧性。政策性银行在保持稳健经营的同时,受净息差下降等多方面因素影响,经营业绩也面临下行压力。发债作为其主要筹资方式,面临“发债成本市场化”与“贷款利率政策性”的机制性矛盾:一方面,负债端高度依赖政金债发行,其利率由市场招标决定,受财政政策、货币政策、市场资金、投资者情绪等多重因素影响呈现周期性波动,市场化特征突出;另一方面,资产端贷款利率受政策调控刚性约束,需保持低于商业贷款利率的水平,重点支持国家政策保障领域,利率水平有一定限制。这种“负债端随市场浮动、资产端由政策锁定”的格局,导致政策性银行息差持续承压。

　　当前金融科技处于快速发展阶段,以DeepSeek、ChatGPT等代表的大语言模型正深刻重塑金融领域的底层逻辑。这些机器学习模型凭借海量数据学习能力,在预测价格等方面展现出较大的潜力。在政策性银行债券发行工作前,引入机器学习模型预测发行利率,是金融科技与政策金融深度融合的创新实践。此前金融科技在债券领域的应用多聚焦国债、地方政府债,且以传统模型为主;而机器学习模型(如随机森林、BP神经网络)具备的海量数据学习、非线性拟合、抗过拟合等优势,尚未有效应用于政金债场景—可以帮助政策性银行整合多维度指标、动态捕捉市场规律的量化工具,以满足政金债发行利率“精细化预测”的需求,符合金融科技与政策金融深度融合的行业趋势。

　　通过机器学习优化政金债发行利率预测,既契合顶层设计的政策导向,又精准破解了政策性银行“市场化发债成本波动与政策性贷款利率息差失衡”的核心痛点,是推动科技、产业与金融深度融合的典型实践。目前机器学习模型在政金债发行利率预测中的系统性研究尚属空白,而本研究构建的“多维度指标整合+多模型对比”框架,可推广应用于国债、地方政府债等其他债券的利率预测研究,具备较强的行业参考价值。

　　1概念、理论和文献

　　1.1主要概念的内涵和外延

　　1.1.1政策性银行

　　政策性银行是由国家设立、承担政策性金融服务职能的特殊金融机构,不以盈利为首要目标,依托国家信用发债筹资,服务实体经济重点领域,无法吸收居民存款,负债主要依赖政金债发行,主要包括国开行、农发行和进出口行,在实现政府发展目标、弥补市场失灵、提高资源配置效率、平抑经济周期性波动等方面起到积极作用。其中,国开行聚焦基建、科技创新、区域协调发展等领域;农发行:聚焦乡村振兴、农业农村基础设施、粮食安全等领域;进出口行聚焦外贸、跨境投资、国际合作等领域。

　　1.1.2政金债

　　政金债即政策性金融债券,是政策性银行为筹集负债资金发行的债券,核心特征是以国家信用为隐性支撑,信用利差极小,发行利率定价需以国债利率为无风险基准,叠加财政政策、货币政策、市场资金、投资者情绪等非信用因子,是我国利率债的重要组成部分。1994年国开行发行首只政金债,当年发行量不足500亿元;品种以3~5年期固定利率债为主,成为商业银行低风险资产配置的重要选择,为后续市场化改革奠定基础。2005年国开行首次采用“公开招标发行”,引入荷兰式招标、美式招标等市场化定价方式,发行利率由市场供需决定,打破“行政指导加点”模式。2014年政金债全年发行量突破3万亿元,较1994年增长60倍;在银行间债券市场存量占比达25%,超越企业债,成为仅次于国债的第二大利率债品种,进入成熟发展阶段。截至2024年末,在我国金融债市场中,政金债占据重要地位,其存量规模是四大国有商业银行债券的2.92倍,其中国开行债券(以下简称“国开债”)存量规模最大,占政金债存量规模的49.02%(见表1)。

　　1.1.3政金债发行利率

　　政金债发行利率核心是一般通过荷兰式招标机制,由参与承销做市的金融机构共同博弈确定参考收益率,最终形成反映市场供需、契合政策性银行负债需求的实际利率。政金债发行利率并非由单一主体决定,而是承销做市机构基于自身经营目标与市场判断的集体决策结果,核心参与主体的角色的差异,共同影响利率形成。政策性银行作为发行人,在发行前公布债券发行规模、期限、招标时间等要素,承销资格的机构(如商业银行、证券公司、保险公司等)根据自身资金成本、市场利率预期、资产配置需求,独立报出“希望认购的收益率水平”;发行人按“报价从低到高”排序,累计中标量达到发行规模时,最后一个中标报价即为“中标收益率”,所有中标机构均按该收益率认购债券,该中标利率即为该次招标的发行利率。

　　1.2理论基础

　　研究围绕“政金债发行利率预测”构建机器学习模型,其理论支撑源于多学科交叉领域,既包含金融领域的债券定价理论、政策性金融特性理论,也涵盖机器学习领域的模型算法理论,同时融合宏观经济与资金市场的联动理论,共同构成研究的核心理论框架。

　　1.2.1债券定价与利率决定理论

　　政金债作为利率债的核心品类,其发行利率定价需遵循债券市场基本规律,同时兼顾政策性金融的特殊属性,其债券定价主要基于无风险利率基准与利差定价理论。核心内涵该理论认为,政金债因依托国家信用隐性支撑,信用风险极低,其定价需以“无风险利率”(国债收益率)为基准,通过叠加“非信用利差”(政策、流动性溢价、税收差异、市场情绪等)形成最终发行利率。研究中文献综述明确这一逻辑,马光荣等[3]提出的“信用混同”理论指出,政金债与地方政府债类似,受国家信用助推,信用利差极小,因此定价需首先锁定国债利率基准。

　　1.2.2多因子利率决定理论

　　传统单因子定价模型(如仅依赖国债利率)无法充分解释政金债利率波动,多因子理论认为,利率是宏观经济、资金供给、债券自身要素等多维度因素共同作用的结果。具体而言:宏观经济因子(如CPI、PPI)通过影响通胀预期决定利率中枢;资金供给因子(如DR007、存款准备金率)反映市场资金松紧,直接影响短期利率波动;债券要素因子(如发行期限、发行量)则通过供需关系形成微观定价差异。

　　2文献综述

　　预测及测算政金债发行利率是一项综合性任务,包含宏观经济、制度背景、市场微观结构与计量模型等多个思路,现有研究为建立定价模型提供丰富理论基础和方法参照。

　　定价的重点逻辑需顾及中国债券市场的特殊制度背景,马光荣等[3]研究地方政府债时提出“信用混同”问题,即省级政府隐性背书使债券发行利率与真实信用风险脱节,政金债跟地方债主体虽不同,但国家信用的强力助推让其信用利差极小。所以,任何定价模型都要把这一种制度性信用帮扶当作基本前提,价格预测需首先锁定无风险利率基准,比如国债利率,基础利差模型可以概括为政金债发行利率与同期限国债利率的差值。该利差重点体现了流动性、税收差异等非信用因子,而非违约风险。

　　精确的定价模型需要逐步加入市场化因子。张欣怡提到,理想的政府类债券价格形成机制,应参照国债价格,同样体现资金市场供需以及项目收益等信息,这为政金债定价给出了方向:预测模型需由单一基准转向多因子共同作用。模型可设计为一种融合函数[4]。这要求模型重视招标倍数、货币市场利率、宏观经济景气度等变量。公式为

　　预测价格=f(基准利率,市场流动性,宏观经济指标,债券供需关系)

　　宏观思路来看,具体经济变量的选择非常重要,Rahmatika和Fachmi借助向量误差修正模型(VECM)探究了宏观经济因子和政府债券收益率之间的关系,发现基准利率、货币供应量、外汇储备以及外部市场波动等都属于明显因子[5]。这说明政金债定价预测可以需要抓住价格与各宏观变量间的长期平衡关系及短期动态变化。

　　在定价模型方面,Kawakatsu提出,定价模型需要依靠基准收益率曲线的准确测算,使用动态Nelson-Siegel-Svensson(NSS)模型可以预测拟合收益率曲线,这一模型能妥善解决期限两端数据不足的问题,同样反映收益率曲线的变化趋势。在政金债定价前,可借助NSS模型生成更准确的基准收益率曲线[6]。

　　但基准曲线建立本身带有不确定性,Díaz等的研究指出,即便使用相同的拟合技术,选择用来建立收益率曲线的样本券(如是否包含新发债、高流动性券等)也会让曲线形态发生明显变化,这对政金债定价的启发是,利用国债或政金债自身历史数据建立基准曲线时,要谨慎挑选样本券,同样实行稳定性检验,减少模型风险[7]。

　　研究文献综述明确,政金债发行价格预测是一项融合政策逻辑与市场规律的综合复杂工程,当前政金债发行利率预测领域,机器学习模型在政金债发行利率预测中的系统性研究尚属空白,而本研究构建的“多维度指标整合+多模型对比”框架,可推广应用于国债、地方政府债等其他债券的利率预测研究,具备较强的行业参考价值。

　　3研究逻辑与路径

　　研究围绕政金债发行利率精准预测核心目标,遵循“问题提出—理论支撑—数据准备—模型构建—实证验证—结论优化”的科学研究逻辑,结合政策性银行债券发行规律与金融科技发展趋势,形成完整研究框架,具体研究路径见图1。

　　4研究设计

　　4.1数据处理

　　1.指标选取

　　在债券发行利率的定价逻辑中,宏观经济、资金供给和债券要素等3个维度的17个核心指标共同构成了影响因素体系,每个指标通过不同机制影响发行利率。具体分类及影响逻辑见表2。

　　在债券发行利率的预测模型中,需要排除一部分具有滞后性的指标,债券发行利率的预测是对市场当前定价共识的捕捉,虽然有部分指标对债券发行利率也有一定的影响,但这些指标因为滞后性、信息延迟、关联性弱化等问题,难以满足模型对即时性、准确性的需求,因此未被纳入预测模型。

　　2.数据预处理

　　政金债的发行规模、期限、关键条款等核心要素需提前向监管部门报备审批,以上变量所采用的数据,均为报备当天的最新数据。本文通过万得金融终端(Wind)和森浦资讯(Quebee),获取2019年1月—2024年12月国开债、农发行债券(以下简称“农发债”)、进出口行债券(以下简称“口行债”)的债券发行利率和变量数据作为训练集,收集2025年1月—2025年6月的债券发行利率和变量数据作为验证数据集。

　　由于影响债券发行利率的17个指标在数值量级、单位、波动范围上差异较大,直接输入模型,会导致量级大的指标(如发行规模)主导模型权重,而量级小的指标(如PMI)被忽略,最终影响预测准确性。本文采用Z-Score标准化的方法对债券发行利率和变量数据统一数值尺度,并运用数据可视化技术绘制了主要变量间的相关系数热力图,直观展示主要变量之间的线性相关性。

　　4.2模型建立

　　1.BP神经网络回归预测模型

　　BP神经网络回归,即误差反向传播神经网络回归,是具有3层或3层以上的多层神经网络模型,每一层都由若干个神经元组成。该模型的左、右各层之间各个神经元实现全连接,即左层的每个神经元与右层的每个神经元都有连接,而上下各神经元之间无直接连接[8],见图2。

　　该模型按照有监督学习方式进行训练,当一对学习模式提供给网络后,其神经元的激活值将从输入层(Input)经各隐含层(Hidden)向输出层(Output)传播,在输出层的各神经元输出对应于输入模式的网络响应,再按照减少希望输出与实际输出误差的原则,从输出层经各隐含层、最后回到输入层逐层修正各连接权。随着以上误差逆传播训练的不断进行,网络对输入模式响应的正确率也将不断提高。

　　本文采用3层BP神经网络回归模型;其中输入层,根据上文筛选出的17个指标,对应设置17个输入层节点;由于本文将预测债券发行利率,因此输出层节点数为1;训练函数调整全局权值和阈值,以实现整体误差最小,本文采用identity激活函数作为模型的训练函数。

　　2.随机森林回归预测模型

　　随机森林回归是一种集成学习算法,通过构建多个决策树,从原始数据集中通过有放回抽样生成多个子数据集,每棵决策树基于不同的子数据集进行训练,降低模型的方差。该模型算法流程见图3。

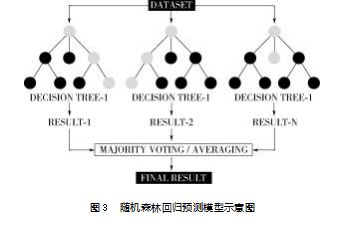
　　在构建回归模型时,通过创建多个决策树进行预测,每个决策树根据输入特征独立生成一个连续的数值预测结果,然后通过对所有决策树预测值取平均值或加权平均值的方式,综合得出最终预测结果。相比BP神经网络的“黑箱”特性,随机森林具有可解释性强、抗过拟合、对异常值稳健等优势,更适配金融场景对模型透明度和稳定性的要求[9]。

　　3.支持向量机(SVR)回归预测模型

　　支持向量机(SVR)回归预测模型源于支持向量机(SVM)的回归拓展,核心思想是通过映射高维空间和容忍误差区间,找到最优拟合超平面。与传统回归模型追求最小化整体误差不同,SVR更关注“让多数样本落在预设误差范围内”,同时最大化超平面与边界样本(支持向量)的间隔,实现泛化能力提升。在支持向量机(SVR)回归中,核函数是其中重要的数学函数,其核心作用是将低维输入空间中的非线性数据映射到高维特征空间,使得原本在低维空间中无法用线性模型拟合的非线性关系,在高维空间中可以用线性模型来近似。

　　本文支持向量机(SVR)回归模型的核函数采用线性核函数,具体数学公式表达如下:

　　K(xi,xj)=xi·xj+c

　　式中,xi和xj是两个样本量的特征向量;xi·xj为xi、xj的向量点积;c为可选常数(本文模型构建中c=0)。

　　5实验结果分析

　　5.1预测效果

　　通过MSE(均方误差)、MAE(平均绝对误差)和R2(决定系数)3个量化指标来衡量训练集的预测效果(见表3)。

　　从表3可以看出,MSE(均方误差)是预测值与实际值之差平方的期望值,取值越小,模型准确度越高;MAE(平均绝对误差)反映预测值误差情况,取值越小,模型准确度越高;R2(决定系数)反映预测值跟实际值的比较,数值越靠近1模型准确度越高。

　　5.2模型表现对比分析

　　1.随机森林回归

　　在国开债、农发债和口行债3类任务中,随机森林的MSE、MAE均最小,R2均最高,该模型的准确度在三者中最高,误差最小,预测值与实际值最为接近。

　　国开债实验结果:MSE计算结果为0.015,比BP神经网络回归低51.6%,比支持向量机(SVR)回归低71.2%;MAE计算结果为0.086,比BP神经网络回归低19.6%,比支持向量机(SVR)回归低47.9%;R2计算结果为0.987,接近完美拟合(R2=1)。

　　农发债实验结果:MSE计算结果为0.014,比BP神经网络回归低44%,比支持向量机(SVR)回归低77%;MAE计算结果为0.083,比BP神经网络回归低21.7%,比支持向量机(SVR)回归低56.7%;R2计算结果为0.985,接近完美拟合(R2=1)。

　　口行债实验结果:MSE计算结果为0.013,比BP神经网络回归低55.2%,比支持向量机(SVR)回归低81.7%;MAE计算结果为0.080,比BP神经网络回归低24.3%,比支持向量机(SVR)回归低61.8%;R2计算结果为0.987,接近完美拟合(R2=1)。

　　2.BP神经网络回归

　　BP神经网络回归表现居中,误差指标(MSE、MAE)和R2均优于支持向量机(SVR)回归,但弱于随机森林回归。原因是BP神经网络虽能拟合非线性,但受限于网络结构、训练参数等因素,若未充分优化,容易出现欠拟合或过拟合;相比集成模型,单网络的泛化能力较弱。

　　3.支持向量机(SVR)回归

　　表现相对较差,在3类债券任务中,MSE、MAE均最大,R2均最低。可能的原因是SVM的性能高度依赖核函数选择和参数调优,若数据存在复杂非线性关系,但使用了线性核(或核函数参数未适配),会导致模型欠拟合。

　　5.3模型预测结果

　　本文以2025年1月1日—6月30日的债券发行利率和变量数据作为验证集,根据3种模型回归预测。预测结果的折线,整体上与实际发行利率折线的走势方向有较高的贴合性。政金债三类模型预测结果与实际发行利率对比见图4。

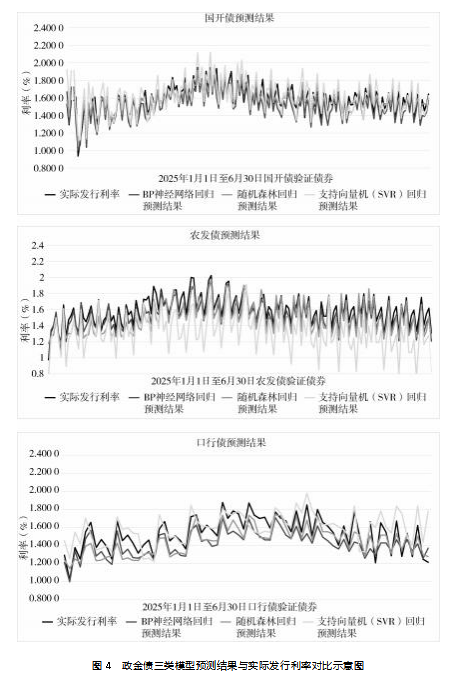
　　从图4可以看出,利率上升或下降阶段,预测折线大多能跟随实际利率的趋势变动,说明模型在捕捉政金债利率整体波动规律上有一定效果。

　　分债券类型来看,国开债采用3种模型回归预测折线与实际发行利率走势贴合度高,上升、下降阶段大多能同步跟随,模型捕捉波动规律效果好,拟合表现最优;农发债和口行债预测折线虽大部分趋势和实际一致,但预测结果与实际偏离更大,说明模型对这两类债券利率波动的精准拟合能力稍弱,原因是农发债、口行债受自身发行特点、市场供需等因素影响,利率波动规律更复杂,增加了模型预测难度。

　　3类债券在3种回归模型下预测差值有一定差异(见表4)。国开债因数据规律稳定与随机森林适配性高而最优;农发债剔除浮息债后,BP神经网络更贴合固定利率债的规律;口行债则因数据不足导致模型表现矛盾。

　　1.国开债

　　随机森林回归预测结果具有绝对优势,准确性与稳定性双优。①准确性最优:预测差值平均值为-0.31BP,是所有债券模型组合中最接近“最优平均值0”的结果,意味着其预测值与实际发行利率的整体偏差极小;②稳定性最强:预测差值标准差仅为6.65,在3类债券的所有模型中最小,说明该模型在不同样本区间的预测波动极低,不会因市场短期变化或数据波动出现大幅偏差;③模型适配性原因:随机森林回归擅长处理非线性数据,而国开债发行规模大、历史数据完整、利率定价逻辑(如对政策利率联动、市场流动性敏感度等)相对稳定,模型能充分学习其规律,因此表现远超其他模型。

　　2.农发债

　　剔除浮息债后模型分层明显,BP神经网络回归模型为最优解。①准确性最优:预测差值平均值为-6.93BP,是农发债预测模型组合中最接近“最优平均值0”的结果;②稳定性最强:固定利率债券的历史数据(2019—2024年)充足,样本分布均匀,BP神经网络模型在训练时能充分学习到农发债稳定的规律,避免了浮息债带来的“变量干扰”,因此标准差(4.64)甚至低于国开债的随机森林模型,稳定性表现突出;③支持向量机(SVR)回归模型随着时间推移,其基于固定核函数和超平面的预测逻辑难以动态调整,进而导致预测差值随时间拉长而显著扩大。

　　3.口行债

　　模型预测结果复杂,核心源于模型特性差异。

　　①准确性维度:支持向量(SVR)回归最优,预测差值平均值为5.94BP,在口行债的3种预测模型中最接近0,说明其对“当前或短期发行利率”的拟合效果更好;②稳定行维度(标准差最小):BP神经网络回归最优,预测差值标准差为8.91,是口行债3种模型中最小的,说明其预测结果的波动更小,但整体偏差(均值)略大于SVR;③随机森林回归模型的优势在于“全局规律学习”,虽然当前均值(分别为-8.85BP大于5.94BP)略逊于支持向量(SVR)回归,但随机森林回归模型的趋势预测更为接近实际发行趋势,且标准差更小,长期预测的稳定性更强。

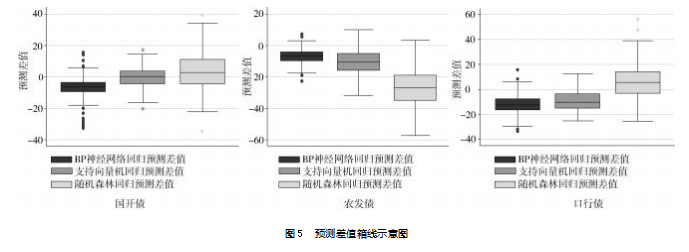
　　3种回归模型预测误差的箱线图见图5,反映出不同模型预测值与实际值的偏差情况。随机森林回归的箱子窄、中位数接近0、须线短,反映出该模型误差小且集中;BP神经网络回归模型箱子宽、中位数稍偏离0,须线相对长,有部分离群点,反映出误差离散程度大,虽多数情况误差不大,但偶尔会出现较大误差;支持向量机(SVR)回归模型箱子最宽、中位数偏离0,须线最长,离群点多,反映出该模型的误差最大、波动最剧烈,预测最不稳定,极端偏差频繁出现。

　　6研究结论和启示

　　6.1本文结论

　　本文基于2019年1月—2024年12月的政金债发行数据,整合宏观经济、资金供给、债券要素三大维度的17项核心指标,构建了BP神经网络回归、随机森林回归及支持向量机(SVR)回归3种机器学习模型,对政金债发行利率进行预测研究,并以2025年上半年实际数据验证模型效果,得出以下结论:

　　1.机器学习模型在政金债利率预测中具备实用价值

　　3种模型均能在一定程度上捕捉政金债发行利率的整体波动趋势,预测走势与实际走势高度吻合。其中,随机森林回归表现最优,在国开债、农发债、口行债3类债券的预测中,均呈现最小的MSE(0.013~0.015)和MAE(0.080~0.086),以及最高的R2(0.985~0.987),误差小且稳定性强;BP神经网络回归表现居中,支持向量机(SVR)回归因核函数适配性等问题,预测误差相对较大。

　　2.不同类型政金债的预测效果存在结构性差异

　　国开债的预测表现整体最优,其中随机森林回归模型对其利率波动的拟合度最高,该模型预测的172个发行利率中,有23条预测数据与实际发行利率相差不足1BP,126条预测数据与实际发行利率相差介于1~10BP,23条预测数据与实际发行利率相差超过10BP;农发债BP神经网络模型预测最优,该模型预测的154个发行利率中,有10条预测数据与实际发行利率相差不足1BP,108条预测数据与实际发行利率相差介于1~10BP,36条预测数据与实际发行利率相差超过10BP,在使用预测结果时,建议结合随机森林回归模型判断;口行债的3种回归模型虽未呈现“单一最优解”,但随机森林回归模型的预测趋势较为接近实际情况,可以作为预测参考。

　　3.模型优化需聚焦数据特征与场景适配性

　　政金债利率预测需兼顾政策逻辑(如国家信用支撑)与市场规律(如资金供需、宏观经济波动),未来可针对农发债、口行债的发行特点,补充差异化特征变量(如浮动利率债券的特定条款影响),并优化模型参数(如SVR的核函数选择);同时,纳入政策突发变动、市场情绪等非结构化因素,可进一步提升模型的泛化能力。

　　综上,机器学习模型为政策性银行择机发债提供了科学参考,尤其随机森林回归在精度与稳定性上的优势使其具备较强的实践应用潜力。后续通过数据迭代与模型迭代的双向优化,可更好地服务于政金债发行决策的精细化需求。

　　6.2研究启示

　　本文以2019年1月—2024年12月政金债发行数据为训练基础,通过多维度指标整合与多模型实证,形成数据处理、模型设计、实践应用3方面的研究启示,为后续政金债利率预测研究与政策性银行决策提供参考依据。

　　(1)数据层面:增加训练数据。由于2018年部分债券发行利率缺失,故本文选取2019年1月—2024年12月政金债发行数据为训练数据,训练数据中有部分时间段处于经济特殊时期,可能存在噪声,未来将政金债发行数据时间跨度进一步拉长,或可进一步提高模型预测的准确性[10]。

　　(2)模型层面:模型选择需匹配债券类型与预测场景,拒绝“单一最优”思维。研究实证显示,随机森林回归因“抗过拟合、可解释性强”,在国开债(数据完整、规律稳定)预测中表现最优,BP神经网络擅长拟合稳定规律,在农发债剔除浮息债后精度显著提升,SVR虽整体表现较弱,但在口行债短期利率拟合中展现“均值最优”优势。这打破“单一模型适配所有场景”的误区,后续研究需建立“债券类型—模型特性”匹配矩阵对发行规模大、数据规律清晰的债券(如国开债),优先选择随机森林等集成模型;对数据波动小、线性关联强的场景(如农发债固息债),可采用BP神经网络;对短期预测需求(如口行债单次发行),可尝试优化SVR核函数以提升非线性拟合能力[11]。

　　(3)应用层面:为政策性银行“择机发债”提供量化工具,缓解息差压力。研究验证的模型可精准捕捉“低利率窗口期”,例如随机森林对国开债的预测差值均值仅-0.31BP,能在政策性银行发行债券前提供决策依据,锁定低成本资金。结合政策性银行“市场化发债成本+政策性贷款利率”的息差矛盾,这一工具可直接转化为经营效益。

　　7结语

　　政金债发行利率精准预测对优化政策性银行发债策略、维护债券市场价格秩序具有重要意义。本研究依托机器学习理论与金融工程学方法,整合宏观经济、资金供给与债券要素多维指标,构建并验证BP神经网络、随机森林回归及支持向量机(SVR)回归3类预测模型,证实随机森林回归在精度与稳定性上表现最优,且国开债预测效果优于农发债、口行债。

　　该研究为政策性银行“择机发债、控本增效”提供量化工具,助力其更好服务基建、“三农”等国家战略领域,契合金融服务实体经济的政策导向。未来研究可重点关注数字化转型背景下大数据、人工智能技术对利率预测模型的优化机制,探索跨市场因子的纳入路径,并针对小样本场景的模型泛化能力提升开展研究,以适应债券市场动态变化。学界与实务界可通过持续深化模型创新与应用实践,不断完善政金债利率预测体系,为政策性银行精细化管理、投资者理性决策及债券市场高效运行提供有力支撑。

　参考文献

　　[1]习*平.高举中国特色社会主义伟大旗帜为全面建设社会主义现代化国家而团结奋斗:在中国共产党第二十次全国代表大会上的报告[M].北京:人民出版社,2022.

　　[2]中国人大网.中央金融工作会议在北京举行:习*平李强作重要讲话,赵乐际王沪宁蔡奇丁薛祥李希出席[EB/OL].(2023-11-01)[2023-10-31].

　　[3]马光荣,宋浩兰,聂卓.信用混同与地方政府债券定价扭曲:兼议完善地方债务管理体制的路径[J].中国工业经济,2025(2):5-22.

　　[4]张欣怡.我国地方政府债券发行市场化水平分析及对策研究[J].学习与探索,2022(6):114-120.

　　[5]RAHMATIKA N,FACHMI M N.Macro economics:liquidity,solvency,and external factor as determinant of government bond index yield(INDOBEXGB)with the vector error correction model(VECM)[J].Riset:JurnalAplikasi Ekonomi Akuntansi dan Bisnis,2020,2(2):326-340.

　　[6]KAWAKATSU H.Recovering yield curves from dynamic term structure models with time-varying factors[J].Stats,2020,3(3):284-329.

　　[7]DÍAZ A,JAREÑO F,NAVARRO E.Yield curves from different bond data sets[J].Review of Derivatives Research,2020,23(2):191-226.

　　[8]周志华.机器学习[M].北京:清华大学出版社,2016.

　　[9]张继德,刘洁,张家轩,等.新质生产力的演进、本质及会计方向研究[J].财会通讯,2025(17):9-16.

　　[10]张继德,张家轩,刘洁,等.2024.企业数字化转型的现实困境、成因和应对研究[J].会计研究(7),13-25.

　　[11]张继德,刘洁,黄思良,等.2023.数字化转型与企业绩效:综述和展望[J].财会通讯(14),3-9,44.