【摘要】针对考虑交付时间窗和机器准备时间的混合流水车间调度问题，以最小化完工时间和最小化提前与拖期加权总和为优化目标，建立混合整数线性规划模型，并根据问题设计一种无参数迭代贪婪算法(ＩＩＧ)。在ＩＩＧ算法中，首先通过三种常用于最小化提前和延迟目标的启发式方法生成解，保留这三者中最优的解作为初始解；其次，采用不需要销毁参数的自适应销毁策略，按照贪婪规则跳过位置，＋－避免非改进插入位置的重构方法；然后，使用邻域插入的局ＴＬＢＯ以及ＰＳＯ四种算法进行２７０个实例实验分析比较，验证了ＩＩＧ算法的有效性。

　　【关键词】混合流水车间调度；序列相关准备时间:交付时间窗；ＩＧ算法

　　混合流水车间调度问题(ＨｙｂｒｉｄＦｌｏｗ－ｓｈｏｐＳｃｈｅｄｕｌｉｎｇＰｒｏｂｌｅｍ，ＨＦＳＰ)是一种复杂的生产调度问题，结合了经典流水车间和并行机调度的特点，是ＮＰ－Ｈａｒｄ问题，广泛出现在汽车、芯片生产、机械制造等规模大、设备多、工序复杂的行业中[１]。在实际生产车间中，在同一台机器上完成一项作业和开始下一项作业之前需要准备时间。作业加工前的准备时间，可以用于对生产机器进行清理、清洗、调整和固定器具等其他生产性操作。大多数的生产线需要生产不同的产品(颜色、尺寸等区别)，所以会频繁在机器上调整准备时间。现有的ＨＦＳＰ文献中，大多以最小化最大完工时间作为目标，但是忽略客户满意度和库存管理，这些可能增加增本、影响企业发展的因素。考虑到时间窗问题的现有文献较少，Ｃｈｅｎ，Ｌｅｅ[２]研究带有到期日窗口的并行机器，证明该问题是ＮＰ－Ｈａｒｄ问题，并提出了求解该问题的分支定界算法。Ｐａｎ等[３]研究具有到期日窗口和以ＴＷＥＴ为目标的混合流水车间问题，提出了改进ＩＧ算法和迭代局部搜索(ＩＬＳ)方法，与其他几种对比算法相比具有竞争优势。田云娜等[４]针对基于时间窗的多阶段混合流水车间调度问题，设计了一种基于时间窗的蚁群算法,以最小化最大完工时间为优化目标,并且与CPLEX相比,设计算法在最大完工时间和计算效率方面均有较大优势。关于机器准备时间方面,Lin,Liao[5]解决了一个基于SDST的两阶段的混合流水车间问题,以最小化加权最大延迟为目标,并提出一种基于特定系统需求的启发式算法。黄辉等[6]研究考虑序列设置时间和工序跳跃的混合流水车间,并提出了一种改进NSGA-II算法,通过对基于实际企业生产数据假设的算例进行仿真求解,表明该算法生成的调度方案能够为企业的实际调度提供有效的方案。陈水琳,郑建国[7]针对考虑序列相关准备时间的分布式混合零空闲置换流水车间调度问题,以最小化最大完工时间、总能耗以及总拖期为目标,构建了DMNIPFSP/SDST问题的数学模型,提出一种多目标灰狼优化算法(Multi-objective Grey Wolf Optimizer,MOGWO)。

　　车间问题(HFSDDW-SDST),设计了一种无参数迭代贪婪算法(IIG),在不同算例情况下与NSGA-II、JAYA、TLBO以及PSO四种算法进行对比实验,证明了该算法的有效性。

　　1问题描述与模型构建

　　1.1问题描述

　　考虑交付时间窗和机器准备时间的混合流水车间调度问题可以描述为:n为在g个阶段中要处理的作业的数量,其中在阶段i(i=1…g)有m台同质并行机。由于本文问题考虑到机器准备时间sijk,所以本文采用最早完成时间规则。每个作业j都有一个交付窗口[dj-,dj+],其中,生产调度期望能够将作业在这个时间窗口交付给客户。如果作业j的完工时间Cj早于时间窗口,则产生一个提前完工时间EJ=dj--Cj;如果作业j的完工时间Cj迟于时间窗口,则产生一个拖期时间TJ=Cj-dj+。不论是提前还是拖后都会产生额外的成本,会对企业产生不利的影响,加入作业提前完工,则会产生额外的库存成本,这些成本同提前时长Ej正相关;假如拖后完工,则会影响客户满意度,为企业带来负面影响,与Tj正相关。调度决策是希望将这n个作业安排到车间进行加工,以获得最小的加权总提前和拖期成本,该问题可以表示为HFSDDW-SDST|

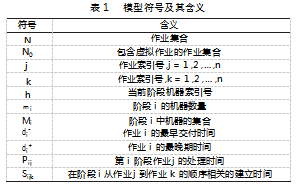
　　1.2模型符号及其含义

　　模型符号及其含义如表1所示。

　　1.3决策变量

　　决策变量符号及其含义如表2所示。

　　1.4目标函数
      

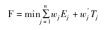
　　以最小化提前和拖期加权总和为优化目标。
      2 IIG算法设计

　　本文设计了一种IIG算法来解决HFSDDW-SDST问题。

　　IIG算法,在初始解生成阶段采用三种启发式方法来对比获得最优初始解,在销毁与重构阶段使用不销毁参数的自适应销毁,以及跳过位置以避免非改进插入的重构方式,来缩短运算时间。算法的主要改进部分包括编码和解码、破坏与重建和局部搜索。以下小节提供了这些操作的具体说明。

　　2.1解的表示和初始化

　　良好的初始解可以显著加快算法的收敛速度。将作业按照简单排序来安排在每个阶段,并按照ECT机器分配规则将作业分配给机器。根据HFSDDW-SDST的特点,本文选择三种常用于最小化提前和延迟目标的启发式方法来获得最优初始解。第一种启发式是最早到期日(EDD)调度方法,按照最晚交付进行排序生成作业的序列π={π1,π2,…,πn}可以表示为d(j)<d(j+1),j=1,…,n-1,其中π(j)为排序π中第j个位置的作业。第二种初始化启发式方法基于Pan等[8]研究的整体松弛时间(OSL),根据每个作业j在所有阶段的总加工时间与其最晚交付时间dj+的差值进行排序,可以表示为d(j)1 p i,π1 p i,π第三种启发式方法根据最后一台机器上的最小松弛时间(LSL)和作业在最后一个阶段的加工时间计算松弛时间(OSL)来进行排序,即d(j)-pg,π(j)≤d(j)-pg,π(j+1),j=1,…,n-1。这三种启发式方法计算非常快,因为只需要计算前述的索引并进行快速排序,复杂度为O(nlog(n))。我们计算EDD、OSL和LSL的序列,保留最优解作为IG的初始解。

　　2.2破坏与重构

　　在贪婪迭代算法(IG)中,破坏与重构是两个关键步骤。在进行破坏阶段时,需要从当前序列Seq1中随机提取d个作业,并放置到置换作业Seq2中。为了保证种群多样性,避免陷入局部最优,本文将破坏参数设置为列表d,最初包括1、2、3和4。每次迭代开始时,从该列表中随机选择一个数值作为当前迭代d的值。每次迭代结束时,如果现有解被接受,则此时d的值将被追加到列表末尾。随着迭代次数增加,列表中将包含更多的最优d值,这可视为一种自我校准。

　　当d个作业被移除,则进入重构阶段。将移除的作业逐个重新插入到部分序列Seq1′中的所有位置,形成新的部分序列Seq1″。在每一次插入时,都对新的部分序列Seq1″进行计算,以此判断此位置是否为改进位置。如果作业插入位置未能改进,将跳过下一个插入位置,重构过程会在找到一个改进的插入位置后,恢复为常规插入。重构阶段的详细操作步骤如下:

　　①根据破坏步骤得到Seq1′、Seq2。

　　②输入Seq1′,Seq2和d。

　　③设置参数为i(i=1,…,d)、Q为Seq1′的规模大小、pos(pos=1,…,Q+1)、增量因子K=1、插入作业Job=Seq2[i]、初始BestFit=999999。

　　④当pos≤Q时,将Job插入Seq1′的pos位置,得到CurrentFit(Seq1′)。

　　⑤如果CurrentFit(Seq1′)<BestFit,则更新BestFit、BestSeq,新的BestFit=CurrentFit(Seq1′)。K依然为1,Job的下一个插入位置为new_pos=pos+K。

　　⑥如果CurrentFit(Seq1′)≥BestFit,则BestFit、BestSeq保持不变,new_K=K+1,Job的下一个插入位置为new_pos=pos+new_K。

　　⑦输出BestFit、BestSeq。
       2.3局部搜索

　　局部搜索过程仅使用插入邻域,操作过程如下:首先,将当前解π2中的第一个作业移到新的随机位置。如果新序列π的目标值Fit(π)小于当前序列的目标值Fit(π2),则用π替换π2。一旦找到改进解,该作业将不再参与后续的插入操作,局部搜索将从第一个作业重新开始。如果没有找到改进解,则继续移动下一个作业,直到所有作业都检查完毕[9]。
       2.4接受准则

　　当一次贪婪迭代算法(IG)迭代结束时,得到新的解π3,并需要决定π3是否成为新的当前解。我们将π3的目标值Fit(π3)与当前解的目标值进行比较。并创建一个列表R用于存储最近访问解,列表R初始为空,每次当算法找到一个新的历史最优解(经过局部搜索后),该列表会被清空,并将此新最优解加入列表中。如果局部搜索得到的解π3并不是历史最优解,那么它将被添加到列表R的末尾。这样,列表R就包含了自从上一次找到最优解以来的所有解。接下来,更新比赛规模的值,如果Fit(π3)小于R中所有解的平均目标(AvgFit),则TS增加1;否则,TS减1(TS的最小值为2,最大值为7)。

　　最后,为了判断是否用新解π3替换当前解,本文应用一种类似遗传算法中的“比赛选择”操作。从R中随机选择TS个元素进行一次“比赛”,即从所选的TS个解中选择目标值最优的解来替换当前解。

　　通过这种方式,增加TS的值可以加强对当前解的局部搜索,使当前解不太可能被替换;而减少TS的值则可以增加解的多样性,使当前解更有可能被替换。由于TS的值是动态变化的,我们在接收新解的准则中加入了一个自适应机制。这样的设计旨在平衡算法在探索当前解附近区域的深度和在解空间中保持多样性的能力。

　　3仿真测试与分析

　　为了验证IIG算法对解决HFSDDW-SDS问题的有效性,将IIG与NSGAII、JAYA、TLBO、PSO四种算法进行比较。五种算法都使用Java语言并采用Eclipse IDE 2022.09进行编程,在Windows11,AMD Ryzen 7 4800H with Radeon Graphics 2.90 GHz,内存16GB,64位操作系统,基于x64的处理器的计算机上运行。

　　3.1算法参数

　　NSGA-II的交叉概率为0.9,变异概率为0.1。所有算法的通用设置为:最大迭代次数G=600、种群规模S=50。

　　3.2测试实例参数

　　为了能够科学有效地检验IIG算法的有效性,与四种算法进行对比,设置了27种不同的测试机来检验数据配置,每种测试集都生成10个实例,总计270个实例。不同实例下的作业数量、工序数量和工序机器数量如表3所示。

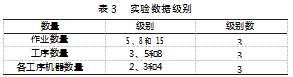
　　每个实例中相关的提前惩罚系数、拖期惩罚系数等参数采用随机生成的方式,具体如表4所示。

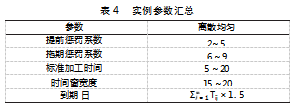
　　3.3性能指标

　　为评估所提出的多目标算法的性能,本小节采用RA性能指标。

　　帕累托最优解的比率(RA)[10]:计算解集A与帕累托优化解集P的共有解的数量除以P的解的数量的比率。由于没有问题的帕累托最佳解集,所以采用将四种算法找到的所有非支配解放入一个集合中,再对该集合进行非支配排序,最后得到一个非支配解集,即为帕累托优化解集P。注意,RA∈[0,1],并且该度量的量越大,表示解集A的质量越高。

　　3.4仿真分析

　　实例中每组数据都按照如“C5-2-2”方式表示,其表示含义为该组实例参数为5个作业、2道工序和每道工序有2台并行机器。所有对比算法都对每种测试参数的10个实例进行测试,统计每次的性能指标,最后求均值,结果如表5所示。

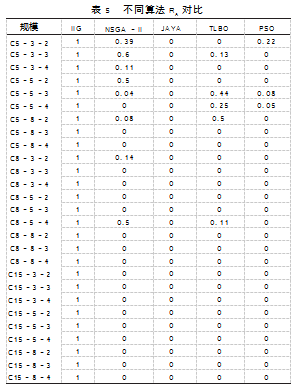
　　表5中加粗的数值为5种算法中的最优指标，可以看出其中IIG算法在两项优化指标中都能获得比其它4种算法更好的结果。对RA指标来说，IIG算法在270个实例中都能得到最大的结果，说明IIG算法能得到较优质量的解。

　　以实例参数为5个作业、3道处理阶段以及每阶段有3台并行机器为例，各算法所得帕累托解集对比如图1所示。

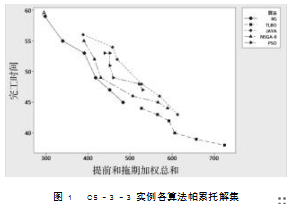
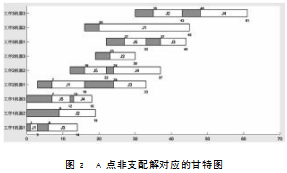
　　由图1可以看出，与其他4种算法对比，IIG算法所得的非支配解集最靠近帕累托前沿，从而可以说明本研究所提出的IIG算法对求解MOHFBSP问题具有找出较好的非支配解集的能力。为了说明算法的有效性，图2为图1中A点非支配解的甘特图。图中“J1”表示作业1，“工序1机器1”表示工序1机器1，灰色区域代表机器的加工准备时间。

　　4结束语

　　本文针对考虑交付时间窗和机器准备时间的混合流水车间调度问题，建立了该问题的数学模型，并基于IG算法提出改进算法(IIG)算法来解决该问题。最后通过实例对比发现，IIG算法在解决该类问题时比其他算法有优势。但是该算法还存在更科学改进的可能性，会在后续开展深入研究。

　　[参考文献]

　　[1]李颖俐，李新宇，高亮.混合流水车间调度问题研究综述[J].中国机械工程，2020，31(23):2798-2813+2828.

　　[2]Chen Z L，Lee C Y.Parallel machine scheduling with a common due window[J].European Journal of Operational Research，2002，136(3):512-527.

　　[3]Pan Q K，Gao L，Li X Y，et al.Effective metaheuristics for scheduling a hybrid flowshop with sequence-dependent setup times[J].Applied Mathematics and Computation，2017，303:89-112.

　　[4]田云娜，李冬妮，郑丹，等.一种基于时间窗的多阶段混合流水车间调度方法[J].机械工程学报，2016，52(16):185-196.

　   [5]Lin H T，Liao C J.A case study in a two-stage hybrid flow shop with setup time and dedicated machines[J].International Journal of Production Economics，2003，86(2):133-143.

　   [6]黄辉，李梦想，严永.考虑序列设置时间的混合流水车间多目标调度研究[J].运筹与管理，2020，29(12):215-221.

　　[7]陈水琳，郑建国.考虑准备时间的分布式混合零空闲置换流水车间调度问题[J/OL].计算机集成制造系统，1-322024-09-26].

　　[8]Pan，Q.K.，Ruiz，R.，Alfaro-Fernández，P.Iterated search methods for earliness and tardiness minimiz-ation in hybrid flowshops with due windows[J].Computers&OperationsResearch，2017(04):50-6

　　[9]王建华，邱荣根，王恒.基于多目标混合迭代贪婪算法的分布式混合流水车间调度问题[J/OL].计算机集成制造系统，1-19[2024-11-06].

　　[10]Saber R G，Ranjbar M.Minimizing the total tardiness and the total carbon emissions in the permutation flow shop scheduling problem[J].Computers&Operations Research，2022，138:105604.