【摘要】为践行“双碳”目标，倡导低碳出行，出现了可共享、可调度的电单车。针对系统中各站点库存不均衡的情况，研究了多仓库、多车型的再平衡路径优化问题，构建以最小化路径距离为目标的优化模型，并设计混合遗传算法进行求解。该算法结合遗传算法生成初始种群，使用模拟退火进行局部优化。最后，通过数值算例验证模型和算法的有效性，为共享电单车企业提供可行方案。

　　【关键词】多仓库；多车型；混合遗传算法；共享电单车；路径优化

　　１引言

　　从消费者的角度来看，电单车在速度、在不平坦地形下更省力以及长时间骑行的舒适性等方面比传统自行车更具优势[１]。对于运营商来说，尽管电单车在生产成本和运营成本方面都比传统自行车更高[２]，但电单车的骑行单价往往高于自行车，所以共享电单车能带来更可观的收入[３]。由于对消费者和运营商都有益处，共享电单车系统已发展到世界各地，如北美[４]和亚洲[５]等。截至２０１９年底，Ｇａｌａｔｏｕｌａｓ等[６]统计发现全球约有２９００多个正在运行的共享电单车系统。随着我国共享电单车规范管制标准逐步出台，各地政府共享电单车管制逐步放开，共享电单车行业呈现出良好的发展态势，对其调运路径规划问题的研究重要性也日益显现。

　　Ｆａｇｈｉｈ－Ｉｍａｎｉ等[７]提出，在共享电单车系统中，许多消费者的使用时间段和目标地点是一样的，从而导致供需时空失衡。例如，在人们从家骑车上班的早高峰时段，居民区闲置的电单车不足，而地铁站和商业区却因电单车数量过多而出现拥堵。这种时空不平衡导致了严重的问题，比如阻碍了消费者的出行，减少了平台的收入，占用了城市人行道。因此，共享电单车平台应在服务器内重新调配电单车，以平衡需求和供应。同时考虑到各个站点以及各个时间段的需求量可能有较大的不同，所以使用多车型进行再平衡能够更好地避免浪费车辆容量，降低成本。

　　通过对已有文献的梳理，发现目前对于共享电单车再平衡的研究，大部分只考虑单一仓库的共享电单车重新配置。而在实际生活中，考虑到货车最大里程限制，单仓库的共享电单车系统往往要配备更多的货车来完成再平衡需求，Ｌｉｕ等[８]提出部分国外的共享单车运营商如ＣｉｔｉＢｉｋｅ和ＬｉｍｅＢｉｋｅ等已经开始考虑在共享单车系统中增加仓库的数量。孙卓，李一鸣[９]设计了一种变邻域搜索算法来解决多仓库条件下的共享单车货车调配路线优化问题。多仓库能有效分散调度压力，避免单一仓库过度负荷，提升整体系统的运营效率。调度车辆的行驶距离也得以减少，从而降低燃料和人力运输成本。

　　参考之前的共享单车研究，使用卡车进行电单车再平衡任务是可行的，即卡车在低需求地区装载额外的电单车，然后将其卸载到高需求地区。同时，考虑到可拆卸电池技术已经普及，工作人员并不需要把整个车辆搬回仓库充电，只需要将耗尽的电池更换为新充电的电池。所以卡车还可以携带充满电的电池，从而解决充电问题。

　　因此，在本文中，我们考虑了一个带有可拆卸电单车电池的共享电单车系统，为共享电单车再平衡路径优化问题建立了数学模型，并设计混合遗传算法进行路径优化，与其他算法进行对比。

　　２问题描述及模型建立
      ２.１问题与假设

　　共享电单车系统有ｎ个节点，由ｎ１个仓库、ｎ２个停车点组成，ｎ＝ｎ１＋ｎ２。节点间的距离为ｄｉｊ(ｉ，ｊ∈１，…，ｎ)，每个运营站点ｉ(ｉ＝１，…，ｎ１)配备Ｖｉ辆电三轮和Ｔｉ辆轻型卡车用于各个停车点的车辆调运服务。公司在非交通高峰期对下一个交通高峰期节点车辆需求预测进行节点间车辆调运。令当前每个停车点ｉ(ｉ＝ｎ１＋１，…，ｎ)需要调出的车辆数为ｐｉ，需要调入的车辆数为ｄｉ，每个停车点或者仅有调出需求，或者仅有调入需求，即ｐｉ和ｄｉ必然有一个大于零一个等于零。为了方便模型构建，将全部电三轮和轻型卡车视为一个整体，令全部

　　运营站点中所配备的车辆总数为ｍ辆，使用０－１变量αｋｈ表示车辆ｋ(ｋ＝１，…，ｍ)是否停靠在站点ｈ(ｈ＝１，…，ｎ１)，车辆ｋ(ｋ＝１，…，ｍ)的最大装载量为Ｑｋ，单位里程运输成本为ｃｋ，每辆车的最大行驶里程为βｋ。该问题的目标是确定一种完成调运需求的总运营成本最小的车辆路径方案。

　　在服务区中，共享电单车的电池剩余容量是不同的。运营人员需定期调运共享电单车，例如，每隔４小时、每隔８小时、每天或每隔一晚。在调运时，工作人员将开着卡车前往，同时进行电池更换和调度操作。

　　当进行共享电单车调度时，假设对电量耗尽的共享电单车也进行电池更换，且不产生额外成本。这一假设成立的原因是，一旦对共享电单车进行了调度操作，更换其耗尽的电池所需的额外努力被认为是非常小的[１０]。每个工作人员都有时间预算来完成更换电池的任务，工作人员的卡车从仓库出发时会携带充满电的电池，而不是充电后的共享电单车。由于工作人员卡车上携带的电池体积很小，我们在这个问题中不对电池的总数量设定限制。

　　整个问题还满足如下假设:

　　①每个停车点只能由一辆车服务一次，

　　②一个停车点调出的车辆可以给多个需要调入车辆的停车点使用，

　　③一个需要调入车辆的停车点只能接受一个停车点调出的车辆，因为每个停车点只能接受一辆车服务一次，

　　④运输车辆最后需要返回其出发站点，

　　⑤全部停车点调出车辆总数量等于全部停车点调入车辆总数量，

　　⑥运输车从仓库空载出发，且空载返回。
       ２.２参数定义

　　本文的决策变量和中间变量定义如表１所示。

　　另外设计集合Ｖ＝{１，…，ｎ}表示全部节点，集合Ｋ＝{１，…，ｍ}表示全部车辆，集合Ｄ＝{１，…，ｎ１}表示全部仓库，集合Ｎ＝{ｎ１＋１，…，ｎ}表示全部停车点。

　　式(１)为模型目标函数，为全部车辆路径的总成本，式(２)约束每个停车区必须有一辆车对其进行服务，式(３)约束每个停车区进入和离开的车辆必须相同，式(４)约束每个仓库中出发的车辆必然是停靠在该仓库的车辆，式(５)约束车辆从某个仓库离开后也需要返回该仓库，式(６)约束车辆离开仓库时为空载状态，式(７)和(８)约束车辆在离开其路径中的第一个停车点时所装载的货品量等于当前停车点收集量与配送量之差，由于变量ｚ不小于０，该约束本质是实现车辆路径中的第一个停车点必然是具有调出需求的停车点，式(９)和(１０)约束车辆在经过前后两个停车点之间的弧时，车辆离开前一停车点的装载量与离开后一停车点装载量与其配载量和收集量之间的关系，式(１１)约束车辆在离开任何一个节点所装载的量不能超过所用车辆的最大容量，式(１２)约束车辆行驶总里程不能超出其最大行驶里程;式(13)约束车辆不能在停车点之间形成子回路;式(14)约束车辆不能在仓库间行驶;式(15)和(16)为决策变量非负整数约束和0-1约束。
       

　　3混合遗传算法设计

　　本文所研究的问题是典型的NP-hard问题,传统精确算法难以对该类问题进行快速求解,故选择启发式算法求解。遗传算法在应对约束、执行全局搜索以及维持算法稳定性方面表现出色,加之编程实现简便,已被广泛应用于多种场景下的车辆路径优化。但遗传算法在局部探索能力上有一定局限性,为解决此问题,本文创新性地提出将模拟退火算法融入遗传算法中,以形成混合遗传算法。采用遗传算法生成初始种群,随后利用模拟退火算法对每个个体进行细致的局部优化,以期寻找到更优的解。通过这一创新点加快算法的运算与收敛速度,有效防止算法陷入局部最优解,提高混合算法的效率。

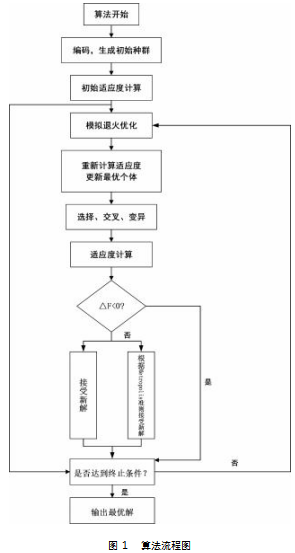
　　3.1编码与解码

　　采用直接编码方式:仓库节点数n1、客户节点数n2、车辆数m,编码为[n1+1,n1+n2]这n2个整数和m-1个分隔符0进行随机排列,第一个0之前为第一辆车所服务客户节点及其顺序,最后一个0之后为最后一辆车所服务客户节点及其顺序,第i(m-1>i>1)个0同其前一个0之间为第i辆车所服务客户节点及其顺序。当两个0前后相邻时表示有一个0所对应车辆不进行客户服务。以2个仓库、13个客户和3辆车的问题为例,其中三辆车所在仓库分别为1、1、2,一个编码可能如下:

      
　　解码后获得3辆车的路径依次为:
      

　　3.2种群初始化

　　随机生成初始化种群,每个个体是染色体,表示为节点的排列组合,即车辆行驶的路线。根据初始种群中每个个体(染色体)的路线,计算其适应度,即该路线的成本。记录当前最优解及其适应度。

　　3.3适应度计算

　　染色体的好坏用适应度值来衡量,适应度值代表最优解的优良程度,在遗传算法中,在交叉、变异等算子和约束条件下,个体形成适应度函数。本文的研究目标是最小化再平衡路径,对目标函数取倒数,实现最大值与最小值之间的转换,目标函数值越小,适应度函数值越大,适应性越强,个体就越优秀,反之个体越差。每条路径的适应度如式(17)所示。
       

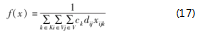
　　3.4集成模拟退火的遗传迭代

　　在每次外循环中,对每个个体先进行模拟退火再进行局部优化,尝试找到局部最优解。再对经过模拟退火优化的种群进行选择、交叉和变异,保持种群多样性,更新种群。记录和更新最优解,直到达到最大迭代次数或无改善次数阈值。

　　3.4.1模拟退火操作

　　把上一环节中选择的最优解进行两点逆序操作,选择两个交换点,反转它们之间的顺序,从而在每个内循环中生成新的邻域解。比较新解与当前解的适应度值,在本文中,适应值越小代表解越优秀,所以如果新解的适应度值低于当前解,接受新解;如果新解的适应度值高于当前解,根据Metropolis准则,计算被选择的概率如式(18)所示。
     

　　式(18)中,P是接受概率。Δf是当前解与新解之间的适应度差异,T是当前的温度,生成一个介于0和1之间的随机数r,如果r<P,则接受候选解,否则拒绝。

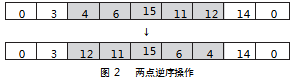
　　３.４.２遗传操作

　　本文采用精英选择策略进行个体选择，在每一代中，选择一些适应度最高的个体直接复制到下一代，不参与变异和交叉，以确保其优良基因能够保留到下一代。除了精英个体外，利用线性顺序交叉(ＬｉｎｅａｒＯｒｄｅｒＣｒｏｓｓｏｖｅｒ，ＬＯＸ)进行交叉操作，选择逆序变异(ＩｎｖｅｒｓｅＭｕｔａｔｉｏｎ)进行变异操作，从而保持种群的多样性。

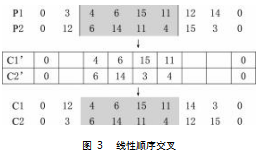
　　该操作的主要过程如下:首先，选择两个父代染色体进行交叉操作，在父代染色体中选择一个随机的交叉区间。其次，将一个父代染色体的交叉区间内的基因直接复制到子代染色体。再次，将另一个父代染色体中的剩余基因按顺序插入子代染色体中，保持顺序关系。在实际应用中，由于站点在配送路径中只能出现一次，因此，算法中的染色体元素不能重复，为此需要对交叉后的重复代码进行调整，直至每条染色体中的元素不相同。

　　在变异算法上，本文选择逆序变异，在染色体中选择两个随机位置，称为ｐｏｉｎｔ１和ｐｏｉｎｔ２。如果ｐｏｉｎｔ１大于ｐｏｉｎｔ２，则交换它们的值，将染色体中这两个点之间的所有基因顺序反转，以确保ｐｏｉｎｔ１小于ｐｏｉｎｔ２。同时，遗传过程中采用了最优解保留策略。适应值是评价染色体优劣的标准。

　　３.５终止条件

　　①达到最大外循环次数时，算法终止。

　　②如果在一定数量的外循环中没有找到更优的解，算法终止。

　　③达到最优解:如果在某一外循环中找到了一个比之前更优的解，算法终止。

　　４实例计算与结果分析
      ４.１算例设计

　　为了验证本文提出的改进遗传算法的有效性，本文结合共享单车实际运营情况，随机生成十二个算例来检验算法和ＣＰＬＥＸ模型的正确性以及车辆最大行驶距离对结果的影响，前六个小规模算例节点坐标在[０，１００]范围内随机生成，车辆最大装载量在[０，１０]之间，节点需求为[－１０，１０]范围内的整数。７－１２节点坐标在[０，５００]范围内随机生成，车辆最大装载量在[０，１００]之间，节点需求为[－１０，１０]范围内的整数。上述算法利用ＭＡＴＬＡＢ软件进行编程实现，仿真硬件环境为ＩｎｔｅｌＣＯＲＥｉ５/２.３ＧＨｚ/８.００ＧＢＤＤＲ３。十二个算例如表２所示:

　　数据文件两个数组的具体含义如下:

　　节点数据为节点基本信息二维数组，每一行为一个节点的编号、ｘ坐标、ｙ坐标和需求量，当需求量数值为正数时表示该节点车辆数量过多需要调出，当该数值为负数时表示该节点车辆数量不足需要调入，例如ｅｘ３＿２０＿５ａ算例中第四组数据[４，３０，５，－３]中第四个数字－３表示节点４需要调入３辆车，而第五组数据[５，３０，６５，３]中第四个数字３表示节点５需要调出３辆车。

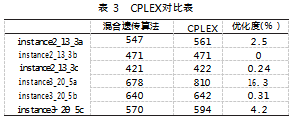
　　车辆信息为仓库运输车辆基本信息二维数组，每一行为一辆车的编号、所属仓库编号、最大装载量、单位里程成本和最大行驶距离，例如ｅｘ３＿２０＿５ａ算例中第二辆车的信息[２，１，１０，１，４００]表示该车属于仓库１、最大装载量为１０、单位里程成本为１以及最大行驶距离为４００。４.２与ＣＰＬＥＸ对比分析为验证算法的求解精度和运算效率，本文使用ＣＰＬＥＸ(Ｓｌｕｄｉｏ１２５１)求解数学模型并用于实验对比。针对六个小规模算例，分别进行算法求解和ＣＰＬＥＸ求解。求解结果如表３所示，结果代表本文算法在大部分情况下取得的最小值都小于ＣＰＬＥＸ的求解结果，显示出本文算法在求解复杂优化问题上的潜力，特别是在有复杂约束条件时。

　　4.3与已知算法对比试验

　　参数设计方面，本文取遗传算法种群规模为100，精英选择数量为3，交叉率为0.5，变异率为0.4，最大迭代次数为200。模拟退火初始温度为当前解的适应度值，冷却系数为0.985。为了对改进遗传算法进行测试，本文除应用本文算法求解外，还将与其他三种算法求解结果加以比较，每种算法均运行50次，得到距离最优值和平均值如表4所示。可以看出，在相同的参数设置下，本文提出的模拟遗传算法比其他的三种算法更优，能得到更好的求解结果。

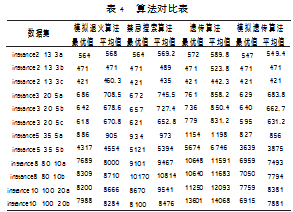
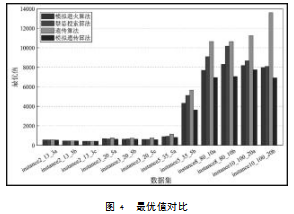
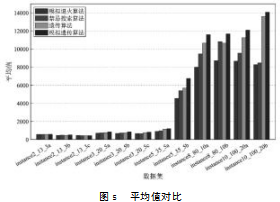
　　图4、图5分别为距离的最优值对比图和平均值对比图。从图中可以看出，在各数据集中，模拟遗传退火算法的平均值和最优值均小于其他算法，说明其有效地结合了模拟退火算法的全局搜索能力和遗传算法的局部搜索能力，更快地收敛到局部最优解。模拟退火算法和禁忌搜索算法的平均值相对较高，且禁忌搜索算法在13个节点的实例中相对稳定，但在20个以上节点的实例中波动较大。遗传算法单独使用时，性能和稳定性都较差，不建议单独使用，而是可以与其他算法结合使用。

　　5结束语

　　本文针对多仓库多车型的共享电单车系统中的再平衡问题和换电问题，建立了整数规划数学模型，并使用模拟遗传算法进行求解。将本文提出的模拟遗传算法与CPLEX整数规划求解结果进行对比，证明了算法的有效性，并将模拟遗传算法与其他三种启发式算法进行对比实验。结果显示，所提出的算法在多个测试实例中均表现出色，明显优于传统的优化算法。这说明本文提出的优化模型和混合启发式算法可以有效降低路径成本，提高工作效率。后续研究可以优化算法参数，探讨其他混合启发式算法的可能性，并扩大算例规模，以进一步验证算法的实用性和鲁棒性。

　　[参考文献]

　　[1]Chen Z，Hu Y，Li J，et al.Optimal deployment of electric bicycle sharing stations:Model formulation and solution technique[J].Networks and Spatial Economics，2020，20(1):99-136.

　　[2]Cherry C R，Worley S，Jordan D.Electric Bike Sharing System Requirements and Operational Concepts[C]//Transportation Research Board Meeting.2011.

　　[3]Zhu S.Optimal fleet deployment strategy:Model the effect of shared e-bikes on bike-sharing system[J].Journal of Advanced Transportation，2021(2):6678637.1-6678637.12.

　　[4]Brian，Casey，Langford，et al.North America,s First E-Bikeshare:A Year of Experience[J].Transportation Research Record，2018(11):120-128.

　　[5]Cherry C，Yang H，Jones L R，et al.Dynamics of electric bike ownership and use in Kunming China[J].Transport Policy，2016(01):127-135.

　　[6]Galatoulas N F，Genikomsakis K N，Ioakimidis C S.Spatio-temporal trends of e-bike sharing system deployment:A review in Europe，North America and Asia[J]. Sustainability，2020，12:4611.

　　[7]Faghih-Imani A，Hampshire R，Marla L，et al.An empirical analysis of bike sharing usage and rebalancing:Evidence from Barcelona and Seville[J].Social Science Electronic Publishing，2017，97:177-191.

　　[8]Liu Y，Szeto W Y，Ho S C.A static free-floating bike repositioning problem with multiple heterogeneous vehicles，multiple depots，and multiple visits[J].Transportation Research Part C:Emerging Technologies，2018，92:208

　　-242.

　　[9]孙卓，李一鸣.考虑多仓库的共享单车重新配置问题研究[J].运筹与管理，2021，30(001):121-129.

　　[10]Lee G，Lee J S，Park K S，et al.Battery swapping，vehicle rebalancing，and staff routing for electric scooter sharing systems[J].Transportation Research Part E:Logistics and Transportation Review，2024，186.

　　[11]张雨婷，干宏程.旧衣物回收的快时尚服装门店同时送取货车辆路径优化研究[J].物流工程与管理，2023，45(9):50-55.

　　[12]刘喜梅，潘立军.一种求解共享单车再平衡问题的遗传算法[J].计算机工程，2019，45(10):308-313.

　　[13]潘立军，符卓，刘喜梅.共享单车再平衡问题及其容差插入启发式算法[J].运筹与管理，2019，28(10):26-32.