【摘要】与传统的制造业调度问题相比，MRO(Maintenance，Repair and Overhaul，即航空维修，包括飞机维护、修理和翻修)系统面临更多的不确定性和复杂性，如拆分－修理－组装的三级结构、待维修件质量水平的不确定、物料匹配需求以及不确定工艺路线和工时。文中针对MRO调度问题建立以最小化期望权重延误时间为目标的混合整数线性规划模型，然而，使用传统的优化方法很难对此类NP－hard问题求得最优解，于是提出一种基于嵌套分割(NP)算法框架的混合算法NP/NEH/OCBA对该问题进行求解，最后，通过基于实际背景的算例验证了模型的可行性并对比分析了NP/NEH/OCBA算法与其它相似算法的优势。

　　【关键词】航空维修;不确定工艺路线;不确定工时;嵌套分割;仿真优化

　　1引言

　　航空维修业是航空产业链条中的重要一环。MRO是航空维修的简称，即飞机维护、修理和翻修(Maintenance，Repair and Overhaul)，其定义和解释可追溯到美国联邦航空管理条例FAR和中国民用航空管理条例。

　　MRO企业运营除了受自身因素影响以外，还与原始设备制造商、航空公司等相关。MRO企业面临诸多不确定因素，航空公司对维修形式的决策往往影响企业对维修过程中维修工作量的计划，使得维修内容产生波动。有数据显示［1］，在维修过程中，大约50%的MRO公司面临着40%－59%的不确定的维修内容。图1形象地展示只有随着维修过程的进行［2］，维修工作量信息才能逐渐被完全确定，这使得维修过程管理更具复杂性和挑战性。

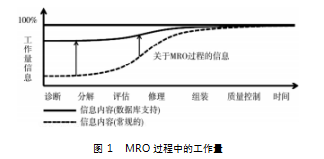
　　计划调度是航空部件维修管理的主线，如何在不确定场景下有效地解决MRO企业的调度问题，在强化计划纲领性作用，提高作业效率，最大化资源利用，以及减少库存占用和满足客户交付需求等方面具有重要意义。MRO企业是再制造工业的重要组成部分，然而，一些复杂的特点使得MRO计划与调度问题与传统制造业有很大不同，例如:拆分－修理－组装的三级结构、待维修件质量水平的不确定、物料匹配需求以及不确定工艺路线和工时［3］。作为一种新的研究领域，MRO调度问题的复杂性和不确定性引起了学术界的广泛关注。

　　2国内外研究现状

　　Guide等的多篇文章［4－6］中对MRO问题及其复杂特点进行描述和总结，其提出再制造的一般过程，如图2所示，并将再制造过程划分为三个阶段:分解(Disassembly)、再制造(Remanufacturing)和组装(Reassembly)，同时指出，MRO系统比传统制造业系统面临更多的不确定性和复杂性，针对MRO系统的生产计划和调度进行研究相当有必要，然而，这些复杂的特点使得MRO系统的生产计划和调度很难进行。

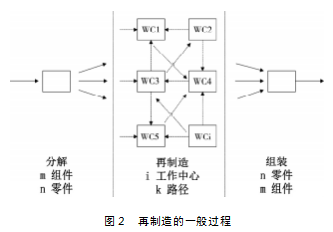
　　仿真优化是一种适合解决含有不确定性调度问题的有效方法。Christoph等［1］通过建立仿真模型，将准时交货率、在制品率、利用率以及生产周期作为衡量标准，同时发现FIFO/Slack和ESD/Slack的规则组合会取得更好的效果。Chen等［7］提出的OCBA技术可以通过合理分配计算量来取得更大的正确选择概率，或者在实现一定的正确选择概率的基础上大大减少仿真计算量。Xu等［8］提出的MO2TOS算法框架是一种新的灵活的优化方法，但是比较耗时。文献［9－10］在验证MO2TOS算法的前提下也对该方法进行优化，其中Molina-Crist6bal等［9］将多种复杂算法嵌套在MO2TOS框架内，在低精度模型求解时运用一种全局搜索算法以提高效率。郝春锋等［3］在对航空维修企业调度问题国内外研究现状进行详细分析的基础上，建立以最小化期望权重延误时间为目标的混合整数线性规划模型，因为该问题是NP－hard问题，通过使用传统的优化方法很难求得最优解，他们提出基于多精度仿真模型的MO2TOS算法对该问题进行求解，将低精度仿真模型应用到MO2TOS算法框架的OT阶段，并用OCBA方法进行抽样。通过大量算例证明了MO2TOS算法框架在计算MRO调度问题方面的高效性。然而，当问题规模继续增大时，由于解空间巨大，此时MO2TOS算法将不再适合求解该问题。

　　丁金想等［11］针对MRO调度问题的复杂性和不确定性构建仿真模型，并提出三种启发式算法，分别是调度规则、NEH算法和GA算法，其中NEH算法属于构造型启发式算法，GA属于改进型启发式算法。然后对这三种启发式算法的计算流程进行详细介绍，最后给出若干计算算例，分别使用三种启发式算法进行计算，并将计算结果进行展示和对比分析。通过大量算例得出结论:调度规则算法计算时间快，但计算结果较差，GA算法的计算结果最好，但是非常耗时，适用于对解的质量要求很高的情况，而NEH算法在计算时间和求解质量方面居于调度规则和GA算法之间。

　　本研究是在以上研究基础上开展的(其中，对MRO调度问题的描述和仿真模型与作者之前文章中保持不变)，通过基于NP框架的仿真优化方法解决大规模问题情况下的MRO调度问题。

　　3 MRO调度问题建模

　　3．1 MRO问题描述

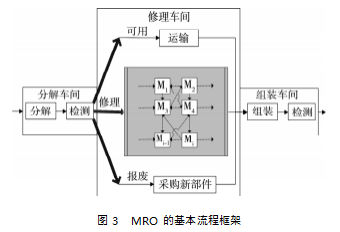
　　MRO的基本流程框架如图3所示(其中M表示机器)，一般包含分解、修理和组装三个车间。

　　在分解车间，根据BOM结构，待维修件首先被分解成子部件，每个子部件经过检测来确定维修内容，子部件的损坏程度不同，维修工艺路线也不相同，因此，每个子部件在修理车间的实际工艺路线只有在完成分解和检测工序之后才能被确定。为了不失一般性，我们以此为模型，研究MRO企业的调度问题，显然待维修件在分解车间分解工序的作业顺序、子部件在修理车间可能经过的相关工序上修理的作业顺序、子部件在组装车间组装工序的作业顺序是决策变量。最小化期望权重延误时间之和是此类调度问题的优化目标。

　　3．2 MRO调度问题的仿真模型

　　MRO问题结构复杂，不确定性因素多，比如待维修件的到达时间不确定，子部件在修理工序上的加工时间不确定，子部件的维修工艺路线也存在不确定性等。作者结合在一家MRO企业的咨询项目经历，对所研究的这类问题做出以下假设:

　　·分解车间和组装车间均只包含一个工序，并各由一台机器完成作业;

　　·修理车间包含多个工序，每个工序各由一台机器完成作业，每个被拆分的子部件修理路线是不确定的，经过的修理工序顺序和种类不同。

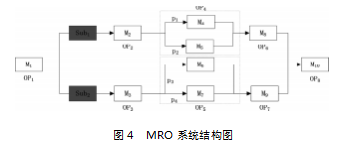
　　如图4所示，OP1和OP8分别代表分解、组装车间工序，OP2至OP7表示修理车间工序。假设待维修件数量是n，OP4和OP5各拥有两个不同的机器，拆分后的子部件按一定概率执行相关机器作业，通过这个处理来体现出维修路线的不确定性。根据实际MRO企业的咨询经验来看，并不是所有工序的加工时间都是不确定的，因此，我们只假设OP6和OP7的加工时间不确定，其他工序加工时间为确定值。首先，我们基于C++建立以最小化期望权重延误时间为目标的仿真模型。

　　4基于NP框架和仿真的MRO调度问题算法研究

　　4．1嵌套分割(NP)算法

　　嵌套分割(Nested Partitions)算法是由Shi，Ólafsson［12］提出的一种新型全局优化算法，并已经被证明能够以概率1收敛于全局最优解。该算法可以有效地把全局搜索和局部寻优结合在一起，具有开放性、并行性、全局性和易操作性等突出优点，能够高效解决许多确定型和随机型的大规模优化问题。此外，嵌套分割算法可以与其它优化方法有机结合，兼收其它方法的优点，如Shi等［13］将NP算法与GA算法结合，得到了比GA算法更好的结果，Shi［14］将NP算法、序优化和OCBA(Optimal Computing Budget Allocation)技术结合，得到的新算法被证明在求解大规模随机离散优化问题时更加高效，此外，NP算法在TSP问题、生产调度等领域都取得了显著的效果［15－17］。虽然NP算法具有广阔的应用前景，但国内对这种方法的研究还十分有限［17－18］。

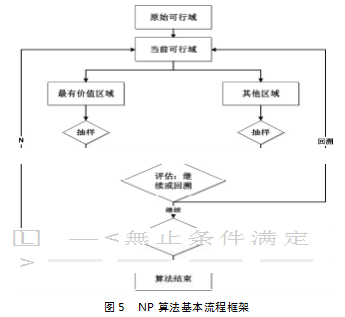
　　NP算法的基本结构框架如图5所示。

　　在NP算法的每次迭代过程中，我们假设存在一个区域σ⊆Θ,并称这个区域为“最有价值区域”，其中Θ表示整个问题的可行域。首先将最有价值区域划分成M个子区域，并且将除区域σ以外的所有区域当作是一个补集区域。在每次迭代过程中，我们因此有覆盖整个可行域的M+1个互不相交的子区域。针对M+1个区域的每个子区域，通过随机抽样机制进行抽样，然后根据样本点，使用评价函数去估计每个子区域的“价值指数”。“价值指数”的大小决定接下来哪个子区域将变成新的“最有价值区域”，如果“价值指数”最大的区域是M个子区域中的一个，则该子区域是新的“最有价值区域”;如果“价值指数”最大的区域是补集区域，则NP算法回溯到一个更大的区域。为了选择这个更大的区域，我们需要使用一个固定的回溯规则。最后，这个新的“最有价值区域”按照上面的形式继续被分割。NP算法可以划分为四步，基本流程如下。

　　①分割。

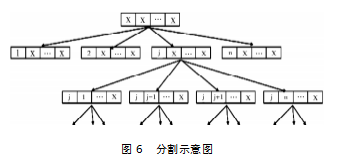
　　搜索空间在搜索过程中被依次分割。在每一个迭代步骤中存在一个最有价值的区域(Most Promising Region)，此区域会被进一步划分为M个子区域:σ1，σ2，…,σM以及一个补集区域σM+1。补集区域包含除了最有价值区域之外的所有区域。因本文模型是以寻找最优顺序为目标，即决策变量是n个待维修件的顺序，其基本划分示意图如图6所示。

　　②随机抽样。

　　在每一个迭代步骤中，使用随机抽样方法对每一个子区

　　域σj进行抽样，并产生指定数量的样本点，称为x，i=1，2，

　　…,Nj。

　　③估计价值指数。

　　每个子区域最好的采样点被称为子区域的“价值指数”，其被作为产生下一个最有价值区域的基础。

　　I(σj)=i∈{1m，2 n，Nj}f(x)，j=1，2，…,M+1，

　　j*=j∈{1，2a，rg，M+1}minI(σj)

　　④回溯。

　　如果价值指数指向某个特定的子区域，则此区域被称为下一个最有价值区域。如果价值指数指向补集区域σM+1，则算法回溯到前一个最有价值区域。

　　鉴于NP方法的独特性质，在仿真优化的研究中选择NP方法作为基础架构具有明显优势。首先，NP方法几乎没有对解空间做任何假设，这使得很多数学工具都可以被使用;其次，在每一个迭代步骤中，NP方法都会从子区域中提取大量的用于估计的采样点，这些采样点可以被灵活地应用于各种统计分析;再次，NP方法与其他基于模型的方法在概念上有所类似，都是选取最优的区域，这有助于将基于NP的方法向其它方面推广;最后，NP方法的结构性强，非常适用于做算法改进与渐进性分析。

　　NP算法只是一个优化框架，实际应用中我们可以将其他优化算法或技术整合到NP框架中，比如，分割思想与现有的并行技术结合，将每个区域进行独立计算，可以进一步缩短计算时间;NP算法同样可以和先进的抽样技术、局部搜索算法等结合以进一步提升抽样效率，克服NP算法效率低的缺点。因为在算法中，如果当前“最有价值区域”只含有一个解，而且这个解的“价值指数”比另一个区域几乎所有解都要好，但不是全部。这种情况下，NP算法可能要消耗很长时间才能回溯到另一个区域。

　　4．2基于NP框架的混合算法

　　本文针对NP算法框架可以和先进的抽样技术、局部搜索算法结合的特点，以及丁金想等［12］得出的NEH算法在计算时间和求解质量方面居于调度规则和GA之间的结论，提出一种新的混合算法。这种混合算法是将NEH算法和NP算法结合，让NEH作为一种局部搜索算法在NP的每个子区域中寻找较优解，并应用先进的OCBA技术分配仿真预算和选择最优价值区域，其被称为NP/NEH/OCBA算法。

　　对于NP/NEH/OCBA混合算法，当我们将NEH算法整合到NP框架中时，首先使用随机抽样方法在每个子区域内抽取若干样本点，然后使用OCBA技术在这些样本点中寻找最优样本点，最后，将寻找到的最优样本点作为NEH算法的初始解，使用NEH算法进行局部寻优，NEH算法得到的解即认为是该子区域最优解，并以此解计算该区域的价值指数。NP框架中的分割和回溯步骤不变。可见，这种混合算法充分利用并保存两种算法的优点，如NP算法的全局思想和NEH算法强大的局部搜索能力。

　　在NP/NEH/OCBA算法的第k次迭代过程中，我们假设存在一个区域σ(k)为“最有价值区域”，其中Θ表示整个问题的可行域。初始化时，因为我们不知道哪个子区域为“最有价值区域”，因此σ(k)⊆Θ。第一步，将当前最有价值区域划分成M个子区域，并且将除区域σ以外的所有区域认为是一个补集区域，可见，在算法的每一步我们都考虑到了整个可行域。在每次迭代过程中，我们有覆盖整个可行域的M+1个互不相交的子区域。第二步，针对M+1个区域的每个子区域，通过随机抽样机制进行抽样，获得初始样本集，针对每个区域的初始样本集，使用OCBA技术在这些样本点中寻找最优样本点。第三步，将寻找到的最优样本点作为NEH算法的初始解，使用NEH算法进行局部寻优，NEH算法得到的解即认为是该子区域最优解，并以此解计算该区域的价值指数。第四步，应用序优化和OCBA技术寻找所有价值指数中表现最好的个体所属区域，如果“价值指数”最大的区域是M个子区域中的一个，则该子区域是新的“最有价值区域”;如果“价值指数”最大的区域是补集区域，则NP算法回溯到一个更大的区域。为了选择这个更大的区域，我们需要使用一个固定的回溯规则。最后，这个新的“最有价值区域”按照上面形式继续被分割直到当前“最有价值区域”不能被继续分割。

　　NP/NEH/OCBA算法的基本流程如下:

　　步骤0:初始化。设置k=0，σ(k)=Θ。

　　步骤1:分割。如果|σ(k)|＞1，将当前最有价值区域σ(k)划分成Mσ(k)个子区域:

　　σ1(k)，σ2(k)，…,σMσ(k)(k)

　　如果σ(k)≠Θ,将除σ(k)以外的所有区域整合成一个区域，成为σ(k)的补集区域，σMσ(k)+1(k)=Θσ(k)，可见Mσ(k)与σ和k都有关系。

　　步骤2:抽样。如果|σ(k)|＞1，使用随机抽样方法在每个区域σj(k)内得到大小为Nj的样本点集合，j=1，2，…,Mσ(k)+1。记:

　　Dσj(k)={θj1，θj2，…,θNj}，j=1，2，…,Mσ(k)+1

　　对于抽取的每个子区域的样本点集合Dσj(k)，使用OCBA技术寻找出较优样本点，记为θσj(k)。

　　步骤3:NEH搜索。将子区域σj(k)中的较优样本点θσj(k)作为初始解，分别使用NEH搜索获得最优样本点，记为θs(tk)。

　　步骤4:使用序优化和OCBA技术确定新的最有价值区域。应用序优化和OCBA技术找到表现最好的个体所属区域，并将该区域设为新的最优价值区域。

　　本文模型中，J(θ)是目标函数，J(θ)=E[ΣiλiTi］，假设I表示价值指数，则对于子区域σj(k)

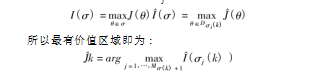
　　步骤5:继续分割或回溯。如果在步骤4中有不止一个区域的价值指数相同，则使用随机选择的方式确定其中一个。如果“价值指数”最大的区域是Mσ(k)个子区域中的一个，则该子区域是新的“最有价值区域”;如果“价值指数”最大的区域是补集区域，则NP算法回溯到一个更大的区域。设置k=k+1，转到步骤1。

　　在NP/NEH/OCBA混合算法中，步骤2和步骤4是非常耗时的，而序优化和OCBA技术的使用，使整个算法的效率得到很大提升。

　　4．3算例设计与结果分析

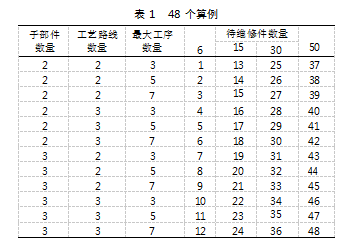
　　为了验证本章提出的混合算法NP/NEH/OCBA是否比纯启发式算法NEH表现更好，本节设计新的算例进行验证，算例设计以丁金想等［12］的文章算例背景为基础，除每个待维修件的延迟权重(l值)修改为从U(1，5)中随机产生以外，其他参数保持一致。根据这些参数，我们可以随机产生48个算例，如表1所示。为了表述方便，对其进行编号，并且用符号G1表示小规模问题(订单数是6或15)，G2表示中等规模问题(订单数是30)，G3表示大规模问题(订单数是50)。本节使用相对Gap值比较不同算法的表现。

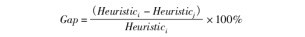
　　其中，Heuristici表示第i种启发式算法计算得到的目标函数值。

　　为了比较不同算法的计算效果，我们计算每个目标函数值的均值和方差，最优性比较是基于假设检验，下文所有对比结果的置信度均为95%。

　　本节所有算法程序都使用C++编码，并在英特尔酷睿i3，主频3．40GHz的CPU和4．00GB内存的*位win7电脑上进行运算。对于每个解，我们将仿真次数设置为1000，以消除噪音获得稳定目标函数值。

　　不同算法的计算结果以及计算时间如表2、表3和表4所示，其中混合算法NP/NEH/OCBA的终止条件是当前最有价值区域只包含一个解或计算时间达到给定的时间限制，这个时间限制点是以GA运行时间来设定的，GA算法的终止条件是迭代次数达到3*n(其中n为待维修件数量)。对于所有算例，表中给出所有算法得到的目标函数值，Gap代表混合NP/NEH/OCBA算法和纯NEH算法的相对表现。

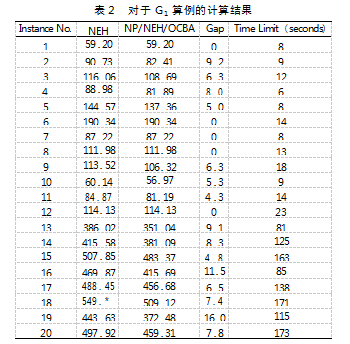
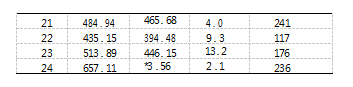
　　表2展示的是针对小规模问题G1，不同算法给出的计算结果和对比。从表中可以看出，对于所有算例，Gap的值都大于或等于0，这就意味着对于同一算例，当把NEH启发式算法整合到NP算法框架后，新的混合算法得到的解至少不比相应的纯启发式算法差。观察表中Gap的值可以发现，小部分的Gap值等于0，这意味着在给定的计算时间内，NEH算法和混合NP/NEH/OCBA算法都找到了相同的解或者是找到的解没有统计意义上的明显差异。

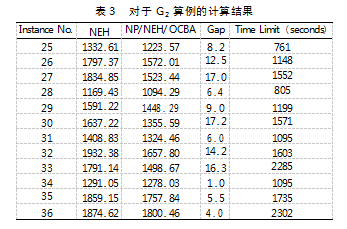
　　表3展示的是针对中等规模问题G2，不同算法给出的计算结果和对比。对于中等规模问题G2，可以直观发现所有Gap的值都大于0，这一结论强烈地说明了，随着问题规模的增大，新的混合NP/NEH/OCBA算法可以得到更好的调度结果。此外，从表3中可以发现，在给定的计算时间内，NP/NEH/OCBA算法与纯NEH算法相比，提高量高达17．2%。

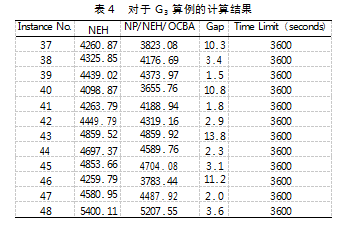
　　表4展示的是针对大规模问题G3，不同算法给出的计算结果和对比。从表中可以看出，所有Gap的值都大于0，这说明随着问题规模的继续扩大，新的混合NP/NEH/OCBA算法依旧可以得出比纯NEH启发式算法更好的解。同样，从表中可以发现，在给定的计算时间内，NP/NEH/OCBA算法与纯NEH算法相比，最大的提高量达到13．8%。但该值小于对于中等规模问题G2得到的最大提高量，这是因为，当问题规模变大时，新的混合算法NP/NEH/OCBA计算时间远超过3600s，而此时将计算时间控制在3600s限制了新的混合算法寻优。

　　5结论

　　本文首先介绍嵌套分割(NP)算法的基本思想以及序优化和OCBA技术的基本含义。因为NP算法只是一个优化框架，在实际应用中NP框架可以和其他优化算法或技术进行整合，基于前人对NEH启发式算法进行的介绍和对比分析发现，NEH算法在计算时间和求解质量方面居于调度规则和GA之间。本文将NEH启发式算法整合到嵌套分割算法框架的基本思路，并将序优化和OCBA技术恰当地应用到优化框架中，提出一种基于嵌套分割算法的混合算法，即NP/NEH/OCBA算法。为了验证本文提出的新的混合算法NP/NEH/OCBA是否比纯启发式算法NEH表现更好，本文以丁金想等［12］的文章算例背景为基础设计新的算例进行验证。

　　通过算例计算，当把NEH启发式算法整合到NP算法框架后，新的混合算法得到的解至少不比相应的纯启发式算法差。对于大规模问题，这种优势将更加明显。此外，我们还可以得出结论，对于小规模和中等规模问题，因为计算时间快等优点，NEH算法适合作为NP框架中的局部搜索方法，而当问题规模增大时，如果控制新的混合算法NP/NEH/OCBA的计算时间，混合算法的寻优能力将被限制。

　　NP算法只是一个优化框架，很多高效的局部或全局搜索算法都可以被有机地整合到NP框架中。因为考虑到NEH算法效率高的特点，所以本文只是尝试将这种启发式算法整合到NP框架中以便进一步提高算法能力。如何基于NP框架来发展系统的方法去整合其他启发式算法是一个有价值的研究方向。

　　［参考文献］

　　［1］Christoph Reményi，Stephan Staudacher．Systematic simulation based approach for the identification and implementation of a scheduling rule in the aircraft engine maintenance．International Journal of Production Economics，2014，147:94－107.

　　［2］Eickemeyer S C，Nyhuis P．Capacity planning and coordination with fuzzy load information［J］．Business Review，2010，16(1):259－2*.

　　［3］郝春锋，丁金想，栾世超．基于MO2TOS算法的航空维修业调度问题研究［J］．工业工程，2017，6(20):56－*.

　　［4］Guide Jr V D R,Srivastava R,Kraus M E．Product structure complexity and scheduling of operations in recoverable manufacturing［J］．International Journal of Production Research，1997，35(11):3179－3200.

　　［5］Guide V D R,Jayaraman V，Srivastava R.Production planning and control for remanufacturing:A state－of－the-art survey［J］.Robotics and Computer－Integrated Manufacturing，1999，15(3):221－230.

　　［6］Guide V D R.Production planning and control for remanufacturing:Industry practice and research needs［J］.Journal of Operations Management，2000，18(4):467-483.

　　［7］C．－H．Chen，J．Lin，E．Yücesan，S．E．Chick．Simulation budget allocation for further enhancing the efficiency of ordinal optimization［J］．Discrete Event Dynamic Systems，2000，10(3):251－270.

　　［8］J．Xu，S．Zhang，E．Huang，C．Chen，L．Lee，N．Celik．Mo2tos:Multi－fidelity optimization with ordinal transformation and optimal sampling［J］．Asia－Pacific Journal of Operational Research，2016，33(03):1608－1620.

　　［9］A．Molina－Crist6bal，P.R.Palmer，B．A．Skinner，G．T.Parks．Multi－fidelity simulation modelling in optimization of asubmarine propulsion system［C］．2010，IEEE Vehicle Power and Propulsion Conference(VPPC)，Lille，France，2010:1－6.

　　［10］V．Balabanov，G．Venter．Multi－fidelity optimization with high－fidelity analysis and low－fidelity gradients［C］．In 10th AIAA/ISSMO Multidisciplinary Analysis and Optim-ization Conference，Albany，New York，USA，2004－8－30.

　　［11］丁金想，栾世超，石晓磊，连福诗．基于仿真优化的MRO调度问题研究［J］．物流工程与管理，2019，41(5):6.

　　［12］Shi L，Ólafsson S．Nested partitions method for global optimization［J］．Operations Research，2000，48(3):390-407.

　　［13］Shi L，Ólafsson S，Chen Q．A new hybrid optimization algorithm［J］．Computers＆Industrial Engineering，1999，36(2):409－426.

　　［14］Shi L．A new algorithm for stochastic discrete resource allocation optimization［J］．Discrete Event Dynamic Systems，2000，10(3):271－294.

　　［15］Shi L，Ólafsson S，Sun N．New parallel randomized algorithms for the traveling salesman problem［J］.Computers＆Operations Research，1999，26(4):371-394.

　　［16］Ólafsson S，Shi L．A method for scheduling in parallel manufacturing systems with flexible resources［J］．IIE Transactions，2000，32(2):135－146.

　　［17］刘昌军，苏琴，卫军胡．嵌套分割算法在旅行商问题上的应用［J］．系统仿真学报，2008，20(24):6858－6861.

　　［18］张林刚，严广乐，路晓伟．嵌套分割算法:一种新的并行随机优化算法［J］．计算机应用研究，2007，24(6):79-81.