【摘要】针对当前车辆路径规划算法存在的车辆满载率低、车辆路径求解时间长、车辆配送成本高的问题，文中设计了考虑客户等级划分的车辆路径遗传算法求解过程。在描述车辆路径相关问题和函数的基础上，给出相关假设和约束条件，确定目标函数并考虑客户等级划分，然后构建时间窗车辆路径模型。采用遗传算法，通过染色体编码生成初始种群，再通过选择、交叉以及变异输出最优解，从而求解时间窗车辆路径。实验结果表明：该方法能够有效提升车辆满载率，并缩短求解时间、降低配送成本。

　　【关键词】车辆路径问题；客户等级划分；遗传算法；适应度函数；变异概率

　　1引言

　　作为物流系统中最重要的功能和环节之一，配送过程发挥着举足轻重的作用[1-2]。在物流成本中，由配送产生的运输费用所占比例较大，配送费用过高，造成物流总成本的增加。为了实现对物流成本的有效控制，达到降低成本的目的，需要对物流配送环节进行有效的规划[3]。目前，通过规划车辆路径使得运输成本降低已经成为该领域的热点问题。

　　文献[4]通过从客户代表处转移知识实现更快的车辆路径选择。该方法通过学习新的客户表示来捕获先前优化的隐藏特征，客户表示可以在车辆路径问题之间传递并作为先验知识，从而对目标车辆路径问题中的优化产生偏差。而车辆路径问题的知识转移贯穿于整个优化搜索过程，能够有效指导路径优化过程。文献[5]中利用基于图的模糊进化算法求解两级车辆路径问题。该方法利用群体演化的优势，避免过多适应度评估。通过基于图的模糊指派过程从父个体的指派图中产生子代，并利用模糊局部搜索过程进一步改进子代，从而获得最优路径。然而在实际应用中发现，上述方法存在车辆满载率低、求解时间长、配送总成本高的问题。

　　针对上述问题，本研究在描述车辆路径问题和函数的基础上设定假设和约束条件，考虑客户等级划分并建立车辆路径模型。然后采用遗传算法求解该模型，使车辆满载率得以提升，并有效降低了求解时间和配送成本。

　　2考虑客户等级划分的车辆路径模型构建

　　2.1车辆路径问题描述

　　车辆路径问题是指单场封闭车辆路径问题[6]。描述车辆路径问题如下：

　　设置一个配送中心，有许多运输车辆能够实施调度，运输车辆需要派送多个客户节点的货物。设置对货物的需求和各个客户节点的位置，并且不同服务时间窗口限制的各个客户，都规定其必须有且仅有一辆汽车提供服务，运输车辆完成配送任务后，必须返回配送中心。假设以上的描述为已知，最小化运输总成本的同时，最大化反映客户满意的潜力值之和。

　　考虑客户等级划分的时间窗车辆路径问题的优化目标可具体描述如下：

　　①最低化总运输成本，主要由车辆固定成本、行驶距离变更成本以及违反时间窗处罚成本等构成[7]。

　　②最大化客户整体潜在价值，客户等级越高，其潜在的价值能够被挖掘的越大。

　　2.2车辆路径相关假设

　　本文的研究重点主要是考虑客户等级划分的时间窗车辆路径模型，为减少计算量，降低复杂度，设置下列假设为：

　　①已知运输中心以及客户位置；

　　②已知客户需求，且不会发生变化；

　　③仅考虑车辆行驶燃油消耗量成本；

　　④在运输过程中，所有车辆都保持相同的速度行驶；

　　⑤假定车辆从0时刻在配送中心发出；

　　⑥如果在客户规定时间窗内，运输车辆完成服务任务，那么客户将十分满意；

　　⑦若客户对客户传播信息的接受度取决于客户规模，则大客户大于小客户；

　　⑧车辆故障、交通拥挤和天气变化等不可抗拒因素在运输过程中不予考虑。

　　2.3客户等级划分

　　由于配送资源是有限的，因此，在配送需求的高峰期难以出现同一时间向多个客户一起配送的情况。因为有限的配送资源，促使在配送高峰时期，不能同时间向多个客户进行配送。所以以企业中客户创造的利润为依据，采用ABC分类法，根据不同的重要程度，划分物流客户[8]。本文将普通客户划分为一般和适当客户，构造两大类模型，即普通和VIP客户，以此来简化模型。在规划路径时，首先分类配送客户。根据客户对已知敏感性的配送时间可知，配送时间要求越高，则时间敏感性系数越高。客户等级划分与时间窗的关系如图1所示。

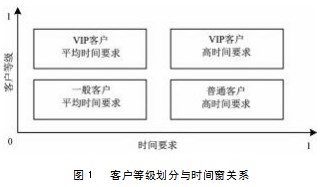
　　根据图1可知，将客户等级划分为：VIP客户、普通客户、一般客户，将时间窗关系划分为高时间要求与平均时间要求[9]。在这四种客户中，优先考虑VIP与时间要求高的客户，然后再考虑另外三种客户服务。针对车辆运输问题，客户存在一个期望的时间和一个可以接受的时间。如果在客户所期望的时间内配送，那么满意度将达到最高。反之，如果超过客户所期望的时间配送，那么满意度会降低，且随着时间敏感性的变化而变化。针对不同时段的客户满意度如何衡量，提出了模糊的预约时间。

　　2.4相关函数描述

　　2.4.1客户潜在价值函数

　　本文运用连续线性函数来表示客户满意度变化的情况，应用模糊数学函数来表示客户可以接受的时间。客户满意度与配送时间关系如图2所示。

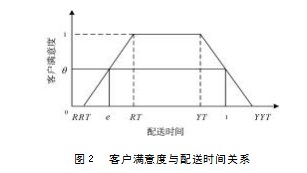
　　将配送时间隶属度函数设置为客户q所期望的时间的满意度W(Eq)表示为：

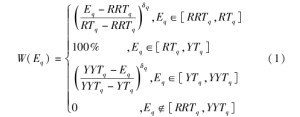
　　式(1)中，[RRTq、YYTq]代表客户期望运输时间窗，[RTq,YTq]代表客户可以接受运输时间窗，δq代表客户配送时间敏感性系数，Eq代表配送车辆抵达客户位置所用时间。

　　2.4.2车辆惩罚成本函数

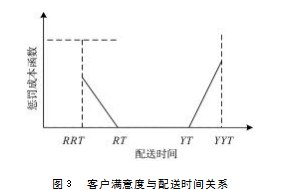
　　若车辆不能在期望运输时间窗内到达，由于车辆配送提前或延迟的原因，使客户计划受到影响，造成一定损失。因此，客户需要将此损失转嫁给运输车辆，并且承担一定的罚款，其拖延时间越长，处罚费用就越大，从而增大惩罚成本函数[10]。若车辆不能在可接受运输时间窗内到达，由于此时客户与期望运输时间窗距离过大，对客户提供配送已经无任何意义，因此，为避免提供客户无意义服务，必须在客户期望的配送时间窗内进行车辆运输。惩罚成本函数与配送时间关系如图3所示。

　　为此，车辆路径惩罚成本函数可表示为：

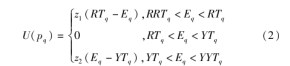
　　式(2)中，z1和z2分别代表在客户期望运输时间窗前、后车辆到达的单位惩罚成本。

　　2.5构建车辆路径模型

　　2.5.1目标函数建立

　　考虑客户等级划分的时间窗车辆路径模型的5个优化目标如下所示。

　　①最低化总运输成本：

　　式(3)中，Dq代表车辆行驶消耗成本，fqw代表决策变量，Cqw代表配送运输所使用车辆，Hq代表车辆固定成本，A代表配送点数量，S代表运输车辆数量。

　　②最大化客户整体潜在价值：

　　③货损成本分析：

　　式(5)中，Lop表示供应点o到配送点p的运输量，r表示货物的市场基准单价，gop表示配送距离，vop表示配送速度。

　　④制冷成本分析：

　　式(6)中，ω表示不同温度条件下运输车辆的能耗率。

　　⑤不同客户等级的惩罚成本分析：

　　式(7)中，h表示常规运输成本。

　　2.5.2构建数学模型

　　因为上述两种局部最优化的优化目标不一定使整体最优。所以，综合考虑上述两种优化目标，可以从整体上把握最优性问题。叠加两种优化目标，获取考虑客户等级划分的时间窗车辆路径模型如下所示：

　　整体目标函数表示为：

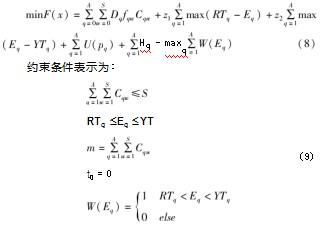
　　3遗传算法求解车辆路径模型

　　3.1遗传算法参数设计

　　非收敛情况不仅发生在简单遗传算法中，而且在单一峰值或单一单调时，这种情况也会发生[11]。为避免这种情况，通常遵循以下的原则设计参数。

　　①初始化种群：通常使用随机费用初始群体。该方法还可以通过近似区间估计法来确定初始种群，并降低算法的开销。最初的种群数量通常是在40-200之间。

　　②变异概率：当变异概率过小使得种群多样性得不到保证时，就会出现某种基因不能遗传给下一代而无法修复的情况。而变异概率过大使得种群多样性得到保证时，会使高阶模式受到破坏。所以变异概率选择0.001~0.2是较为合适的。

　　③交叉概率：通过这一步骤增加新的种群。在使问题的解接近最优解的情况下，用变异算法加快求解速度，求得最优解[12]。在算法的种群性相对离散的情况下，为防止由于变异而使最优解失真，需要选择较小的交叉概率。反之，在算法的种群性相对集中的情况下，为防止早先收敛，需要选择较大的交叉概率。通常可以得到0.4~0.99。

　　④进化代数：迭代次数取决于算法的复杂性程度。随着染色体长度的增长，种群的多样性也逐渐变大，此时的进化代数次数不能过少，否则会导致算法不能收敛而造成早熟线性。进化代数次数的增多会导致时间以及系统资源的浪费。因此，通常取100~3000的进化代数。

　　3.2遗传算法求解过程

　　基于遗传算法的车辆路径模型求解流程如图４所示。

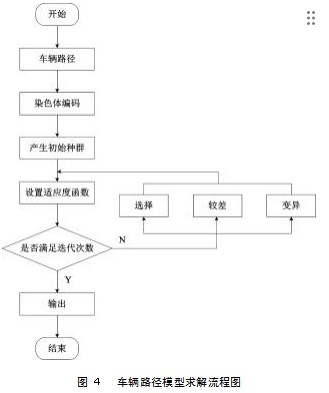
　　根据图４可知具体的求解过程如下：

　　①编码染色体：把车辆路径问题的空间参数转换成染色体，并按照一定的规则，通过基因组合的过程称为编码［１３］。通常的编码需要遵循三个准则：完全性、可靠性以及不重复性。

　　由于配送点数量较多，为提高算法运行效率，利用自然数编码方式，能够直观显示车辆的行驶距离。如果将配送中心用０表示，配送点数量用０，１，…，Ａ表示，运输车辆数量用Ｓ表示，那么编码染色体可表示为ｑ１，ｑ２，…，ｑＡ，ｑＡ＋１，ｑＡ＋２，…ｑＡ＋Ｓ。

　　②产生初始种群：本文模型受限于运输车辆最大载重和里程数，并在此基础上，考虑客户等级划分以及时间窗约束等因素。该算法在初始化种群时，对筛选条件进行设置，使得初始种群满足筛选条件，而不满足筛选条件的初始群体则加快了求解速度。

　　③设置适应度函数：本文以整体目标函数的倒数为适应度函数，以时间窗满意度为初始筛选条件［１４］。如果整体目标函数的倒数过小，不便于观测分析，那么适应度函数可以设为：

　　式（１０）中，λ代表大于整体目标函数的常数。

　　④选择：如果用ｑ表示某客户染色体，用Ｓ表示车辆种群数量，已知适应度函数Ｌｑ，那么选择过程为：首先设置某客户染色体ｑ整体目标函数ｍｉｎＦ（ｘ）的适应度函数Ｌｑ，

　　⑤交叉：在随机群体中，按照一定的交叉概率交换两个不同的个体的某些基因。根据搜索范围的交叉扩大，产生了更多不同的群体［１５］。如果选取第３６８９位置表示为：

　　父代染色体１：１２３４５６７８９父代染色体２：５８９５２５７９０

　　那么子代将这四个位置保留表示为：子代染色体１：∗∗３∗∗６∗８９子代染色体２：∗∗９∗∗５∗９０

　　其中，∗表示需要交叉替换的位置。由于编码的互异性在交叉时是需要注意的，因此子代染色体１的∗位置基因是从父代染色体２中提取的。

　　⑥变异：指的是在群体中改变某些个体的基因。采用先交叉后倒位的实数变异运算方法。

　　⑦终止条件：在预定的条件下停止程序的运行。通常情况下，设定最大迭代数和目标函数的数值都能运行到使目标函数的数值平稳达到预定范围，再选择与最佳染色体相对应的分布路径序列作为最佳解输出。

　　４实验分析

　　为了验证所提算法求解过程的有效性，以某配送中心为１５名客户提供配送服务为例，进行路径规划。配送中心和客户位置分布如图５所示。

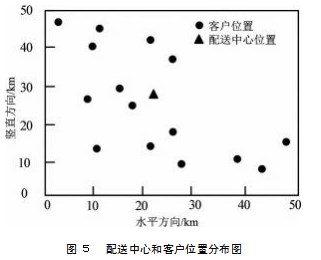
　　设置相关函数为：车辆固定成本Ｈｑ＝１００，客户配送时间敏感性系数δｑ＝０．５，在客户期望运输时间窗前、后车辆到达的单位惩罚成本ｚ１＝１０和ｚ２＝２０，分别采用文献［４］算法、文献［５］算法与所提算法进行车辆路径规划，获取不同算法的车辆满载率对比结果如图６所示。

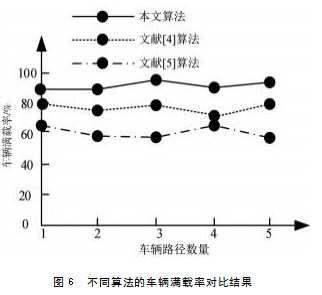
　　分析图6可知，文献[4]算法的平均车辆满载率为79%,文献[5]算法的平均车辆满载率为60%,而所提算法的平均车辆满载率高达91%。由此可知，与文献[4]算法和文献[5]算法相比，所提算法的平均车辆满载率较高。

　　为了进一步验证所提算法的车辆路径求解时间，采用文献[4]算法、文献[5]算法与所提算法，得到不同算法的车辆路径求解时间如图7所示。

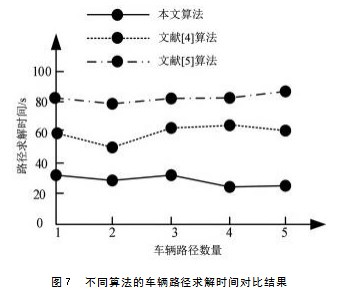
　　分析图7可知，文献[4]算法的平均车辆路径求解时间为59s,文献[5]算法的车辆路径求解时间为82s,而所提算法的平均车辆路径求解时间仅为34s。由此可知，与文献[4]算法和文献[5]算法相比，所提算法的车辆路径求解时间较短。

　　在此基础上，对比文献[4]算法、文献[5]算法和所提算法的车辆配送成本如表1所示。

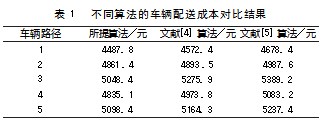
　　根据表1中的数据可知，文献[4]算法的平均车辆配送成本为4976.5元，文献[5]算法的平均车辆配送成本为5075.2元，而所提算法的平均车辆配送成本为4866.2元。由此可知，相比文献[4]算法和文献[5]算法，所提算法能够有效降低车辆配送成本。

　　5结束语

　　本论文设计的考虑客户等级划分的车辆路径遗传算法求解过程充分发挥出了遗传算法的优势，其车辆满载率较高，且求解时间较短、配送成本较低。但该算法在车辆路径规划过程中，未考虑多种车型以及多个配送中心。因此，在下一步的研究中，可以对多种车型和多个配送中心进行构建，并进一步改进车辆路径模型，使求解结果更加精确。

　　［参考文献］

　　[1]Wang X Y,Wasil E.On the road to better routes:Five decades of published research on the vehicle routing problem[J].Networks,2021,77(1):66-88.

　　[2]Elham M,Ryan L,Shiv M,Luke G.A decision support system for grain harvesting,storage,and distribution logistics[J].Knowledge-Based Systems,2021,223:107-117.

　　[3]Liu P D,Li Y.Multiattribute decision method for comprehensive logistics distribution center location selection based on 2-dimensional linguistic information[J].Inform-ation Sciences,2020,538:209-244.

　　[4]Feng L,Huang Y,Tsang I W,Gupta A,Ong Y S.Towards Faster Vehicle Routing by Transferring Knowledge From Customer Representation[J].IEEE Transactions on Intelligent ransportation Systems,2020(9):1-14.

　　[5]Yan X,Huang H,Hao Z,Wang J.A Graph-Based Fuzzy Evolutionary Algorithm for Solving Two-Echelon Vehicle Routing Problems[J].IEEE Transactions on Evolutionary Computation,2020,24(1):129-141.

　　[6]Tanoumand N,Ünlüyurt T.An exact algorithm for the resource constrained home health care vehicle routing problem[J].Annals of Operations Research,2021(1):1-29.

　　[7]Luo Z,Lim A,Qin H,Zhu W.Branch and price and cut for split-delivery vehicle routing problem with time windows and linear weight-related cost[J].Operations Research,2019,59(1-2):75-77.

　　[8]郭保青，郝树运，朱力强，余祖俊．基于改进蚁群算法的多AGV泊车路径规划[J].交通运输系统工程与信息，2018,18(06):55-62+80.

　　[9]王雨，谢峰，刘玉磊，朱翔．基于改进势场蚁群算法的自动引导小车路径规划研究[J].制造业自动化，2019,41(07):70-74.

　　[10]王秀芬．窄通道路径规划的改进人工势场蚁群算法[J].计算机工程与应用，2019,55(03):104-107+125.

　　[11]Wang H J,Fu Z J,Zhou J J,Fu M Y,Ruan L.Cooperative collision avoidance for unmanned surface vehicles based on improved genetic algorithm[J].Ocean Engineering,2021,222(4):108612.

　　[12]Wang K,Gong Y,Peng Y L,Hu C L,Chen N C.An improved fusion crossover genetic algorithm for a time-weighted maximal covering location problem for sensor siting under satellite-borne monitoring[J].Computers&geosciences,2020,136(3):1-13.

　　[13]Ghannami A,Li J,Hawbani A,Alhusaini N.Diversity metrics for direct-coded variable-length chromosome shortest path problem evolutionary algorithms[J].Computing,2020,103(6):313-332.

　　[14]梁世娇，柴争义．基于多目标自适应Memetic算法的复杂网络社区检测[J].江苏大学学报（自然科学版），2020,41(03):262-267+280.

　　[15]Zhang Q B,Yang S X,Liu Min,Liu J X,Jiang L.A new crossover mechanism for genetic algorithms for steiner tree optimization.IEEE Transactions on Cybernetics,2020(1):1-12.