【摘要】加工和维护时长的波动使生产实际运行与计划之间产生较大偏离，使所预留的维护契机变得不可行。为此，引入两个不确定参数描述加工和维护时长的波动程度和约束条件的允许违背程度，将考虑预防维护的多工艺路线柔性作业车间鲁棒调度问题转换为确定条件下的鲁棒对等问题；基于编码方式和邻域搜索算法设计了一种模拟退火算法求解该问题，将鲁棒调度方案与企业实际生产方案进行对比，通过实验证明了鲁棒优化方案的有效性。

　　【关键词】多工艺路线；柔性作业车间；随机工时；随机维护时间

　　在生产计划编制时，需考虑源于设备、工艺等方面不确定因素的影响。从设备角度而言，随着设备服役时长增加，性能逐渐劣化，需进行预防性维护，提高设备在使用周期内的可靠性和可用性，避免因设备故障造成非计划性生产中断和经济损失。在生产计划编制时，将预防维护集成到生产计划编制过程中，以较少的生产效率损失为代价，获取更合适的设备维护契机。从工艺等角度而言，生产中的多工艺路线可选问题进一步提高了调度的复杂性，且随着设备性能或操作人员状态异动，操作工时频繁波动，生产实际运行与计划之间产生较大偏差，提前预留的维护契机可能从最合适变成了不可行。故需研究考虑预防维护的多工艺路线柔性作业车间鲁棒调度，既提升生产计划的鲁棒性，又确保所留预防维护时机的较优性。

　　针对预防维护与生产计划的集成优化，蒋凯丽等[1]、Zhang等[2]、An等[3]、Golmakani等[4]有较突出的研究，他们将设备预防维护的起止时间转化为决策变量，综合机器分配、生产排序及操作定时等变量，进行联合决策。针对多工艺路线柔性作业车间调度问题，李聪波等[5]针对面向能耗的多工艺路线柔性作业车间分批调度问题，以车间总能耗最低和最小化最大完工时间为目标建立数学模型。杨小龙等[6]为解决多工艺路线柔性作业车间调度问题，提出一种递阶结构的三阶段蚁群算法，分别进行工艺路线选择、工序的机器选择、工序排序，并通过实验证明该算法性能的优越性。杨洪涛等[7]针对多工艺路线下柔性作业车间工艺与布局的联合优化问题，以总物流成本最低为目标，建立了多工艺路线和车间布局联合优化模型，并提出了一种多决策变量优化算法进行求解，通过实例验证了该优化方法的有效性。李言等[8]针对多目标工艺规划与调度集成问题，以最大完工时间和最大负载为目标建立模型，设计一种非支配排序遗传算法进行求解，通过实验证明了模型的正确性和算法的有效性。

　　然而，上述文献中，考虑预防维护车间调度的研究并未集成多工艺路线问题，而在多工艺路线调度问题的研究中并未集成预防维护，同时，两种问题下的加工时长和机器的维护时长为定值。而在实际生产中，维护活动持续时长和加工时长是变化的，其变动服从一定概率分布［９］。综合考虑多工艺路线及预防维护将其集成到生产计划中的思路是可行的，但其鲁棒性不强、对随机扰动的抗干扰能力较差。故需将加工时长和机器的维护时长变动融入调度方案，以提升其鲁棒性。

　　１问题描述与模型建立

　　１．１问题描述

　　不确定工时和预防维护时间下的多工艺路线柔性作业车间调度问题，可以描述为：ｎ个待加工工件ｉ（ｉ＝１，２，３…ｎ），在ｍ台机器上进行加工；每个工件的可选工艺路径集合为Ｌｉ，不同工艺路线下均含多道工序且其数量不尽相同。在各工艺路线下，每个工件的工序顺序已知，且每道工序可在多台不同机器上进行加工；每台机器的预防维护周期、维护时长及加工各工序的时长均不相同；其中，各机器的维护时长和工序的加工时长是在一定范围内变动的，且服从某种概率分布。该问题的求解，即为每个工件选择合适的工艺路线，且在该工艺路线下通过将每道工序分配给适当的机器，确定每台机器上各工序的执行顺序；根据各机器的预防维护周期，确定各自的预防性维护位置，促使车间生产在一定程度上不受随机波动因素的影响，且使某些指标达到最优，如最小化最大完工时间等。预防性维护周期一般根据可用性角度确定，假定机器失效函

　　数ｆ(τ)＝∫λ(ｔ)ｄｔ＝（τ／θ）β，预防维护时长为ｔｋ，则在预防维护周期内机器可用性为Ａ（τ）＝τ／（τ＋ｆ(τ)ｔｒ＋ｔｋ），当机器可用性最大化时，最佳预防维护周期为

　　１．２模型建立

　　１．２．１假设条件

　　针对该问题做以下假设：①各工件的可选工艺路线优先级相同；②每个工件一次只能选择一条工艺路线；③所有工件在零时刻均可被加工；④各工件的工序顺序已知；⑤每台机器一次只能加工一道工序；⑥每个工件的每道工序都只能分给一台机器加工，且各工序一旦开始就不能中断；⑦每个工件的每道工序都有多台可选加工机器，且在每个可选机器上的加工时间已知，但实际加工时间为给定变动范围内的随机变量；⑧各机器上相邻两个加工工件之间无需切换时间；⑨各机器上的预防维护周期和维护时间已知，实际维护时间为给定变动范围内的随机变量；OI0各机器进行预防维护后，其性能恢复如新。为便于描述引入以下符号。

　　１．２．２鲁棒对等模型建立

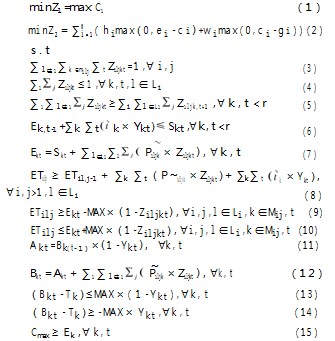
　　式（１）（２）表示目标函数是最大完工时间和最大交货惩罚周期的最小值。式（３）保证每个工件只能选择一条工艺路线并且各工序在加工时只能分配给一台机器；式（４）表示一台机器在工作时不能再加工其他工序；式（５）表示各机器上的工序有序安排；式（６）表示各个机器在前一事件点完成后才能开始下一个；式（７）表示任务一旦开始不允许中断；式（８）表示各个工件在其前一工序完成后才能开始下一道工序；式（９）和（１０）建立各工序完成时间与各事件点完成时间的一一对应关系；式（１１）表示机器在进行预防维护之后，其性能恢复如新；式（１２）表示机器的加工寿命与加工时间的对应关系；式（１３）和（１４）用来表示是否进行预防维护的判断条件。式（１５）是完工时间约束。

　　观察模型，在式（６）（７）（８）（１２）中存在随机变量ｋ和Ｐ~ｉｌｊｋ。引入两个不确定参数，加工时间和维护时间波动程度ε以及约束条件的允许违背程度ｋ，其中，ε（ε＞０）为给定的波动水平，可调整和控制不确定参数的波动幅度。ε越大，不确定参数的波动程度越大，调度方案吸收随机扰动所需的亢余越大，其性能损失越大。不确定参数ｋ描述约束条件允许违背的程度，用来实现调度方案和约束条件允许违背的折中，则１－ｋ表示不等式成立的概率，此时求出的解成为约束条件允许违背程度为ｋ的鲁棒解［１１］。假定工件的加工时间和维护时间的扰动量δ均服从参数为１的指数分布，其分布函数和分位点如下：

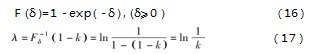
　　用分位点代替随机波动部分，可将式（６）（７）（８）（１２）的不确定部分转换为对等的确定性的问题。

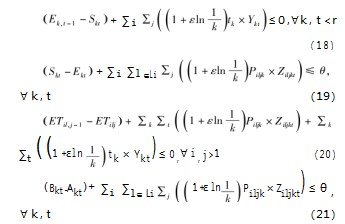
　　结合式（１６）（１７）（１８）（１９）可得到，加工时间和维护时间服从参数为１的指数分布的鲁棒对等模型。

　　２算法设计

　　２．１编码

　　采用基于工艺路线、工序和机器的三层编码方式，每个解由三部分构成。在整个粒子中，工艺路线部分中的长度表示工件数，数字部分表示该位置工件选择的工艺路线号码；工序部分中的数字表示工件号，出现的次数表示该工件号所选工艺路线下的工序数；机器码部分各位置的数字表示与之对应的工序码位置工序所选机器号码。如图１所示：工艺路线码中的第一个位置的数字１，表示第一个工件选择１号工艺路线进行加工；工序码中的第一个位置的数字１，表示第一个工件的第一条工艺路线的第一道工序，第四个位置的数字１表示第一个工件的第一条工艺路线的第二道工序；机器码部分的第一个数字１，表示将第一个工件的第一道工序分配给一号机器进行加工。

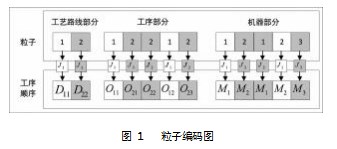
　　２．２解码

　　解码就是编码的反向操作，在考虑预防维护的多工艺路线柔性作业车间鲁棒调度问题中，需要关注五个问题：第一，为各工件选择工艺路线；第二，确定工件在选择的工艺路线下各工序的加工机器；第三，确定当前工序在选定机器上的开始和完成时间；第四，根据各机器的维护周期确定其预防维护的开始和结束时间；第五，对在插入预防维护后产生的非法解进行处理；根据编码规则，在已生成的解中，工艺路线部分和机器选择部分已经对上述前两个问题进行确定，故解码主要关注后三个问题。

　　①确定当前工序在所选机器上的开始和结束时间。

　　首先，对该机器上的所有空闲时间进行判断，看其是否可以插入当前工序Ｏｉｌｊ进行加工；若是，则将该工序插入相应的空闲时间段进行加工，同时更新该机器的加工序列，否则，将该工序放置于机器的末尾进行加工，同时更新该工序的开始和结束时间。

　　满足式（２２）才能插入机器的空闲时间[Ｔａ，Ｔｂ]进行加工

　　若满足条件，在机器空闲时间插入工序进行加工的条件，则工序Ｏｉｌｊ的开始加工时间为：

　　②确定各机器的预防维护时间。

　　根据各机器上各事件点已安排的加工工件序列，按照式（１９）计算该机器的寿命，并判断机器寿命与维护周期的关系，进而插入预防性维护活动。

　　当机器寿命等于维护周期：

　　在计算机器寿命时，当在事件点ｔ的工序加工后，机器寿命等于预防维护周期，则在该事件点之后进行预防性维护，

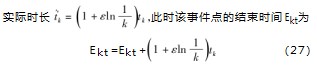
       其当机器寿命大于维护周期：

　　在计算机器寿命时，当在事件点t的工序加工后，机器寿命大于预防维护周期，则在该事件点的前一事件点结束后进行预防性维护，

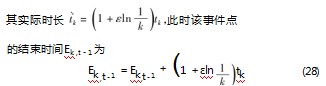
　　③对各机器上已安排工序中的非法解进行处理。

　　在进行预防维护后，各机器上的各事件点之间的开始和结束时间可能会违背数学模型中的约束(6),对此种情况采取右移的操作进行处理。在此操作完成后，各工件工序的开始和结束时间可能会违背数学模型中的约束(8),对该情况同样采取右移操作，以保证解的可行性。

　　2.3适应度值计算

　　在模拟退火算法中，用适应度值来评价一个解的优劣，以及是否接受其为新解。在本章不确定工时和维护时间下多工艺路线柔性作业车间调度模型中，有最小化最大完工时间和最小化交期惩罚两个目标函数，通过引入两个权重系数α、β,将多目标问题转换为单目标进行求解，故适应度计算如式(29),其值fitness(x)越小，结果越优。

　　fitness(x)=min(αZ1+βZ2)(29)

　　2.4基于邻域的搜索机制

　　在模拟退火算法中，新解是通过对旧解施加扰动产生的，即对当前解通过扰动后产生一个位于解空间的解[12]。在标准模拟退火算法中，通常为减少算法耗时，其扰动过程均设置得较为简单，如：置换、逆序等，扰动方法的选择决定新解的邻域结构，而针对不同问题需选取合适的扰动过程。但标准模拟退火算法通常只通过产生一种领近解进行搜索，这降低了算法的搜索效率。为此，本文结合邻域搜索算法，根据工艺路线码、工序码、机器码三层编码的方式，分别从工艺路线码是否进行扰动两个方面生成三种邻域，并对三种邻域下的新解及旧解进行择优操作。

　　①工艺路线码部分发生改变。

　　首先，针对工艺路线码部分，随机选取两个工件，分别从这两个工件的可选工艺路线集中选取一个替换已选中的工艺路线；其次，根据替换后的工艺路线码，对工序码和机器码进行修正操作，即将选取的两个工件的工序码和机器码替换成新工艺路线下对应的工序码和机器码。其过程如图2所示。

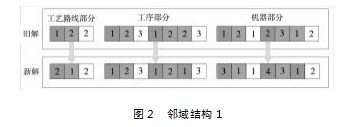
　　②工艺路线码部分发生改变。

　　首先，针对工艺路线码部分，随机选取两个工件，分别从这两个工件的可选工艺路线集中选取一个替换已选中的工艺路线；根据替换后的工艺路线码，对工序码和机器码进行修正操作，即将选取的两个工件的工序码和机器码替换成新工艺路线下对应的工序码和机器码。对修正后的工序码和机器码采取逆序的方式生成新的领近解：在工序码中随机选取两个距离大于2的位置，将两个位置中间的工序码进行逆序处理，对机器码部分相同位置的机器码也做同样的处理。其过程如图3所示。

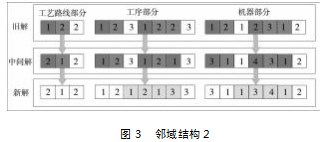
　　③工艺路线码部分不变。

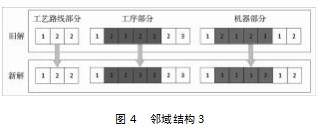
　　此时工艺路线码部分不做处理，由于机器码各位置的机器号对应工序码该位置工序所选加工机器，故对工序码和机器码采取前插的方式生成新的领近解。即在工序码和机器码中随机选取相同的两个距离大于2的位置，将两个位置间的基因的最后一个基因插入第一个基因位之前，其余的基因依次向后移动一个位置形成邻域。其过程如图4所示。

　　2.5内循环机制

　　传统的SA算法，在同一温度值T下需执行多次Metropolis算法以保证全局搜索能力，但不够灵活，因为内循环次数过多会增加算法运行时间，次数过少则损失解的质量。为此，引入计数器R,用以记录内循环过程中局部解未被提高的次数。在每次内循环开始，便设置R=0,然后每执行一次内循环，便判断局部解是否被提高，若是则令R=0,否则R+=1。当R大于给定的上限时，则跳出当前温度的内循环。

　　2.6解的接受准则

　　模拟退火算法以较高初始温度出发，伴随温度参数的不断下降结合一定的概率突跳特性，在解空间中随机寻找目标函数的全局最优解，即局部最优解能概率性地跳出并最终趋于全局最优。具体过程如下：将当前解算出适应度值FO与相邻解Fi进行比较，若相邻解优于当前解则用相邻解替换当前解，否则以一定概率接受领近解。本文采用标准SA算法的Metropolis准则，其过程如式(30)所示。

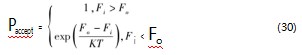
　　3实例仿真分析

　　3.1实例数据

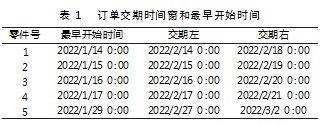
　　本文所采用的案例来自某电机厂转轴加工车间部分数据（取其中5个工件），各工件的交期信息如表1所示。各工件的工艺路线及各工艺路线下各工序的可选机器和加工时间如表2所示。其中，工序可选机器列中每列表示一道工序，数据表示该工序的可选机器集，为空则表示对应工件工艺路线下没有该工序；加工时间列对应各工序在可选机器上的加工时间。如：工件1的一号工艺路线有四道工序，第一道工序的可选机器号为(1,2,3),其对应的加工时间分别为(340,340,340)。

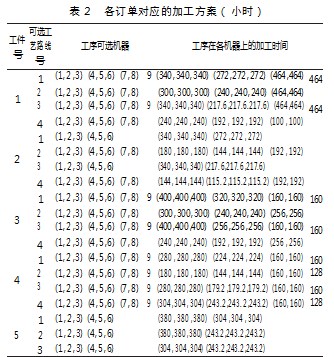
　　3.2实例验证

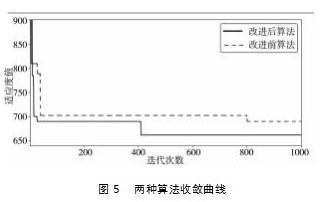
　　本文仿真实验的硬件环境为Intel(R)Core(TM)i7-10710U CPU 1.10GHz,RAM16G,软件环境为Windows10家庭中文版，采用Python3.7编写算法。算法各参数设置如下：初始温度T=10,温度下限为T0=1,每个温度内迭代次数L=100,局部解未被更新最大次数R=50。将本文改进模拟退火算法与原始算法进行对比，其收敛曲线如图5所示。改进前模拟退火算法在迭代800多次后的得到最优解697.8,而改进后算法在迭代400多次得到最优解660.6。改进后算法以较少的次数收敛到最优解，让解向着可行的方向进化和快速收敛，相较于改进前模拟退火有更好的收敛速度，同时可以搜索到更好的解，该近似算法具有良好的性能。

　　在某军工电子产品精密加工实际生产执行过程中，其生产计划以人工的方式进行制定，为应对随机扰动带来的调度方案与执行的偏差，通常采用固定系数对标准加工时间进行放大处理，其放大系数为1.3。为进一步分析本文鲁棒优化方法的有效性，将本节中的5个工件的人工加工调度方案与优化后的结果进行比较，表3为人工加工调度方案，表4为优化后调度方案。

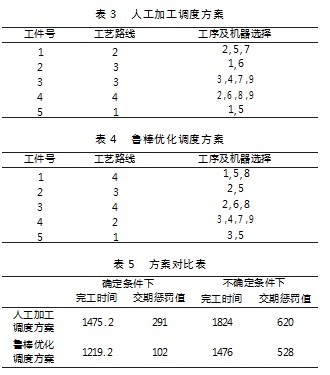
　　分析表5可知，在确定条件下，经算法优化后的方案所求得的完工时间和交期惩罚值比实际调度方案更小，说明本文改进算法具有良好的性能。鲁棒优化调度方案在不确定条件下求得解的完工时间与确定条件下差值为256.8,而实际调度方案的这一值为348,说明本文对随机工时和维护时间两个不确定参数的鲁棒优化策略，比实际的固定放大系数据有更好的效果。综上所述，本文的鲁棒优化策略是有效的。

　　4总结

　　针对随机工时和维护时间下多工艺路线下的柔性作业车间调度问题，采用周期性维护策略，建立了加工时长和预防维护时长服从指数分布的鲁棒对等问题模型，基于模拟退火算法，根据问题特点设计三层编码方式进行编码，并据此设计三种邻域结构，用以产生领近解并和旧解进行择优操作，通过设置局部解未更新的迭代次数上限，跳出该温度的循环进入下一温度进行搜索，从而提高算法收敛速度。通过将本文鲁棒优化方法得到的调度方案，与企业实际生产调度方案进行对比，表明本文的鲁棒优化策略是有效的并且改进模拟退火算法具有良好的性能。

　　［参考文献］

　　[1]蒋凯丽，陆志强，崔维伟．考虑周期预防性维护的两阶段混合流水线调度[J].计算机集成制造系统，2017,23(3):616-623.

　　[2]Zhang Zikai,Tang Qiuhua.Integrating preventive maintenance to two-stage assembly flow shop sche-duling:MILP model,Services and Manufacturing Journal,2022,34(1):156-203.

　　[3]An Youjun,Chen Xiaohui,Hu Jiawen,et al.Joint optimization of preventive maintenance and production rescheduling with new machine insertion and processing speed selection[J].Reliability Engineering&System Safety,2022,220:108269.
       [4]Hamid Reza Golmakani,Ali Namazi I.Multiple-route jobshop scheduling with fixed periodic and age dependent preventive maintenance to minimize makespan[J].Journal of Quality in Maintenance Engineering,2012,18(1):60-78.

　　[5]李聪波，沈欢，李玲玲，等．面向能耗的多工艺路线柔性作业车间分批优化调度模型[J].机械工程学报，2017,53(5):12-23.

　　[6]杨小龙，张洁，等．基于三阶段改进蚁群算法的多工艺路线柔性作业车间调度[J].制造业自动化，2015(8):51-55.

　　[7]汤洪涛，梁佳炯，陈青丰，等．柔性车间的多工艺路线与布局联合优化[J].计算机集成制造系统，2022,28(2):495-506.

　　[8]李言，巴黎，曹源，等．考虑多目标的工艺规划与调度集成问题研究[J].中国机械工程，2015(17):2344-2351+2373.

　　[9]Javad Seif,Mohammad Dehghanimohammadabadi,Andrew Junfan Yu.Integrated preventive maintenance and flow shop scheduling under uncertainty[J].Flexible Services and Manufacturing Journal,2019,32:852-887.

　　[10]周炳海，蒋舒宇，王世进，等．集成生产与预防性维护的流水线车间调度算法[J].大连海事大学学报，2007,33(3):32-35.

　　[11]唐秋华，何明，何晓霞，等．随机工时下柔性加工车间的鲁棒优化调度方法[J].计算机集成制造系统，2015,21(4):1002-1012.

　　[12]陈科胜，鲜思东，郭鹏．求解旅行商问题的自适应升温模拟退火算法[J].控制理论与应用，2021,38(2):245-254.