摘要:用空间向量研究距离问题是新教材的新增内容,本文精选了一些往年的优秀高考题,阐述向量法在解决空间距离问题中的应用.

　　关键词:高考;空间距离;向量;解法

　　空间距离是立体几何的重要内容,是高考热点,也是教学难点,它包括两点间的距离、点到直线的距离、点到平面的距离、平行线间的距离、异面直线间的距离、直线到平面的距离、平行平面间的距离等.

　　1两点间的距离设P1(x1,y1,z1),P2(x2,y2,z2)是空间中任意两点,则P1 P2=(x2-x1)2+(y2-y1)2+(z2-z1)2→=|P1 P2|.即空间任意两点间的距离等于从其中一点指向另一点的向量的长度.

　　例1(2013年北京卷文8)如图1,在正方体ABCD-A1 B1 C1 D1中,点P为对角线BD1的三等分点,点P到各顶点的距离的不同取值有().A.3个B.4个C.5个D.6个

　　分析建立如图2所示的空间直角坐标系,设正方体的棱长为3,可得各顶点的坐标,求出点P的坐标,再利用两点间的距离公式即可得出结论.

　　解析以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图2所示的空间直角坐标系,不妨设正方体的棱长为3,则A(3,0,0),B(3,3,0),C(0,3,0),D(0,0,0),A1(3,0,3),B1(3,3,3),C1(0,3,3),D1(0,0,3).从而DB=(3,3,0),BD1=(-3,-3,3).

　　因为=B=(-1,-1,1),

　　所以=+=(2,2,1).

　　所以P(2,2,1).

　　所以PA=PC=PB1=12+22+12=6,

　　PD=PA1=PC1=22+22+12=3,

　　PB=3

　　PD1=22+22+22=2 3.

　　故点P到各顶点的距离的不同取值有6,3,3,2 3共4个,故选B.

　　点评本题主要考查空间中两点间的距离的求法,体现了数学运算和直观想象等核心素养.选择适当的位置建立空间直角坐标系并求出点P的坐标是解题的关键,属于中档题.变式1(2002年全国卷理18)如图3,正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<2).(1)求MN的长.

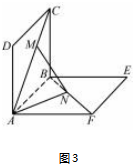
　　(2)当a为何值时,MN的长最小?

　　2点到直线的距离

　　如图4,直线l的方向向量为u,A是直线l上的定点,P是直线l外一点,则点P到直线l的距离d=||2-(·uö2.

　　即直线外一点到直线的距离等于从直线上某定点指向该点的向量与其在直线上的投影向量的平方差的算术平方根.

　　求点到直线的距离的一般步骤是:

　　(1)选择适当的位置建立空间直角坐标系;

　　(2)求直线上某定点指向该点的向量和直线的方向向量;

　　(3)代入公式计算.

　　平行线间的距离可转化为点到直线的距离.例2(2010年全国Ⅱ卷理11)与正方体ABCD-A1 B1 C1 D1的三条棱AB,CC1,A1 D1所在直线的距离相等的点().

　　解析点D,B1显然满足条件,下面证明直线DB1上的点都满足条件.

　　以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图5所示的空间直角坐标系,设正方体的棱长为1,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1)C1(0,1,1),D1(0,0,1).从而=(0,1,0),=(-1,0,→0),DB1=(1,1,1).

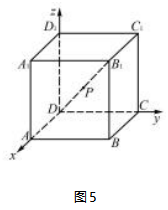
　　设P为直线DB1上的任意一点,且=λD,则=(λ,λ,λ).所以=+=(λ-1,λ,λ).

　　点P到AB的距离d1=||2-(ö2=(λ-1)2+λ2.

　　同理可得点P到CC1的距离2=|2-(·ö2èCC1ø=(λ-1)2+λ2,点P到D1A1的距离3=D1A1ø=(λ-1)2+λ2.

　　所以d1=d2=d3,故选D.

　　点评本题主要考查空间中点到直线的距离的求法,体现了数学运算和直观想象等核心素养.解题关键是选择适当的位置建立空间直角坐标系,正确运用点到直线的距离公式,属于中档题.变式2(2009年湖南卷理7)正方体ABCD-A1 B1 C1 D1的棱上到异面直线AB,CC1的距离相等的点的个数为().A.2 B.3 C.4 D.5

　　3点到平面的距离

　　如图6,已知平面α的法向量为n,A是平面α内的定点,P是平面α外一点,则点P到平面α的距离d=.

　　即平面外一点到平面的距离等于从平面内某定点指向该点的向量在平面法向量方向的投影向量的长度.求点到平面的距离的一般步骤是:

　　(1)选择适当的位置建立空间直角坐标系;

　　(2)求平面内某定点指向该点的向量和平面的法向量;

　　(3)代入公式计算.

　　直线到平面的距离、两平行平面间的距离均可转化为点到平面的距离.

　　例3(2019年上海卷17)在长方体ABCD-A1 B1 C1 D1中,M为BB1上一点,已知BM=2,CD=3,AD=4,AA1=5,求点A到平面A1 MC的距离.

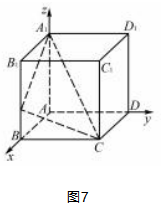
　　分析建立如图7所示的空间直角坐标系,求出向量和平面A1 MC的法向量n,代入公式计算即可.

　　解析以A为原点,AB,AD,AA1所在直线分别为x轴、y轴、z轴,建立如图7所示的空间直角坐标系,则A(0,0,0),C(3,4,0),A1(0,0,5),M(3,0,2).从而=(-3,0,-2),M=(-3,0,3),=(0,4,-2).设平面A1 MC的法向量为n=(x,y,z),则n⊥MC,且n⊥MA1.所以{解得íz.取z=2,得n=(2,1,2).所以点A到平面A1 MC的距离→d=|MA·n||-3×2+0×1+(-2)×2|=22+12+22=.

　　点评本题主要考查点到平面的距离的求法,体现了数学运算和直观想象等核心素养.解题关键是正确求出平面的法向量,准确运用点到平面的距离公式,属于中档题.

　　例4(2008年福建卷理18)如图8,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=2,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.

　　(1)求证:PO⊥平面ABCD;

　　(2)线段AD上是否存在点Q,使得它到平面

　　PCD的距离为?若存在,求出的值;若不存在,请说明理由.分析(1)先证PO⊥AD,再利用面面垂直的性质定理,就能证明PO⊥平面ABCD.

　　(2)先证OC,OD,OP共点且两两垂直,建立如图9所示的空间直角坐标系,再假设线段AD上存在符合题意的点Q(0,y,0)(-1≤y≤1),求出平面PCD的法向量n和,根据点Q到平面PCD的距离为3列方程求解.

　　解析(1)在△PAD中,因为PA=PD,O为AD的中点,所以PO⊥AD.又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,PO⊂平面PAD,所以PO⊥平面ABCD.

　　(2)假设线段AD上存在点Q,使得它到平面

　　PCD的距离为.因为底面ABCD为直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC=2,所以OC⊥AD.又由(1)知OC,OD,OP共点且两两垂直.以O为原点,OC,OD,OP所在直线分别为x轴、y轴、z轴建立如图9所示的空间直角坐标系,则C(1,0,0),D(0,1,0),P(0,0,1).从而=(-1,0,1),=(-1,1,0).设平面PCD的法向量为n=(x,y,z),则n⊥,且n⊥.所以{解得x=y=z.取x=1,得n=(1,1,1).设Q(0,y,0)(-1≤y≤1),则=(-1,y,0).由|·n|=|-1+y|=3解得y=-,或y=(舍去).所以线段AD上存在点Q满足题意,此时AQ 1=QD 

　　点评本题主要考查直线与平面垂直的证明,考查与空间距离有关的探索性问题的解法等,体现了数学建模、逻辑推理、数学运算和直观想象等核心素养.解题关键是选择适当的位置建立空间直角坐标系,建立方程模型进行求解,属于中档题.

　　变式3(2013年上海卷理19)在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.

　　四、异面直线间的距离

　　如图10,若CD是异面直线a,b的公垂线(与a,b都垂直且相交),A,B分别为a,b上的定点,设向量n⊥,n⊥,则n//.故异面直线a,b间的距离d=|CD|=→|AB·n|n.

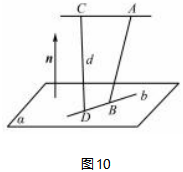
　　即异面直线间的距离等于从其中一条直线上的某定点指向另一条直线上的某定点的向量在公垂线上的投影向量的长度.

　　求异面直线间的距离的一般步骤是:

　　(1)选择适当的位置建立空间直角坐标系;

　　(2)求一条直线上的某定点指向另一条直线上的某定点的向量和公垂线的方向向量;

　　(3)代入公式计算.

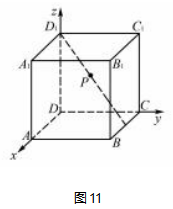
　　例5(2013年北京卷理14)在棱长为2的正方体ABCD-A1 B1 C1 D1中,E为BC的中点,点P在线段D1 E上,点P到直线CC1的距离的最小值为.

　　分析点P到直线CC1的距离的最小值就是异面直线D1 E与CC1间的距离.解析以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图11所示的空间直角坐标系,则D1(0,0,2),E(1,2,0),C(0,2,0),C1(0,设n=(x,y,z)是异面直线D1 E与CC1公垂线→→

　　所以1îz=0.取x=2,则y=-1,所以n=(2,-1,0).故点P到直线CC1的距离的最小值→dmin=|EC·n|=|-1×2+0×(-1)+0×0|=2 522+(-1)2+02 5.

　　点评本题主要考查异面直线间的距离的求法,体现了数学运算和直观想象等核心素养.解题关键是把求点P到直线CC1的距离的最小值问题转化为异面直线D1 E与CC1间的距离问题,属于中档题.

　　变式4(1989年全国卷理18)已知圆柱的底面半径是3,高是4,A,B两点分别在两底面的圆周上,并且AB=5,那么直线AB与轴OO′之间的距离等于.

　　参考文献:

　　[1]安全.空间距离问题求解方法赏析[J].高中数学教与学,2017(08):48-49.