摘要:本文从设点坐标、参数几何意义和极坐标应用三种不同角度对极坐标与参数方程问题做了“破题”分析和反馈练习.

　　关键词:极坐标;参数方程;几何意义

　　极坐标与参数方程作为选做题,由于难度不大,极易被考生选择.文章从设点坐标、参数几何意义和极坐标应用三种不同方法入手,对极坐标与参数方程问题做了例题总结,在例题总结中强化基本概念和几何意义,找到“破题”入口.1利用参数方程的参数几何意义几个常见的参数方程:

　　(1)圆(x-a)2+(x-b)2=r2的参数方程(α为参数),参数α的几何意义是OP与x轴正方向的夹角.P是圆周上任意一点.

　　(2)过定点M0(x0,y0),倾斜角为α的直线参数方程(t为参数),参数t的几何意义是直线上有向线段M0 M的数量,即M0 M=t(其中M(x,y)是直线上任意一点),当点M在M0上方时,t>0;当点M与M0重合时,t=0;当点M在M0下方时,t<0.已知P1,P2两点都在直线上,对应的参数分别为t1和t2,则P1 P2|=|t1 t2|.P1 P2中点对应的t值为t=(t1+t2).

　　(3)椭圆+=1(a>b>0)的参数方程为参数),参数φ的几何意义是椭圆上任意一点M所对应的圆的半径OA(或OB)的旋转角(称为点M的离心率角)(φ∈[0,2π)).

　　(4)双曲线-=1(a>0,b>0)的参数方程(φ为参数),参数φ的几何意义点M所对应的圆的半径OA的旋转角(称为点M的离心角).

　　(5)抛物线y2=2px(p>0)的参数方程为参数),参数t的几何意义表示抛物线

　　上除顶点外的任意一点与原点连线的斜率的倒数.

　　例1(2018年Ⅱ卷)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为为参数).

　　(1)求C和l的直角坐标方程;

　　(2)若曲线C截直线l所得线段的中点坐标为(1,2),求l的斜率.

　　解析(1)C的直角坐标方程:+=1.

　　当cosα≠0时,l的直角坐标方程为

　　y=xtanα+2-tanα;

　　当cosα=0时,l的直角坐标方程为x=1.

　　(2)将l的参数方程代入C的直角坐标方程得(1+3cos2α)t2+4(2cosα+sinα)t-8=0.①因为曲线C截直线l所得线段的中点(1,2)在

　　C内,所以①有两个解,设为t1,t2,则t1+t2=4(2cosα+sinα)1+3cos2α于是直线l的斜率k=tanα=-2.

　　“破题”与评注关键是恰巧线段中点在椭圆内部,利用直线的参数几何意义,求出直线斜率.本题考查曲线的极坐标、参数方程与普通方程之间的转化,考查直线参数方程的几何意义,对于这一类问题的处理,一般就是将直线的参数方程与曲线普通方程联立,借助韦达定理求解问题.

　　反馈练习(2021年蚌埠第三中学高三模考)坐标系与参数方程:在平面直角坐标系中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为(2,),直线l的极坐标方程为ρcos(θ-)=a,且点A在直线l上.

　　(1)求a的值和直线l的直角坐标方程及l的参数方程;

　　(2)已知曲线C的参数方程为为参数),直线l与C交于M,N两点,求+的值.

　　解析(1)因为点A∈l,所以a=2.

　　由ρcos(θ-)=a,得(ρcosθ+ρsinθ)=2.

　　于是l的直角坐标方程为l:x+y-2=0;(2)由C:得(x-4)2+(y-3)2=25.将l的参数方程代入(x-4)2+(y-3)2=25,得t2+2 t-12=0.

　　设该方程的两根为t1,t2,由直线l的参数t的几何意义及曲线C知,|AM|·|AN|=|t1|·|t2|=|t1 t2|=12,|AM|+|AN|=|t1|+|t2|=|t1-t2|=

　　(t1+t2)2-4t1 t2=5 2+

　　“破题”与评注关键是利用直线参数方程参数的几何意义得出|AM|·|AN|=|t1|·|t2|=|t1 t2|,|AM|+|AN|=|t1|+|t2|=|t1-t2|.本题考查曲线的极坐标、参数方程与普通方程之间的转化,考查直线参数方程的几何意义,将直线的参数方程与普通方程联立,借助韦达定理求解,属于常规题.

　　2利用参数方程设点坐标

　　例2(2017年Ⅰ卷)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为为参数).

　　(1)若a=-1,求C与l的交点坐标;

　　(2)若C上的点到l的距离的最大值为,求a.解析(1)曲线C的普通方程为+y2=1.当a=-1时,直线l的普通方程为x+4y-3=0与C联立解得交点坐标为(3,0),(-,).

　　(2)直线l的普通方程为x+4y-a-4=0,故C上的点(3cosθ,sinθ)到l的距离为d=

　　|3cosθ+4sinθ-a-4|

　　17.

　　当a≥-4时,dmax=a+9=,所以a=8;综上,a=8或a=-16.

　　“破题”与评注先把直线与椭圆的参数方程化为直角坐标方程,联立两个方程,可得交点坐标,利用椭圆的参数方程,求椭圆上一点到一条直线的距离的最大值,可以直接利用点到直线的距离公式,表示出椭圆上的点到直线的距离,此时设出点的坐标是关键,即利用三角换元法将问题转化为三角函数的最值求解问题,利用三角有界性求出最值,进而求得参数a的值.反馈练习(2016年全国卷理)在直角坐标系xOy中,曲线C1的参数方程为(α为参数),以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+)=2 2.

　　(1)写出C1的普通方程和C2的直角坐标方程;

　　(2)设点P在C1上,点Q在C2上,求PQ的最小值以及此时点P的直角坐标.解析(1)C1的普通方程为+y2=1,C2的直角坐标方程为x+y-4=0.

　　(2)由题意,可设点P的直角坐标为(3 cosα,sinα),因为C2是直线,所以|PQ|的最小值即为点P到C2的距离d(α)的最小值.d(α)==2|sin(α+)-2|.当且仅当α=2kπ+(k∈Z)时,d(α)取得最小值,最小值为2,此时点P的直角坐标为(,).

　　“破题”与评注把参数方程化为普通方程,需要根据其结构特征,选取适当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方和(差)消参法、乘法消参法、混合消参法等.

　　3利用极坐标的应用

　　例3(广东2021年高三联考)在平面直角坐ì55标系xOy中,直线l的参数方程为í(t为参îy=t数),以平面直角坐标系的原点为极点,正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为ρ2=2 2ρsin(θ+)-1.

　　(1)求直线l和曲线C的直角坐标方程,并指明曲线C的形状;

　　(2)设直线l与曲线C交于A,B两点,O为坐标原点,且|OA|<|OB|,求-.ì55

　　解析(1)由í消去参数t,得y=2x.îy=t

　　由ρ2=2 2ρsin(θ+)-1,

　　得ρ2-2ρcosθ-2ρsinθ+1=0.

　　所以曲线C的直角坐标方程为x2+y2-2x-2y+1=0.

　　即曲线C是圆心为(1,1),半径r=1的圆.

　　(2)联立直线l:tanθ=2与曲线C的方程消去

　　θ,得ρ2-ρ+1=0.

　　设A,B对应的极径分别为ρ1,ρ2,则

　　ρ1+ρ2=,ρ1ρ2=1.

　　所以-=(ρ1+ρ2)2-4ρ1ρ2 4 5==ρ1ρ2 5.

　　“破题”与评注此题关键是极坐标方程的求法及其应用,重点考查了学生的转化与化归能力.在求曲线交点、距离、线段长等几何问题时,求解的一般方法是将其化为普通方程和直角坐标方程后求解,或者直接利用极坐标的几何意义求解.因此,需要学生理解极坐标中几个核心概念,比如极角极径的含义,这也是学生容易忽略的知识点,学完也容易遗忘.

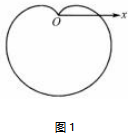
　　反馈练习(2021年云南师大附中高三模拟)心形线是一个圆上的固定一点在它绕着与其相切且半径相同的另外一个圆周滚动时所形成的轨迹,因其形状像心形而得名.如图1,在极坐标系中,方程ρ=a(1-sinθ)(a>0)表示的曲线C1就是一条心形线.以极轴Ox所在的直线为x轴,极点O为坐标原点的直角坐标系xOy中,曲线C2的参数方程为为参数),C1与C2的其中一个交点A(异于点O)在x轴上.

　　(1)求C2的极坐标方程及a;x=1+4t

　　(2)已知曲线C3的参数方程为í3(t为

　　y=+3t解析消去C2参数方程中的φ,可得(x+2)2+y2=4.又由x=ρcosθ,y=ρsinθ,所以C2的极坐标方程为ρ=-4cosθ.

　　由于C2与x轴的其中一个交点A(异于点O)的极坐标为(4,π),故4=a(1-sinπ),即a=4.

　　(2)消去C3参数方程中的t,得y=x.

　　设其倾斜角为α,则有tanα=且α∈(0,).所以C3的极坐标方程为θ=α(ρ∈R).又C1与C3相交E,O,F三点,得OE|=|ρE|=4(1-sinα)>0,|OF|=|ρF|=4(1+sinα)>0所以|EF|=|OE|+|OF|=8.

　　复习过程中首先要注重学生对基本概念与方法的学习,特别是核心概念的理解,熟练掌握基础知识与技能,从而快速“破题”,以此提升学生的逻辑推理和数学运算等核心素养,让学生学会与圆锥曲线三种方程的整合.然后要重视思想和方法的总结,比如数形结合思想、转化与化归思想和分类讨论思想.最后强化参数几何意义、极径、极角和参数方程的理解,比如类型三中利用极径的几何意义解题,大大简化了运算,解答思路也更清晰.

　　参考文献:

　　[1]方明生.坐标系与参数方程几种常见题型的解法[J].中学数学研究,2020(03):58-60.