摘要:极限思维与天体运动的契合,帮助学生实现看不到但能想到的天体运动、做不到但能悟得出的航空问题.人造卫星是学生将万有引力知识与天体运动形成理论与实践联系的最佳题材,是学生开启航空航天梦想的钥匙.高中物理教学不仅要引导学生会运用圆周运动的知识解决人造卫星的环绕问题,更要挖掘学生搞懂人造卫星发射、运行原理后的隐形教育价值.

　　关键词:极限思维;人造卫星;发射、运行与环绕

　　极限思想是用极限概念分析、解决实际问题的思维加工过程,是一种科学思维方法.借助极限思想,我们能从有限认识无限,从"不变"认识"变",从直线认识曲线,从量变认识质变,从近似认识精确.极限问题的物理思想是物理过程量的连续渐变累积;极限问题的数学思想是微积分.人造卫星发射、运行与环绕的理论探究是学生开启航空航天大门的钥匙,如果在教学过程中只引导学生对人造地球卫星轨道环绕完成公式推理应用,而对人造卫星的发射及其环绕前的运行过程少有分析,这样的物理课堂只是做了物理知识教学;如果借助人造卫星的教学帮助学生开锁航空航天的的好奇心与理论技能,这样的物理课堂是做好物理教育.

　　1极限放大思想造“人造卫星”

　　以水平抛出的粉笔为例.粉笔以初速度v0沿水平抛出,不计空气阻力,粉笔做平抛运动.学生分析

　　完成平抛运动的规律:

　　水平方向:

　　X=v0 t

　　竖直方向:

　　h=gt2

　　师:保持粉笔抛出时的高度不变,如果不断增大抛出时的初速度v0,平抛运动的水平位移X会怎么变化?

　　生:会不断增大

　　师:如果v0足够大,请同学们大胆猜想水平位移会……

　　生:水平位移指向无限远,平抛运动的曲线运动趋近沿水平方向的直线运动,即粉笔回不到地球上.

　　师:如果你拥有和这只粉笔一样大的速度v0,并随抛出的粉笔方向沿地面跟着粉笔走,以你为参考系,粉笔做什么运动?

　　生:静止

　　师:你绕地球走了一圈,粉笔呢?

　　生:粉笔绕地球转了一圈,哦,粉笔做匀速圆周运动.

　　师:同学们,此时的粉笔就不叫粉笔啦,物理学家把它叫人造卫星!

　　受平抛运动到圆周运动的极限思维启发,平抛运动可以看做是近心运动:即重力提供以速度为v0,半径近似等于地球半径R的圆周运动所需要的向心力有多余,多余的这部分重力使粉笔做竖直方向的加速直线运动,即平抛运动是匀速圆周运动和竖直方向加速直线运动的合运动.重力的作用效果分为两部分:

　　mg1=m和mg2=mɑ

　　两个分运动的运动类型:匀速圆周运动和加速直线运动.

　　当v0增大时,需要的向心力F向=m增大,提

　　供的力mg1增大,mg=mg1+mg2,mg2减小;当m增大到一定值,满足mg1=mg时,粉笔将回不到地面,围绕地球做匀速圆周运动.得出人造卫星成果发射的最小速度

　　v1==7.9km/s.

　　2极限思想造“脱轨”人造卫星

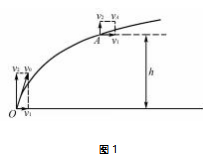
　　建构卫星发射模型:如图1所示,卫星在地面附近一次性加速获得初速度v0,进入高空轨道做匀速圆周运动.卫星离开地面的初速度v0与水平方向之间的夹角越大,卫星飞行的高度就越高.极限思维:当h趋向无穷大时,卫星从地面上发射的最小初速度v0是多少?

　　(G=6.67×10-11 N·m2/kg2,M=5.96×1024 kg,R=6.37×106 m.)理论分析:无穷远处的引力趋于零,无法提供做圆周运动所需的向心力.即无穷远高度处不能做圆周运动,取速度等于零,卫星初始动能就等于克服引力对卫星做的功.

　　WF=∫G dr=G+C

　　=-G

　　WF=0-mv=-mv

　　(当α趋近90°时,v2=v0)

　　联立两式得:

　　v0=v2=11.2 km/s

　　当发射速度大于11.2 km/s,即该物体不再是地球的人造卫星.

　　故人造卫星的发射速度7.9 km/s≤v0≤11.2 km/s.

　　3极限理论推理地球同步卫星的发射速度和发射角

　　以地球同步卫星为例,如图1,设初速度v0与水平方向成α角,同步卫星要上升至距地面高度为h0的高空做匀速圆周运动,线速度为v1,求同步卫星的发射速度?

　　(已知:G=6.67×10-11 N·m2/kg2,M=5.96×1024 kg,R=6.37×106 m,h0=3.6×107 m,ω地=7.29

　　×10-5 rad/s)

　　综合分析:同步卫星在距离地面高度为h0过A位置的面内以线速度v1,半径为R+h0做匀速圆周运动,此高度处的v2′=0,卫星受到的吸引力全部提供向心力,即

　　G=m(R+h0)ω

　　v1=(R+h0)ω地

　　同步卫星在进入圆周轨道前做离心运动,离心运动可等效为匀速圆周运动和上升过程中竖直方向上的减速直线运动.所受的引力产生两个作用效果:提供高度为h0处匀速圆周运动的向心力和改变此高度h位置处竖直方向上的运动状态.设高度为h处的卫星到地心的距离为r=R+h,竖直方向速度为v2′,所受引力为F=G,提供向心力的引力部

　　参考文献:

　　[1]吴百诗.大学物理(新版)上册[M].北京:科学出版社,2001.

　　[2]束炳如,何润伟.物理(共同必修1)[M].上海:科技出版社,2004.

　　[3]同济大学数学系.高等数学(第六版,上册)[M].北京:高等教育出版社,2007.