摘要:数形结合思想在数学学科的学习中一直占据着不可替代的地位．文章将在阐述数形结合思想对学生思维培养和解题方法重要性的基础上，具体分析数形结合思想在各类数学题目中的解题策略.

　　关键词:数形结合;初中数学;解题

　　数学的抽象性和复杂性让学生心生恐惧，使他们丧失学习数学的信心和热情．数形结合使数字关系可以和直观图像发生有效转换，不易理解的数据变得更加形象透明，学生可以从图像中观察数据，也可以将数据构建成图像．在解题过程中，应用数形结合思想能使学生们更加深入地理解题目中的有效信息和关键所在，提高学生探索问题、解决问题的热情和兴趣，促进学生形成高效的思维方式和解题方法，提高学生的认知理解水平和逻辑思维能力.

　　1代数问题几何化

　　代数问题是初中数学中最常见、最重要的题型之一，大多数情况下在选择题和填空题部分出现，也会与其他问题结合以应用题的形式出现．在选择题和填空题部分，学生不应该耗费太多时间，因此学生需要掌握答题技巧，将部分代数问题几何化，既能够缩短计算过程和解题时间，也能够提高答案的准确性．教师应传授数形结合技巧，帮助学生搞清问题的本质，简化代数问题，切实提高解题效率和质量.

　　1．1构造点之间的关系

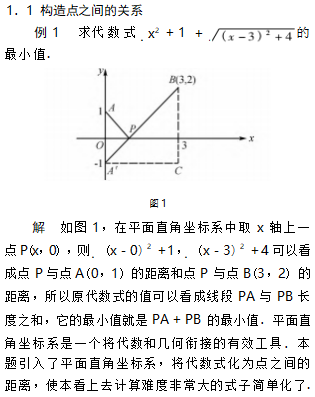
　　1．2构造图形

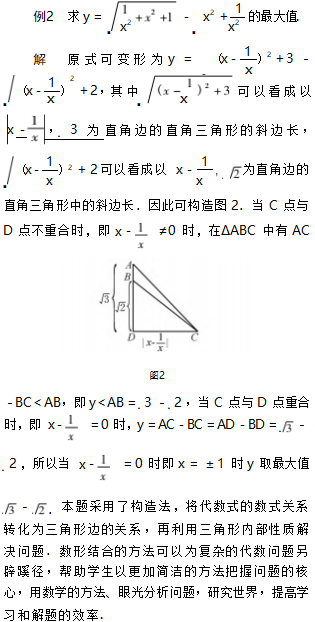
　　2方程不等式图像化

　　方程和不等式问题是中考数学的必考内容．在解决方程和不等式问题时，数形结合的方法至关重要，通常需要结合函数图像使题干的含义更加直观明确．数学习题中，有很多综合性较强的数学题都涉及到了函数与其他知识点的结合．教师在日常教学中要提高学生绘图的动手实践能力，教授学生如何快速画出一幅简单明了的函数图像，引导学生运用函数图像巧妙解决相关数学问题．当遇到与不等式和方程相联系的题目时，学生可以借助函数图像解决解的取值范围以及方程的根等问题.

　　3平面几何代数化

　　爱因斯坦曾说:“单凭传统的逻辑思维而想有所发现是困难的甚或是不可能的．”平面几何在初中数学教材中占据了很大篇幅，旨在培养学生的逻辑思维，提升他们的推理能力．相比于纯几何解法，平面几何的代数解法往往更加简洁，思路更加明确.在解决几何问题的过程中，初中生能够在逻辑的演绎和一步步地推理中对平面几何知识有综合的应用和把握，也能够提升自己数形结合解决问题的能力.

　　一些几何问题具有条件隐晦、技巧性强的特点，很多学生遇到这种问题往往像无头苍蝇，无从下手．与其作很多的辅助线，还不如将平面几何问题代数化，这个方法有助于形象思维和想象能力较弱的学生解决平面几何问题，使解题思路更加明晰.

　　4应用题用数形结合求解

　　将数学知识应用到具体问题中一直是学习数学的最终目的之一．然而，应用题相比于填空题与选择题，难度更高，计算更复杂，因此具体的应用题一直是教师感到头疼，学生害怕遇上的题目．如果学生不能在计算的过程中融入自身的理解，则解应用题就可能变得非常难懂和困难．对于初中学生，运用数形结合的方法解决应用题，既有利于学生对题意的理解使解题过程直观化，提高解决数学问题的能力，还有利于减轻学生对应用题的抗拒、抵触等消极情绪，从本质上激发学生学习数学的好奇心和探索欲，使枯燥的解题过程具有吸引力.

　　4．1引入数轴、平面直角坐标系解决应用题

　　数轴是数形结合的基础和平面直角坐标系的初始形态，数轴部分也是初中数学教学中的基础知识点，可以把点和线更加直观地反映在数轴上，使学生们对负数、零、正数、相反数、绝对值等概念获得更加清晰的把握，在解决题目中引入数轴也能使题目化繁为简．教师需要引导学生熟悉将数轴引入题目的技巧，利用数轴比较数的大小，划分数集范围，培养数形结合的思维习惯.

　　4．2概率统计应用题

　　虽然初中数学课程仅包含基础的概率学和统计学知识，但是这对于刚刚接触概率统计相关知识的初中学生来说依旧很难上手，难度较高，这使得很多学生在学习以及做题时都困难重重，有很重的思想包袱．在教学中，教师要关注学生吸收和理解知识的状况，将数形结合思想逐渐渗透进概率和统计的学习之中，注重培养学生的数学逻辑和思维，帮助学生在解题中将知识和方法融会贯通，这对学生后续学习统计知识意义重大［1］.

　　参考文献:

　　［1］韦秀美，冯吉伟．“数形结合”思想在初中数学解题中的运用技巧［J］．中学数学，2022(08):75－77．