摘要:本文从人教版高中物理新教材必修一中第37页提出的一个思考问题出发，利用数学手段透视其本质，并展示其数学建模的过程.

　　关键词:凸函数;数学建模

　　人教版高中物理新教材必修一中第37页有一个思考题:世界上第一条商业运行的磁悬浮列车———“上海磁浮”，已于2003年10月1日正式运营．据报道，上海磁浮线路总长33 km，一次试车时全程行驶了约7 min 30 s，其中以430 km/h的最高速度行驶约30 s．磁悬浮列车的行驶速度比汽车快得多，是不是它的加速度也会很大?学过这一章后请你根据报纸上的数据，再按照实际情况给出一些简化的假设，自己尝试着估算它的加速度.

　　没有想到的是物理教师竟然无法解决该问题，于是他们将该情境化问题按照他们的思路分析判断、简化抽象．最后转换为一个他们自认为很得意的抽象化的问题:某物体从静止开始做匀加速运动，在3．5 min的时间内速度达到430 km/h，求物体的加速度．当然如果这样处理，问题立马变得简单，但是这样处理后的问题已经不是教材中提出的思考问题了．因此本文作者认为这样处理存在严重问题，我与物理老师交流，他们却不以为然，认为可以这样估算，不然就无法解决．看来这种错误在物理学科中普遍存在，因此有必要提出来，与大家进行商讨.

　　为了叙述方便，我们首先定义凸函数:设f为定义在区间I上的函数，若对I上的任意两点x1、x2和任意的实数λ=(0，1)，总有

　　下面就这个问题进行分析，首先我们根据题意可以得到一个速度(km/min)函数:

　　如果f(t)，g(t)是线性函数，那么我们可以画出函数v=h(t)的图像，如图1所示.

　　显然当a=3．5时，就是物理老师所给出的模型.

　　我们知道这个梯形的面积就是磁浮线路总长，现在我们计算一下这个梯形的面积

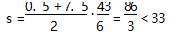
　　由此可以看出，两端设计为匀加速运动，无论a为何值，都不能满足条件.

　　由于梯形的面积s＜33，所以函数f(t)应该设计为上凸函数(当然函数g(t)也可以设计为上凸函数，为了简单起见我们只考虑函数f(t))．由于高一学生没有学过定积分，所以我们首先将f(t)设计为两段一次函数．如图2所示.

　　这表明点(b，c)在直线6av=43t+52上，即平行于OA的一段线段MN内，不包括端点M、N．如图3所示.

　　假设列车运行的加速度的绝对值越小列车运行的稳定性越好，那么从列车运行的稳定性角度考虑，加速度的最大绝对值应该尽量小，假设此时a=3．5，那么点(b，c)越靠近点M时，其加速度的最大绝对值越小，首先我们计算一下点M的坐标.

　　下面我们设想函数f(t)的图像是上凸曲线，如图4所示.

　　如果把线路总长33 km改为26 km，那么得到下面问题:

　　某磁浮线路总长26 km，一次试车时全程行驶约7 min 30 s，其中以430 km/h的最高速度行驶约30 s．请根据实际情况给出一些简化的假设，尝试估算它的加速度.

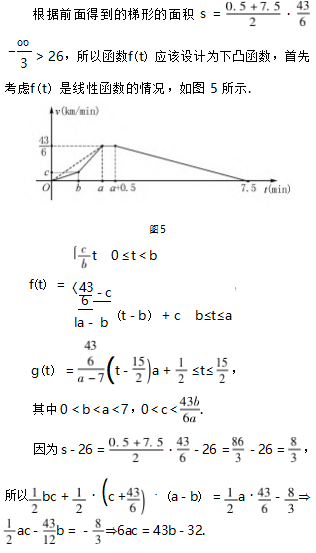
　　这表明点(b，c)在直线6av=43t－32上，即平行于OA的一段线段MN内，不包括端点M、N．如图6所示.

　　同样从列车运行的稳定性角度考虑，加速度的最大绝对值应该尽量小．假设此时a=3．5，那么点(b，c)应该靠近点N为好，如图6首先我们计算一下此时点N的坐标.

　　下面我们设想函数f(t)的图像是下凸曲线，如图7所示.

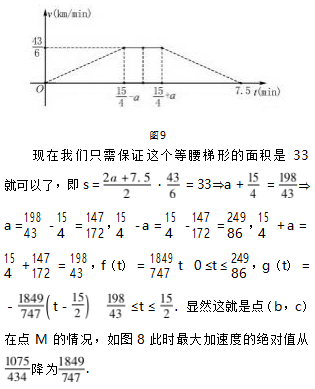
　　现在回到我们的初始问题，通过前面的解析我们知道，在满足问题前提的条件下，要使列车运行在最佳状态，还是匀加速状态比较好，同时保证加速度的最大绝对值越小越好．因此在两段对称的情况下是最好的，如图8所示.

　　最后我们将问题改造，得到这样的问题:

　　某磁浮线路总长33 km，最高时速是430 km/h，全程行驶时间是7 min 30 s，请问如何设计加速度使得列车运行最稳定.

　　根据前面的解析我们知道列车运行稳定，还是匀加速状态比较好，同时保证加速度的最大绝对值越小越好．因此在两段对称的情况下是最好的，如图9.

　　参考文献:

　　［1］人民教育出版社，课程教材研究所，物理课程教材研究所．普通高中教科书·物理［M］．北京:人民教育出版社，2020．