摘要:以向量、不等式等为知识交汇背景来命制抛物线试题，常常是高考命题的一大特色，这类问题需要特别关注对向量、不等式等语言的转化．本文对贵阳第一中学2022届最后一次模拟考试中的一道抛物线考题的变式和拓展进行探究.

　　关键词:抛物线;试题;变式拓展

　　1考题呈现

　　2考题分析

　　解答本题，首先利用点到直线距离公式求p的值，从而得到Γ的方程，然后将Γ上三点A、B、C满足的关系++=0，即F是ΔABC的重心，转化为三点坐标之间的关系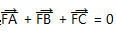，再进一步运用抛物线及均值不等式等相关知识等进行演算、推理，作出判断．本题考查抛物线方程、几何性质及直线与抛物线的位置关系等知识及抛物线与向量、不等式的交汇，考查数学抽象、逻辑推理、直观想象和数学运算等数学核心素养.

　　3考题解答

　　点评解法2在求得抛物线方程和三点坐标关系的基础上，利用三点在抛物线上得到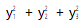的值，然后运用反证法进行推理，利用重要不等式得出矛盾，从而作出判断．反证法是推理证明的一种重要方法，也是高考常考的证明方法，它不是去直接证明结论，而是先否定结论，在否定结论的基础上，运用正确的推理导出矛盾，从而肯定结论的真实性，充分体现了数学抽象和逻辑推理数学核心素养的渗透和运用．解法2是一种颇有创意的方法.

　　4变式拓展

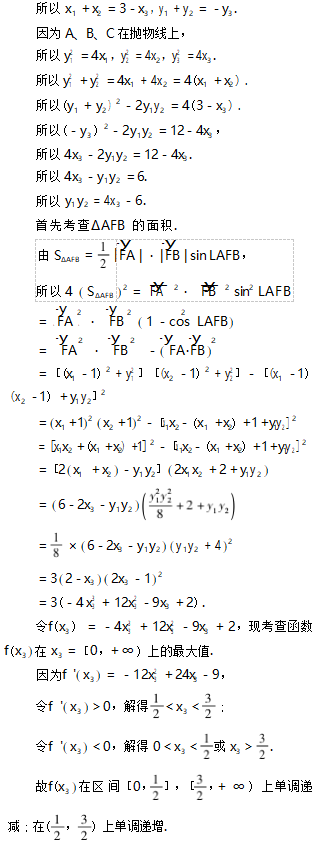
　　通过基本性质、定理、公式推导出来并具有推广应用的结论性质我们称之为“二级结论”，本文问题拓展中归纳的结论就是典型的“二级结论”．这些“二级结论”往往散落在课本例、习题中，或一些较为通用的参考书中，或老师的讲义中，其核心在于帮助学生在考试中迅速利用这些结论快、准、狠地解答一些问题，以实现分数的快速增长.同时，“二级结论”不仅对学生的解题有很好的指导作用，而且对演算结果也有精确的验证作用.因此，无论是同步教学还是在高考复习中，要常态化地指导学生通过对一些典型问题的探讨和拓展，及时归纳、总结出一些常用的“二级结论”，这对于学生解题能力的提高和数学素养的提升是颇有裨益的.

　　参考文献:

　　［1］中华人民共和国教育部．普通高中数学课程标准(2017年版2020年修订)［M］．北京:人民教育出版社，2020.