摘要:本文采用六种方法对一道直线与圆锥曲线位置关系问题进行一题多解.

　　关键词:圆锥曲线;一题多解;解析法

　　1试题呈现

　　2思路分析

　　第(1)小题以椭圆为载体，主要考查椭圆的标准方程及简单几何性质;考查运算求解能力、直观想象能力等;考查数形结合思想、函数与方程思想、化归与转化思想等;考查直观想象、数学运算等核心素养．根据图形，选择建立以O为坐标原点，椭圆C的长轴、短轴所在直线分别为x轴、y轴的平面直角坐标系，然后设椭圆的长半轴为a，短半轴为b，焦半径为c，根据题意求得a、b，从而求得C的标准方程.

　　第(2)小题以圆为载体，主要考查直线与圆、椭圆的位置关系，平面向量等基础知识;考查运算求解能力、逻辑推理能力、直观想象能力和创新能力等;考查数形结合思想、函数与方程思想、化归与转化思想等;考查直观想象、逻辑推理、数学运算等核心素养．根据题意，可以得到直线AB与圆O相切，并通过对称性，可以猜测以AB为直径的圆过点O，然后加以证明．可以把要证结论转化为证明OA⊥OB，再转化证明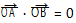，当直线AB的斜率不存在时，验证较为容易，当直线AB的斜率存在时，可以设直线AB的方程为y=kx+m，也可以设直线AB与圆O相切于点M(x0，y0)，得到以点M的坐标表示的直线AB的方程，然后联立直线AB与椭圆C的方程，结合韦达定理加以证明;也可以通过证明OA 2+OB 2=AB 2，得到OA⊥OB;还可以通过设直线AB的方程为y=kx+m，然后联立直线AB与椭圆C的方程，求得以AB为直径的圆的方程，再确定定点.

　　3多维探析

　　3．1第(1)问解析

　　解析以O为坐标原点，椭圆C的长轴、短轴所在直线分别为x轴、y轴，建立平面直角坐标系，如图1.

　　3．2第(2)问解析

　　解法1因为直线AB与以OA为直径的圆的一个交点在圆O上，所以直线AB与圆O相切.

　　解法2因为直线AB与以OA为直径的圆的一个交点在圆O上，所以直线AB与圆O相切.

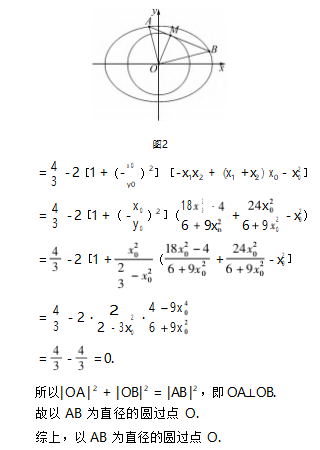
　　解法3因为直线AB与以OA为直径的圆的一个交点在圆O上，所以直线AB与圆O相切.

　　解法4因为直线AB与以OA为直径的圆的一个交点在圆O上，所以直线AB与圆O相切.

　　解法5因为直线AB与以OA为直径的圆的一个交点在圆O上，所以直线AB与圆O相切.

　　解法6因为直线AB与以OA为直径的圆的一个交点在圆O上，所以直线AB与圆O相切.

　　参考文献:

　　［1］杨苍洲，王志良．探究一道试题的命制心路［J］．数学教学，2016(01):32－33.

　　［2］杨苍洲．2014年天津卷理科压轴题命题手法探究［J］．高中数学教与学，2020(03):33－34.

　　［3］杨苍洲．几何直观素养下的含参数问题的速解策略［J］．数学通讯(下半月)，2020(06):38-39，47．