摘要:文章给出了比较大小问题的求解策略:作差(商)比较法、数形结合(几何意义)、借助中间值、利用不等式性质和构造函数法.

　　关键词:比较大小;同构;数形结合

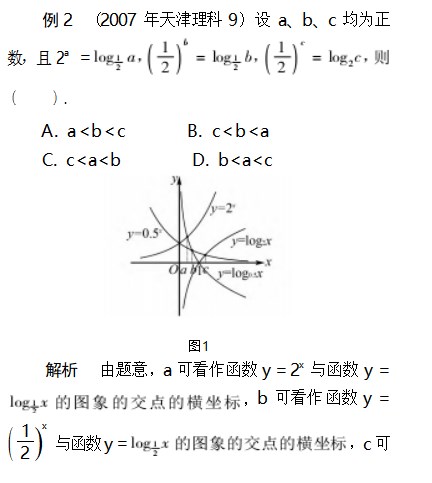
　　比较大小问题是高中数学中常见的题型，也是高考中常考常新的一类问题，近年来的高考对这类问题的考查有加大难度的倾向．这类问题通常以不等式的基本性质为主要依据，以基本不等式、函数的图象和性质为主要工具，通常采用比较法、中间值法、数形结合法、同构法等来解答，综合性较强，涉及不等式、函数、代数变形等多方面的数学知识及数形结合、转化与化归的数学思想方法，具有涉及面广、立意新、角度新、解法灵活多样等特点，能够从多方面考查同学们分析问题与解决问题的能力，充分培养和发展同学们的逻辑推理、数据处理、直观想象、数学抽象等核心素养.

　　0，从而b＜c＜a，故选B.

　　点评作差(作商)比较法是比较大小问题的基本方法，作差(作商)后进行合理的变形化简是求解的关键，这里不再详谈.

　　2数形结合或几何意义

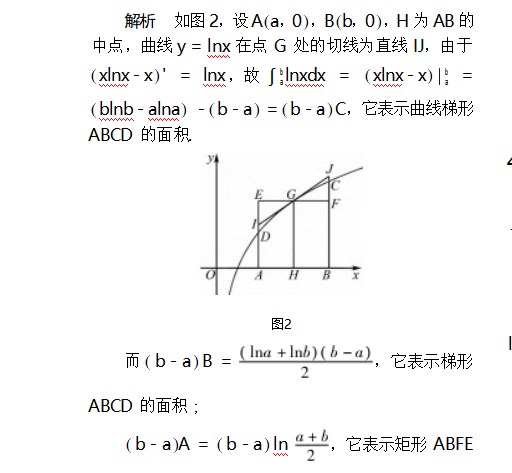
　　的面积，又显然SΔGFJ=SΔGEI，故矩形ABFE的面积和梯形ABJI的面积相等.

　　由图易知梯形ABJI的面积＞曲线梯形ABCD的面积＞梯形ABCD的面积.

　　即(b－a)A＞(b－a)C＞(b－a)B.

　　故A＞C＞B.

　　点评常见的几何意义有:斜率、面积、长度、(两点、点线)距离等．可以根据所给表达式的结构特点，发掘其隐含的几何意义来求解.

　　3中间值法

　　点评最常见的中间值有0和1，在具体问题的求解中，要根据实际情况选择合理的中间值.

　　4借助不等式性质或放缩

　　点评解法中的不等式是怎么想到的?其实是

　　5构造函数

　　5．1同构法构造函数

　　数学中的同构式是指除了变量不同，而结构相同的两个表达式．许多比较大小的问题，通过等价变形，可以转化为同构式，然后构造函数，利用函数的单调性来求解，同构法是近些年高考的热点.

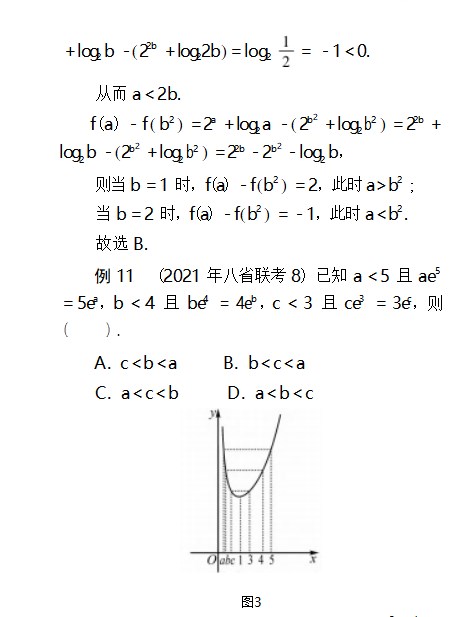
　　点评本题中a、b、c非常接近，又涉及到对数和根式的运算，直接很难比较，三个数中的1．01、1．02、1．04非常接近，因此引入x=0．01构造函数来比较大小，比较巧妙!读者也可以用这种方法解决本文中的例8.

　　从以上问题可以看出，比较大小的问题求解思路灵活多样，需要我们从不同角度去观察、分析和思考问题，正因为此，这类问题比较受命题者的青睐.因此，在平时的练习中，我们要尽量从不同的角度去思考问题，一题多解，举一反三，多总结，熟练地解决此类问题.

参考文献:

　　［1］闫伟．例说指数与对数比较大小问题的求解策略［J］．高中数理化，2020(Z2):30－32.