摘要:对2022年高考全国甲卷一道含容导杆问题进一步定量研究，求出电容器两极板电荷量q、金属杆中的电流i以及金属杆的速度v随时间的变化规律，为本题的定性解答提供理论依据，从而体现高考命题的科学性.

　　关键词:反电动势,最大速度,电动机,发电机,线性齐次微分方程

　　1对原题的分析与解答

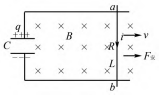
　　(2022年高考全国甲卷第20题)如图1，两根相互平行的光滑长直金属导轨固定在水平绝缘桌面上，在导轨的左端接入电容为C的电容器和阻值为R的电阻．质量为m、阻值也为R的导体棒MN静止于导轨上，与导轨垂直，且接触良好，导轨电阻忽略不计，整个系统处于方向竖直向下的匀强磁场中．开始时，电容器所带的电荷量为Q，合上开关S后()

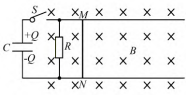
       A．通过导体棒MN电流的最大值为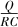

　　B．导体棒MN向右先加速、后匀速运动

　　C．导体棒MN速度最大时所受的安培力也最大
       D．电阻R上产生的焦耳热大于导体棒MN上产生的焦耳热

　　分析与解答开始电容器两端电压等于，电容器相当于电源，电容器通过导轨、电阻R及金属杆构成的回路放电，磁场对通有电流的金属杆施加向右的安培力，使金属杆从静止开始向右做加速运动．金属杆在磁场中运动切割磁感线所产生的感应电动势是一反电动势，它阻碍电容器通过金属杆放电．设某时刻t电容器两极板电荷量为q，则其两端电压为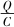，此时金属杆中的电流为i，金属杆获得的速度为v，由牛顿第二定律及欧姆定律F安=BiL=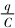ma，－BLv=iR,电容器在放电q↓,金属杆在加速v↑,故金属杆中的电流i↓,金属杆的加速度a↓,当a=0时，金属杆达到最大速度vm，设此时电容器两极板电荷量为qm，则－BLvm=0．当开关闭合的瞬间，q=Q，v=0，通过导体棒MN电流的最大值为im=，故A正确．导体棒MN速度最大时，a=0，F安=0，故C错误．导体棒MN速度最大时，金属杆中的电流i=0，=BLvm，但电阻R两端仍有电压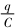，仍然有电流通过电阻，电容器会继续通过电阻放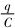＜BLv，导体棒中电流反向，安培力反向，导体棒会继续减速，电阻R和导体棒上会继续产生焦耳热，由能量守恒定律可知，电容器的电能最后将全部转化为两部分电阻的焦耳热，所以终极状态必定为电容器极板电荷量为零，导体棒速度为零，导体棒是先加速后减速，故B错误．导体棒在加速阶段，＞BLv，由于反电动势的存在，导体棒中的电流i=BLv小于电阻R中的电流i'=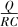，电阻R上产生的焦耳热大于导体棒MN上产生的焦耳热;导体棒在减速阶段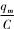，＜BLv，导体棒中电流反向，电容器的电流和导体棒的电流都流经电阻R,此过程也是电阻R的电流较大，电阻R上产生的焦耳热大于导体棒MN上产生的焦耳热，故D正确.

　　点评注意如果没有旁路电阻R,导体棒最终会以最大速度匀速运动，这种情形B选项才是对的，死记硬背的话刚好掉坑．旁路电阻的存在告诉我们整个电路一直有焦耳热产生，同时考查了电动式和发电式导体杆，物理过程比较复杂，状态变化过程中变量比较多，要求学生要有较高的动态分析能力.另外，解决本题时综合应用了电磁学中的有关规律和力学中的有关规律，比如电磁学中的欧姆定律、左右手定则，力学中的牛顿运动定律、能量守恒定律等，而且本题还涉及到临界问题，极值问题，解题的关键是能抓住状态变化过程中变量“变”的特点和规律，从而确定最终的稳定状态，这种题型对培养学生综合应用知识解决问题的能力具有独特的意义，有较高的区分度，体现了较强的选拔功能.
          2对原题的变式研究
           如图2所示，如果没有旁路电阻，导体棒最终会以最大速度匀速运动，求导体棒能够获得的最大速度及整个过程回路中产生的焦耳热.

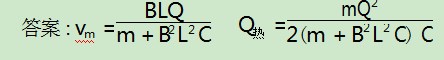
      3对原题的定量研究

　　3．1问题的提出

　　本题解答中我们根据能量守恒定律得出终极状态为电容器极板电荷量为零，导体棒速度为零，这只是定性分析，得出的结论不一定可靠．下面我们对此题进一步定量研究，求出电容器两极板电荷量q、金属杆中的电流i以及金属杆的速度v随时间的变化规律，为本题的定性解答提供理论依据，从而体现高考命题的科学性.

　　3．2问题的解决

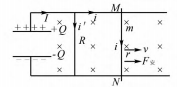
　　为使问题更一般化，假设导体棒的电阻为r，规定图3中所示方向为各物理量的正方向(如i＜0，则F安=BiL＜0，表示电流反向，安培力反向)

       所以终极状态必定为电容器极板电荷量为零，导体棒速度为零，证毕!　通过对此道含容导杆问题的定量研究可知，原定性解答得出的结论与定量研究得出的结果完全相符，为本题的定性解答提供了理论依据，从而体现了高考命题的科学性.

参考文献:

　　［1］黄尚鹏．电磁感应现象中复杂的单导体杆问题［J］．物理教学，2013(09):59－63.

　　［2］黄尚鹏．对电磁感应现象中两个复杂的导体杆问题的深入研究［J］．物理教学探讨，2013(12):32－34．BLQ