摘 要：培养初中生的物理解题能力，是初中物理教学的重要组成部分.鉴于物理学科特点，面 对复杂的物理问题，学生唯有灵活运用多种解题方法，才能逐渐突破思维的局限，实现物理题目化 繁为简、化难为易，真正提升学生的解题效率.本文基于初中物理极值解题法，围绕其内涵和解题实 践进行论述，并由此提出具有针对性的教学建议，以期为教师的教学工作提供一定的参考.

　　关键词：初中物理,极值法,解题

　　物理知识理论性强、涉及学科广，对学生的知 识、思维要求比较高.尤其是“ 物理核心素养”的提 出，要求教师在组织课堂教学时，不再局限于理论知 识的灌输，更加关注学生的物理思维、问题解决能 力，真正实现学生的全面发展.解题作为初中物理教 学的重要组成部分，不仅考查物理理论知识掌握情 况，也反映了知识的迁移和应用能力.鉴于此，在日 常物理教学中，积极渗透物理解题方法，引导学生在 快速准确解题过程中促进知识内化、思维发展，已经 成为当前物理教学的重要组成部分.

　　1 初中物理极值解题法教学概述

　　极值法又被称之为极端假设法、极限法等.极值 法就是将问题中某个变量取最大值、最小值，或者某 一个定值时，通过分析所得出来的结论，最终完成问 题的解答.在初中物理学习中，伴随着所学内容的增 加，以及题目难度的加大，当常规解题方法受限时， 可巧妙运用极值法，在打开学生解题思路的同时，也 实现了物理题目化繁为简、化难为易，使得物理解题 更加高效.同时，在运用极值法解题的过程中，进一 步开阔了学生的思维，有助于帮助其形成跨学科思 维，使其意识到极值解题法不仅仅局限于物理学科 中，还可灵活应用到其他学科中，真正实现了学生的全面发展.因此，从这一角度上来说，积极开展极值法 教学，是提升学生物理解能力的必然选择，更是促进学 科素养的有力途径[1] .

　　2 极值法在初中物理解题中的应用

　　2. 1 极值法解决液体压强问题

　　“ 液体压强”是初中物理中非常重要的知识点， 也是考试的重点.针对这一类型的题目，如果按照常 规解题思维，将面临着繁琐的步骤.而通过极值法， 则可巧妙避开常规解题思路中的诸多物理量分析， 直接得到答案，极大地提升了学生的解题效率.

　　例 1 如图 1 所示，有两个完全相同的量筒，其 中一个量筒中盛有水，另外一个量筒中盛有酒精.已 知酒精和水的质量相同，且两个量筒中 M、N 到量筒 底部的距离也相等.假设两点处的液体压强分别为PM 、PN . PM 与 PN 的大小关系正确的是( ) .

　　A. PM < PN B. PM > PN

　　C. PM = PN D. 无法确定

　　解析 按照常规的解题思路，因为 M、N 到量筒底 部的距离相等，则两种液体体积相等.因为水的密度大 于酒精的密度，则 M 点下方水的质量大于 N 点下方酒 精的质量.又因为两个量筒相同，则横截面积相等.即

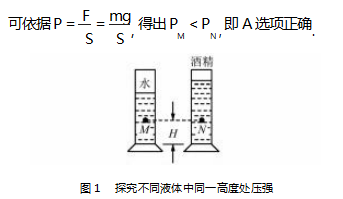
　　但是巧妙运用极值法，可简化解题过程，避免诸 多物理量分析.在极值法解题中，由于题目中没有给 出 M、N 两点的位置，只说明两者到量筒底部的距离 相等.此时，即可将 M 取在水面上，此时水所产生的 压强为 0;而对于 N 点来说，由于其到量筒底部的距 离与 M 点相同，则 N 上方依然存在酒精，此时其压 强显然大于 0. 由此可得出 PM < PN .

　　综合上述两种解题思路不难发现，常规解题思 路虽然能够获得正确的答案，但学生在解题时，需要 围绕液体体积、质量、压强等物理量展开精准地分 析，方可得到正确的答案.而通过极值法则可巧妙避 开这些繁琐的分析，进一步提升了物理解题效率.

　　2. 2 极值法解决杠杆平衡问题

　　“ 杠杆平衡”是初中物理中一个常见的考点，题 目虽然非常多，但基本上都是判断其平衡方向.经解 题实践证明，适当运用极值法，使得题目分析更加透彻，解题速度也随之提升.

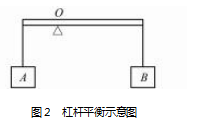
　　例2 如图 2 所示，杠杆处于平衡的状态下，如果将图中的物体 A 和物体 B分别向支点的方向移动相同的距离，则杠杆会出现的状态是( ) .

　　A. 杠杆仍然平衡

　　B. 不能平衡，向 A 端倾斜

　　C. 不能平衡，向 B 端倾斜

　　D. 条件不足，无法判断

　　解析 按照常规的解题思路，学生需要结合相 关的公式进行判断，即：mA gL1 = mB gL2 , L1 < L2 , 由此 即可推断出 mA > mB , 假设物体 A 和物体 B 分别向 支点移动 ΔL , 则物体 A 和 物 体 B 的 力 矩 分 别 为mA g( LA - ΔL) 、mB g ( LB - ΔL ) , 又 因 为 mA gΔL >mB gΔL , 则有 mA g( LA - ΔL) < mB g( LB - ΔL) , 即：杠杆会出现向 B 端倾斜的现象，选项 C 正确.

　　而通过极值法则可有效避免“ 力矩变化关系 ” 分析，将原本复杂的问题简单化，即：由于题目中并 未直接给出规定的移动距离数值，学生可任意取值. 此时，即可将物体 A 直接移动到 O 点，此时物体 A 的力 臂、力矩为 0;而对物体 B 来说，其力臂和力矩明显不为 0. 此时杠杆必然会向 B 端倾斜，选项 C 正确[2] .

　　2. 3 极值法解决浮力问题

　　“ 浮力”也是初中物理的重要知识点，也是常考 的内容之一.在这一部分知识中，部分问题学生按照 常规的思维很难完成.而运用极值法可快速求解.

　　例 3 将一个 20N 的空心铁球浸入到水中，则 铁球会在水中出现的状态是( ) .

　　A . 上浮 B . 下沉 C . 悬浮 D . 以上均有可能

　　解析 这一题目条件比较少，有关铁球体积、空 心部分体积都没有提到.此时，如果常规的解题思 路，根本无法对铁球的状态进行判断.运用极值法进 行分析：由于铁球空心部分体积未知，因此本题目可 分为三种情况：其一、铁球空心部分体积比较大，此 时铁球一定处于上浮的状态;其二，铁球空心部分体 积比较小，此时整个铁球类似于实心状态，必然会出 现下沉的状态;其三，空心部分体积恰好位于某一个 数值中，此时就可能出现悬浮的状态.因此，综上所 述，本题目的正确答案为 D 选项.

　　例 4 如 图 3所 示，一 个 密 度 均匀的木板漂浮在水面上，如果在水面虚线处将其截掉，则剩余的木块会出现什么样的变化?

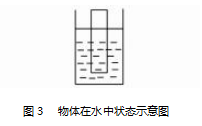
　　解析 在本题目中，如果按照常规的思维进行 解题，需要先对水中的木块进行受力分析.之后，结 合木块截掉前后的受力分析结果，得出浮力与木块 的重力相等，即 F浮 = ρ水 gV排.根据这一公式，木块 截取之后，木块排水的重力大于自身的重力.截取之 后，新木块重力大于浮力，自然会出现下沉现象.

　　鉴于常规解题中的繁琐步骤，可充分利用极值法，将题干中的信息进行扩大，使其变“将水面以下的 木块截去”.此时，木块的排水量体积为 0 , 则木块在水 中受到重力的作用，自然会出现下沉的现象[3] .

　　2. 4 极值法解决电学问题

　　电学是初中物理的重要组成，在解答这一部分 问题时，由于初中生初次接触电学知识，理论知识掌 握情况不佳，无法精准把握电流、电阻和电压之间的 关系.尤其是当电路问题中出现电阻串联、并联、滑 动变阻器时，就给学生的解题带来了极大的困难.面 对这些问题，即可巧妙融入极值法进行解答.

　　例 5 如图 4 所示，在本电路中，A 、B 两盏灯均 可发光.如果将滑动变阻器 R0 的滑片向左移动.此 时，对 A 、B 两盏灯的亮暗变化情况进行判断.

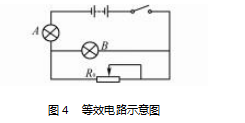
　　解析 结合电学知识，当滑动变阻器 R0 的滑片 向左移动时，致使 B 和滑动变阻器构成的并联电路 中总电阻逐渐减少，则 B 灯出现了逐渐变暗的现 象.而对于 A 灯来说，则因为回路中总电阻减少，导 致其电流增加，A 灯的逐渐变亮.在常规解题思路中， 学生必须要按照动态的原则进行分析，对于初中阶段 的学生来说，存在一定的难度.

　　鉴于此，借助极值法进行解答：由于题目中并未 明确说明将滑片移动何处，按照极值法的内涵，将其 滑到最左边.此时在整个电路中，B 灯就会出现短路完 全熄灭的现象.而 A 灯则会变得更亮.如此省去了动态 化的分析，使得解题难度降低.可见，在本题目中，通过 极值法的应用，直接揭示出问题的本质，在提升学生解 题效率的同时，也促进了物理思维的发展[4] .

　　3 初中物理极值解题法教学启示

　　结合初中物理解题实践证明，通过极值法在课 堂上的应用，实现了物理问题由繁到简、由难到易， 真正提升了学生的解题效率.鉴于此，教师在组织课 堂教学时，应通过有意识地引导，强化学生极值法解 题意识，提升极值法解决问题的能力.首先，基于课 堂教学引导学生利用极值法.在培养学生运用极值 法解题时，不仅要加强基础知识教学，还应为学生提 供一些相关的例题，通过带领学生在极值法解决实 际问题中，逐渐掌握这一解题技能;其次，加强极值 法解题联系.学生的解题能力并非一蹴而就，唯有经 过一定的练习，才能在训练中完成极值法解题技巧 的内化和应用.在日常解题教学中，不仅仅要在课堂 上给学生提供大量的例题，还应在教学之余为学生 布置针对性的练习，以便于学生在反复训练中，掌握 极值法解题的要领;最后，加强题目类型总结，促使 极值法灵活运用.初中物理知识点繁杂，且题目类型 比较多，极值法在不同题目的应用也有所不同.在日 常初中物理解题教学中，还应充分发挥教师的引导 作用，围绕不同题目类型进行归类和极值法解决力 学问题、极值法解决电学问题、极值法解决压强问题 等，促使学生在归类分析中，真正掌握这一解题技巧 的内涵，并促使其灵活应用[5] .

　　综上所述，极值法是解决初中物理问题的重要 方法之一，将其应用到物理解题中，真正促进了物理 解题由繁到简、由难到易，有效避免了解题过程中诸 多物理量的分析，显著提升了学生的解题效率.鉴于 此，初中物理教师在日常教学中，应基于极值法的内 涵，将其灵活应用到不同类型的题目中，使得学生在 极值法的辅助下，缩短解题时间，并开阔自身的解题 思维，真正满足学科素养下的物理解题需求.

参考文献：

　　[1] 赵旭林.极值法在初中物理解题中的应用[ J] .数理化解题研究，2022(05) : 109 - 111 .

　　[2] 陈胤.极值法在初中物理教学中的应用[ J] . 湖南中学物理，2020 , 35(12) : 25 - 26 + 46 .

　　[3] 卢燕.极值法在初中物理解题中的应用[ J] . 中 学物理教学参考，2020 , 49(04) : 73 .

　　[4] 石磊.运用极值法与赋值法解决电学问题的能 力的研究[ J] . 中学生数理化( 教与学)，2019 (10) : 90 .

　　[5] 顾俊文.极值法在初中物理解题中的应用[ J] .文理导航( 中旬)，2019(04) : 40 - 41 .