摘 要 : 平面向量是高中数学的重要板块之一.本文是在教学时从学生的疑问中引发的思考， 并在此基础上寻求一题多解，发散思维.

　　关键词 : 向量,投影,不等式,判别式,最值

　　该题来源于学生的提问，问题是这样的 : 已知平 面向量 a，b，c( c≠0) 满足|a | = 1.| b | = 2.a ·b = 0. ( a-b) ·a = 0.记向量 d 在向量 a，b 方向上的投影分别为 x，y，向量 d-a 在向量 c 方向上的投影为 z， 则 x2 + y2 + z2 的最小值为多少?

　　评析 我们首先来看一下甲同学的方法，他主 要利用 a ·b = 0.且通过两个向量的模长已知，设出 了向量的坐标，将 z 用 x，y 的关系表示出来，于是 x2 + y2 + z2 只与 x，y 有关，从而达到“降元”的目的，紧 接着，将代数最值问题转化为几何距离问题，典型的 利用几何问题解决代数最值问题，其中转化过程中的想法比较新颖独特，可以感受到甲同学的发散思 维能力较强.乙同学的解法也是利用向量的坐标表示，也用x，y 的关系式表示出了 z，也用到了“消元”思想.

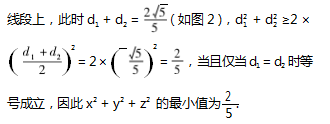
　　在高中数学教 学 过 程 中，数学老师应该多思 考如何培养学生的发散思维能力，这 个 对 学 生 今 后的发展有着举足 轻 重 的 影 响.针对这题已有的 解法，进一步探究思考新的解决方法，通 过 一 题 多解 来 培 养 、发散学生的思维能力，打 通 知 识脉络.

　　另解 1 ( 利用向量不等式) 前面过程与乙同学 的方法类似，这里从 z 的代数式给出进一步研究 : z

　　评析 该解法主要是通过引进向量 m，n，然后 利用向量不等式来加以解决，该向量不等式的本质 是柯西不等式，柯西不等式是基本不等式的延伸，它 的形式很优美，结构很巧妙，是求解最值问题的有效 工具.当不等式中有多个量具有平方和的造型时，采 用柯西不等式来推理求解，往往能达到事半功倍的 效果.

　　评析 此解法主要是多次利用判别式法，对代 数式的值设 t 后，通过变形转化得到关于 x 的一元 二次方程有解问题，使用“Δ”法后，变形得到关于 y 的一元二次不等式有解问题，再次使用“Δ”法后，最 终得到参数 t 的最值.这里得要注意在利用“Δ”法 求函数最值时，不能有人为的定义域限制，否则该方 法失效.

　　在高中数学教学和学习过程中要注重一题多 解，因为一题多解能很有效地拓宽师生的解题思路， 帮助实现发散性思维能力和解题水平的提高.一题 多解思路的运用，不但能让学生掌握通性通法，而且 能让学生在横向、纵向、广度、深度等多个角度认识 到各知识板块之间的联系，在经验积累的过程中不 断提高解决问题的能力，从而在处理各种问题时信 手拈来，游刃有余.

　参考文献 :

　　[1] 豆妮娟.浅析从一题多解谈高中数学的发散思维 [J]. 中国科教创新导刊，2014 (09 ) : 161 -162.

　　[2] 曹亚奇.利用柯西不等式求最值问题中的易错点剖析 [J]. 中学生数理化 ( 高考数 学) ，2022 (06) : 28-29.